数据挖掘常见面试题

1.机器学习方面

1.1 为什么会有过拟合，如何预防或克服过拟合？

过拟合(overfit)： 在训练数据集上能获得很好的拟合，但在测试数据集上拟合的很糟糕，这种现象叫过拟合，就是训练的模型过于记住了训练样本的特征，使模型的训练误差很小，泛化误差很大。
过拟合产生的原因：
1.训练集和测试集特征分布不一致
2.数据噪声太大
3.数据量太小
4.特征量太多
5.模型太过复杂
解决方法：
1.减少特征数量(人工定义留多少个feature或算法选取这些feature)
2.正则化(即Regularization，包括L1和L2，效果是减小部分feature的权重)
3.增大样本训练规模
4.简化模型
5.交叉验证(K折交叉验证)
6.dropout
为什么L2正则化项能防止过拟合？
L2正则化就是在损失函数(衡量预测值与真实值之间差异的函数)后面再加上一个正则化项：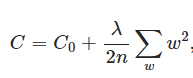
C0代表原始的损失函数，后面一项就是L2正则化项，它是所有参数w的平方和除以训练集的样本量n，λ就是正则项系数，权衡正则与C0项的比重。另外还有一个系数1/2，主要是为了后面求导的结果方便，后面那一项求导会产生一个2，与1/2相乘刚好凑整。

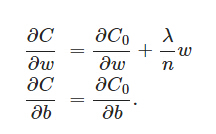
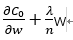可以看作权重w的斜率，η是学习率，每次以η为步长减小权重w。
可以发现L2 正则化项对b没有影响，但是对于w有影响：

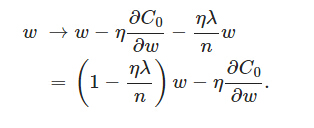
在不使用L2正则化时，求导结果中w前系数为1，现在为1−ηλ/n，因为η、λ、n都是正的，所以1−ηλ/n小于1，它的效果是减小w，这也就是权重衰减（weight decay）的由来。当然考虑到后面的导数项，w最终的值可能增大也可能减小。
另外，需要提一下，对于基于mini-batch的随机梯度下降，w和b更新的公式跟上面给出的有点不同：

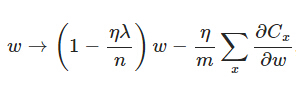
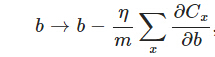
对比上面w的更新公式，可以发现后面那一项变了，变成所有导数加和，乘以η再除以m，m是一个mini-batch中样本的个数。
到目前为止，我们只是解释了L2正则化项有让w“变小”的效果，但是还没解释为什么w“变小”可以防止overfitting？一个所谓“显而易见”的解释就是：更小的权值w，从某种意义上说，表示网络的复杂度更低，对数据的拟合刚刚好（这个法则也叫做奥卡姆剃刀），而在实际应用中，也验证了这一点，L2正则化的效果往往好于未经正则化的效果。当然，对于很多人（包括我）来说，这个解释似乎不那么显而易见，所以这里添加一个稍微数学一点的解释（引自知乎）：
过拟合的时候，拟合函数的系数往往非常大，为什么？如下图所示，过拟合，就是拟合函数需要顾忌每一个点，最终形成的拟合函数波动很大。在某些很小的区间里，函数值的变化很剧烈。这就意味着函数在某些小区间里的导数值（绝对值）非常大