【贝叶斯分类器-机器学习】

贝叶斯定理

（1）先验概率（Prior Probability）：在没有训练样本数据前，根据以往经验和分析得到的概率，初始时假设样本h的初始概率，用P(h)表示。
（2）后验概率（Posterior Probability）：当下事件由因及果发生的概率，求导致该事件发生的原因是由某个因素引起的可能性的大小。由样本属性x导致分类为c的概率P(c|x)就称为后验概率。
（3）类条件概率（Class Conditional Probability）：当下事件由果及因发生的概率。样本x相对于类标签c的概率，也称为似然，记作P(x|c)。

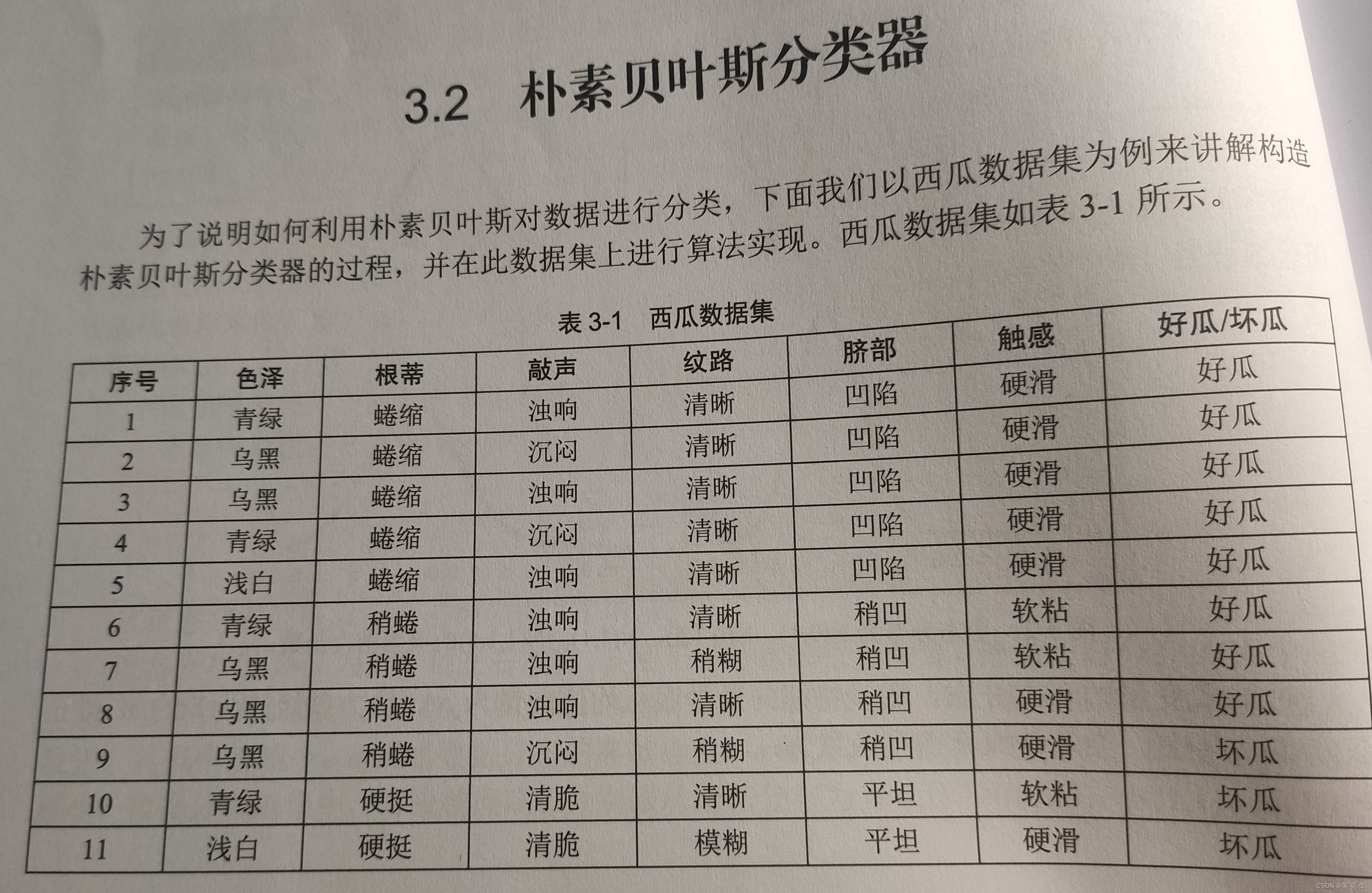
朴素贝叶斯分类器（样本数据特征相互独立）

（1）根据样本数据，求先验概率
（2）依次求每个特征的类条件概率。
（3）计算后验概率，比较。
（4）判断结果为后验概率值较大的结果。

平滑方法

在计算属性特征的条件概率时，可能会出现某属性特征在训练集中没有出现过，导致计算的概率结果为0。这显然不合理，不能因为一件事情没有观察到就武断地判断这件事件的概率为0。平滑技术就是用来解决在实际数据处理过程中出现的0概率问题，平滑处理的基本思想是“劫富济贫”，即提高低概率，降低高概率，使概率分布趋近于实际分布水平。
引入拉普拉斯平滑技术，修正后的类先验概率和类条件概率可表示为：
$$p(c)=|T|+$$