02-数据结构与算法-数组实现队列

02-数据结构与算法-数组实现队列

思路

1. 队列是一个有序列表，可以用数组或链表实现；
2. 遵循先入先出的原则，即存入队列的数据，要先取出，后存入的数据后取出

以下示意图模拟队列

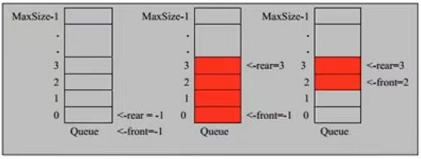
代码实现如下
数组实现队列

/**
 * 使用数组模拟队列
 */
class ArrayQueue{

    private int maxSize; //表示数组的最大容量
    private int front; //指向队列头
    private int rear;  //指向队列尾
    private int[] arr; //用于存放数据，模拟队列

    public ArrayQueue(int maxSize) {
        this.maxSize = maxSize;
        arr = new int[maxSize];
        front = -1; //指向队列头部，分析出指向队列头的前一个位置
        rear = -1;  //指向队列尾，指向队列尾部的具体数据（即队列的最后一个数据）
    }

    //判断队列是否慢
    public boolean isFull(){
        return rear == maxSize - 1;
    }

    //判断队列是否为空
    public boolean isEmpty() {
        return rear == front;
    }

    //添加数据到队列
    public void addQueue(int n) {
        //判断队列是否满
        if (isFull()) {
            System.out.println("队列已满，不能加入数据");
            return;
        }
        rear++; //让rear后移
        arr[rear] = n;
    }

    //数据出队列
    public int getQueue() {
        //判断队列是否为空
        if (isEmpty()) {
            //通过抛异常处理
            throw  new RuntimeException("队列为空，不能取数据");
        }
        front++; //取数据，front后移
        return arr[front];
    }

    //显示队列的所有数据
    public void showQueue() {
        if (isEmpty()) {
            System.out.println("队列为空，无数据！！！");
        }
        //展示队列中的所有数据，包括以取出的数据
//        for (int i = 0; i < arr.length; i++) {
//            System.out.printf("%d\t",i,arr[i]);
//        }
        //展示队列中存在的数据，剔除以取出的数据
        for (int i = front + 1; i <= rear; i++) {
            System.out.printf("%d\t",i,arr[i]);
        }
    }

    //显示队列的头数据，注意不是取出数据
    public int headQueue(){
        if (isEmpty()) {
            throw  new RuntimeException("队列为空，无数据！！！");
        }
        return arr[front + 1];
    }

}

但是当前实现队列有个问题，未实现环形数组，当数据全部取出，队列为空，无法添加数据。解决办法使用算法，改进成为环形队列。

思路

1. front变量含义做调整：front就指向队列的第一个元素，也就是说，arr[front]就是第一个元素，front的初始值默认为0；
2. rear变量含义做调整：rear指向队列的最后一个元素的后一个位置，因为希望空出一个空间作为约定，rear默认初始值为0；
3. 当队列满时，条件是(rear + 1) % maxSize = front ,队列满；
4. 当队列为空时，条件是 rear == front为空；
5. 队列中有效的数据个数为 (rear + maxSize - front) % maxSize

代码实现：

/**
 * 使用数组模拟环形队列
 * 环形队列的最大有效数据数量为 maxSize - 1
 */
class CircleArrayQueue{


    private int maxSize; //表示数组的最大容量
    private int front;   //front变量含义做调整：front就指向队列的第一个元素，也就是说，arr[front]就是第一个元素，front的初始值默认为0
    private int rear;    //rear变量含义做调整：rear指向队列的最后一个元素的后一个位置，因为希望空出一个空间作为约定，rear默认初始值为0
    private int[] arr;   //用于存放数据，模拟队列

    public CircleArrayQueue(int maxSize) {
        this.maxSize = maxSize;
        arr = new int[maxSize];
    }

    //判断队列是否满
    public boolean isFull(){
        return (rear + 1) % maxSize == front;
    }

    //判断队列是否为空
    public boolean isEmpty() {
        return rear == front;
    }

    //添加数据到队列
    public void addQueue(int n) {
        //判断队列是否满
        if (isFull()) {
            System.out.println("队列已满，不能加入数据");
            return;
        }
        //直接将数据加入即可
        arr[rear] = n;
        //将rear后移，必须考虑取模
        rear = (rear + 1 ) % maxSize;
    }

    //数据出队列
    public int getQueue() {
        //判断队列是否为空
        if (isEmpty()) {
            //通过抛异常处理
            throw  new RuntimeException("队列为空，不能取数据");
        }
        //这里需要分析，front是指向队列的第一个元素
        //1、先把front对应的值，保存到一个临时变量
        //2、将front后移,考虑取模
        //3、将临时保存的变量返回
        int tmp = arr[front];
        front = (front + 1) % maxSize;
        return tmp;
    }

    //显示队列的所有数据
    public void showQueue() {
        if (isEmpty()) {
            System.out.println("队列为空，无数据！！！");
        }
        //获取有效数据
        //从front开始遍历,siz()有效数据数量
        for (int i = front; i < front + size(); i++) {
            System.out.printf("arr[%d]=%d\n",i % maxSize,arr[i % maxSize]);
        }
    }

    //取出当前队列有效数据个数
    public int size() {
        return (rear + maxSize - front) % maxSize;
    }

    //显示队列的头数据，注意不是取出数据
    public int headQueue(){
        if (isEmpty()) {
            throw  new RuntimeException("队列为空，无数据！！！");
        }
        return arr[front];
    }

}

注意：环形队列最大有效数量为 max -1, 队列总会空出一个空间出来。