吴恩达深度学习 5.1 序列模型-循环神经网络

最新推荐文章于 2023-09-11 23:50:58 发布

垚焱焱

最新推荐文章于 2023-09-11 23:50:58 发布

阅读量1.4k

点赞数 1

文章标签：深度学习 rnn 神经网络

本文链接：https://blog.youkuaiyun.com/weixin_43638099/article/details/121758431

版权

1. 知识点：

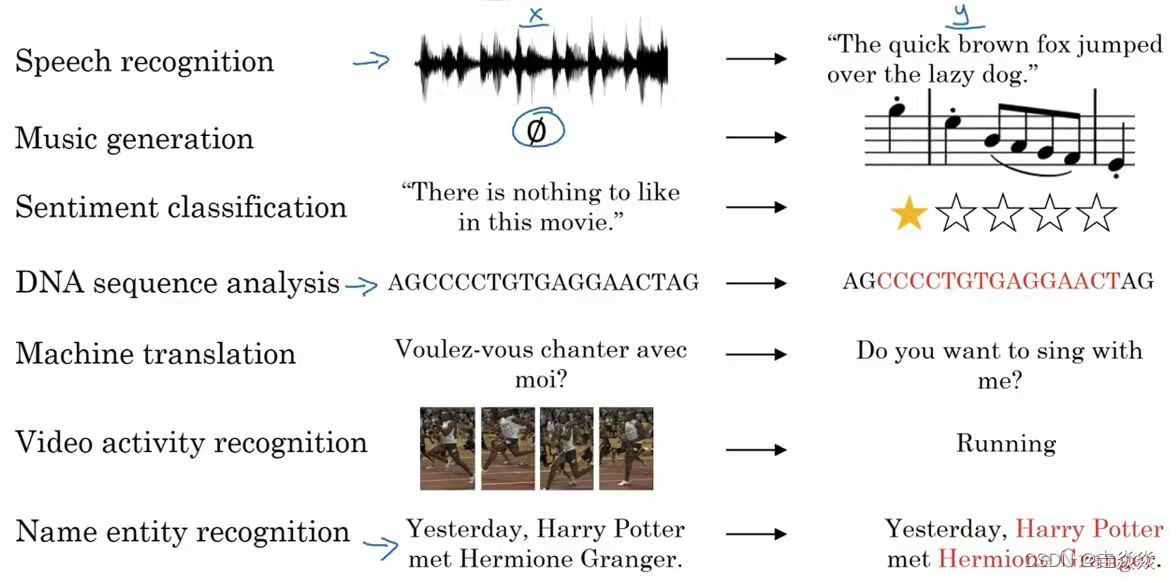
序列模型的应用：

语音识别：输入的语音和输出的文本，都是序列数据。

音乐生成：生成的音乐乐谱是序列数据。

情感分类：将输入的评论转换为相应的评价等级。输入是序列。

机器翻译：两种不同语言之间的转换。输入和输出都是序列。

视频行为识别：识别输入的视频帧序列中的人物行为。

命名实体识别：从输入的句子中识别实体的名字。

符号定义：

输入x：输入序列，如，“A snow year,a rich year”。 $x^{<t>}$ 表示输入序列x中的第t个符号。

输出y：输出序列，如，“10001010”。 $y^{<t>}$ 表示输出序列y中的第t个符号。

Tx表示输入x的长度。

Ty表示输出y的长度。

$x^{(i)<t>}$ 表示第i个输入样本的第t个符号。

用每个单词的编码（如one-hot编码）表示第一个输入符号：可以实现输入x到输出y的转换。

传统神经网络：将输入序列X进行编码（比如one-hot编码），输入到多层神经网络中，得出输出Y

存在的问题：

1)对于不同的例子输入序列编码的长度不同

2)不能共享从文本不同位置学习到的特征（没咋看明白？？？）

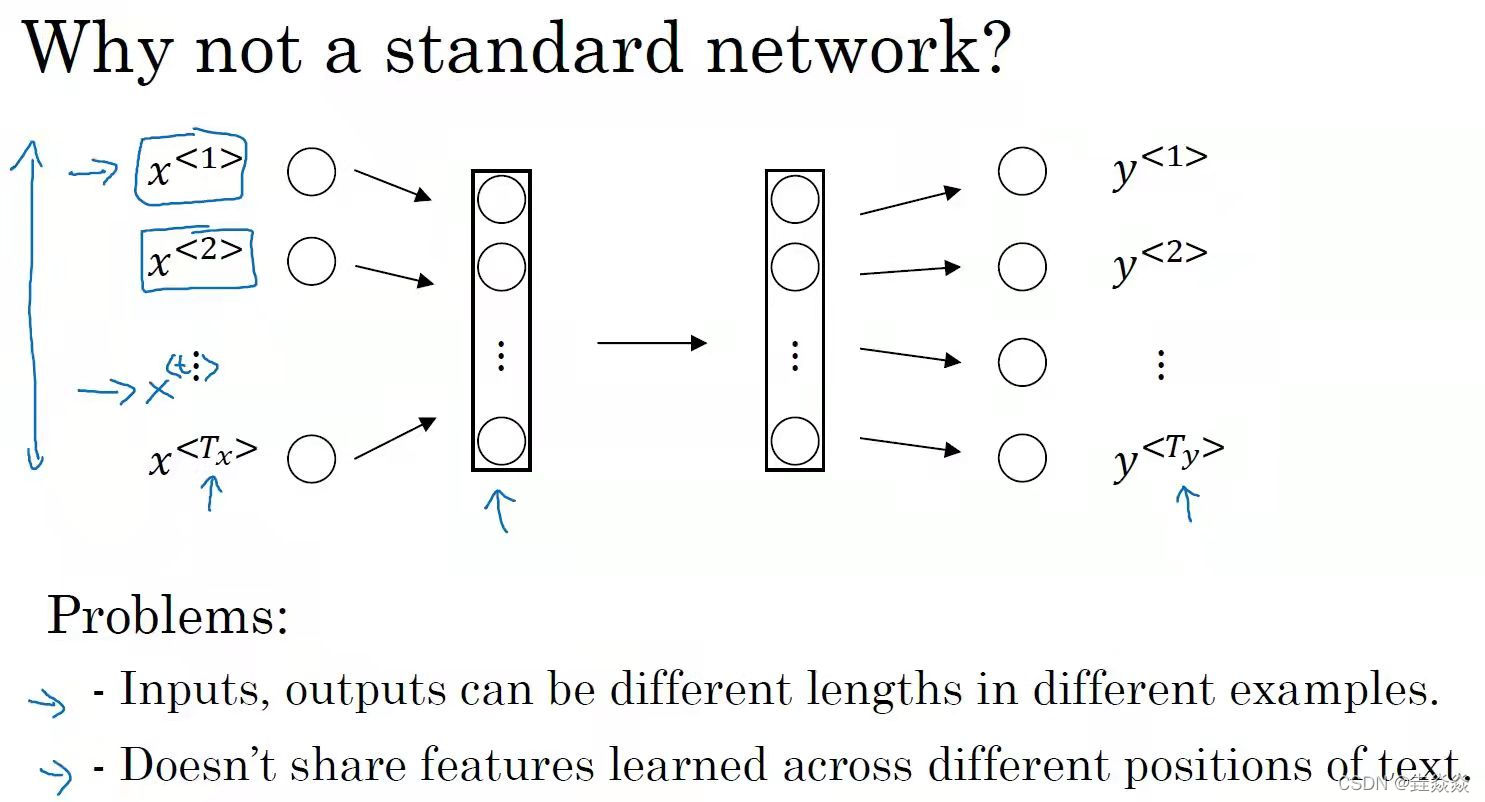
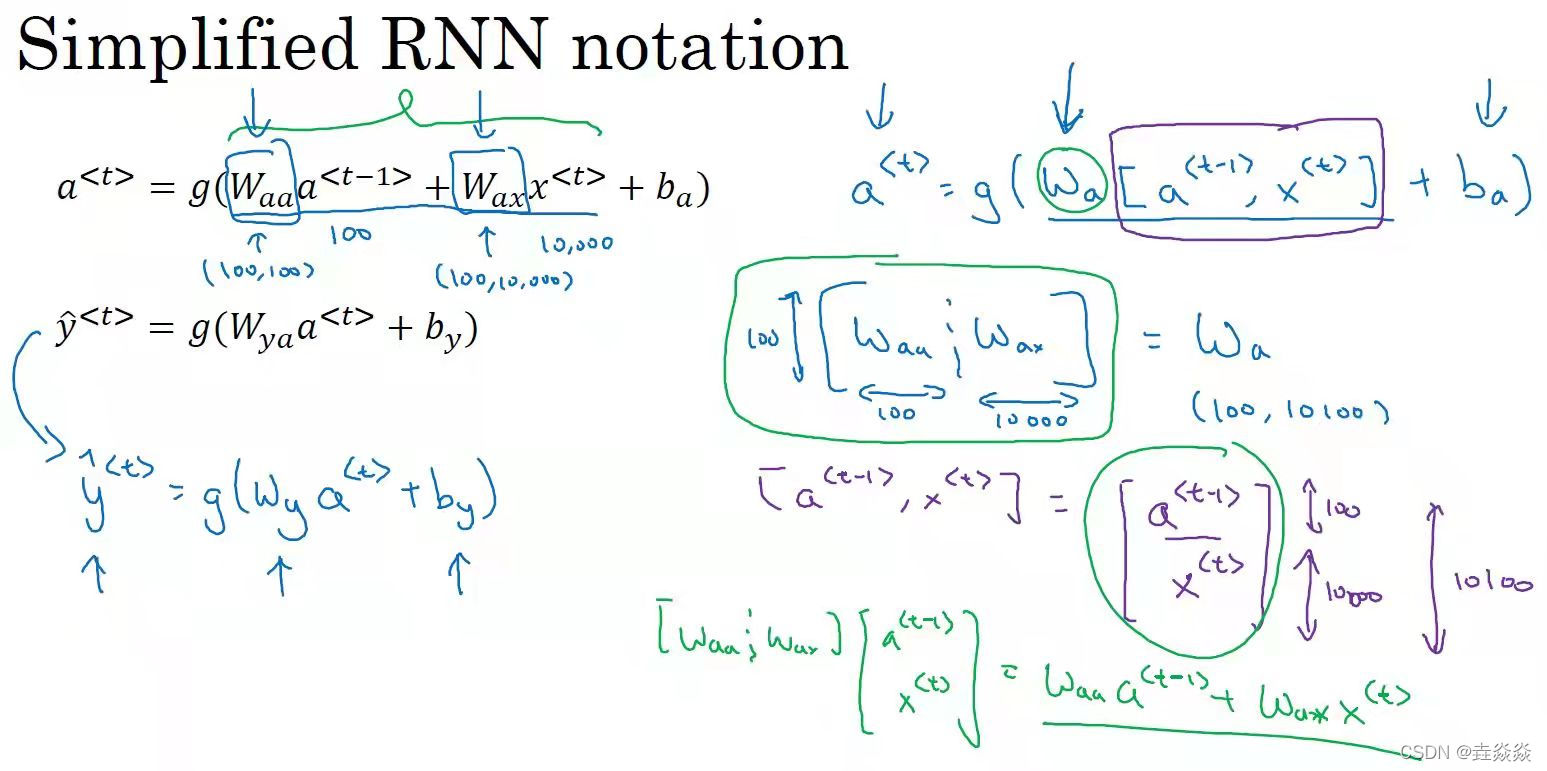
循环神经网络：

每个单元有两个输出：1个输入序列元素 $y^{<t>}$ ，和1个激活值。

每个单元共享参数： $W_{aa}$ ， $W_{ax}$ ， $W_{ya}$ 。

激活值实现输出序列元素 $y^{<t>}$ 使用了从开始到当前的所有输入序列元素。

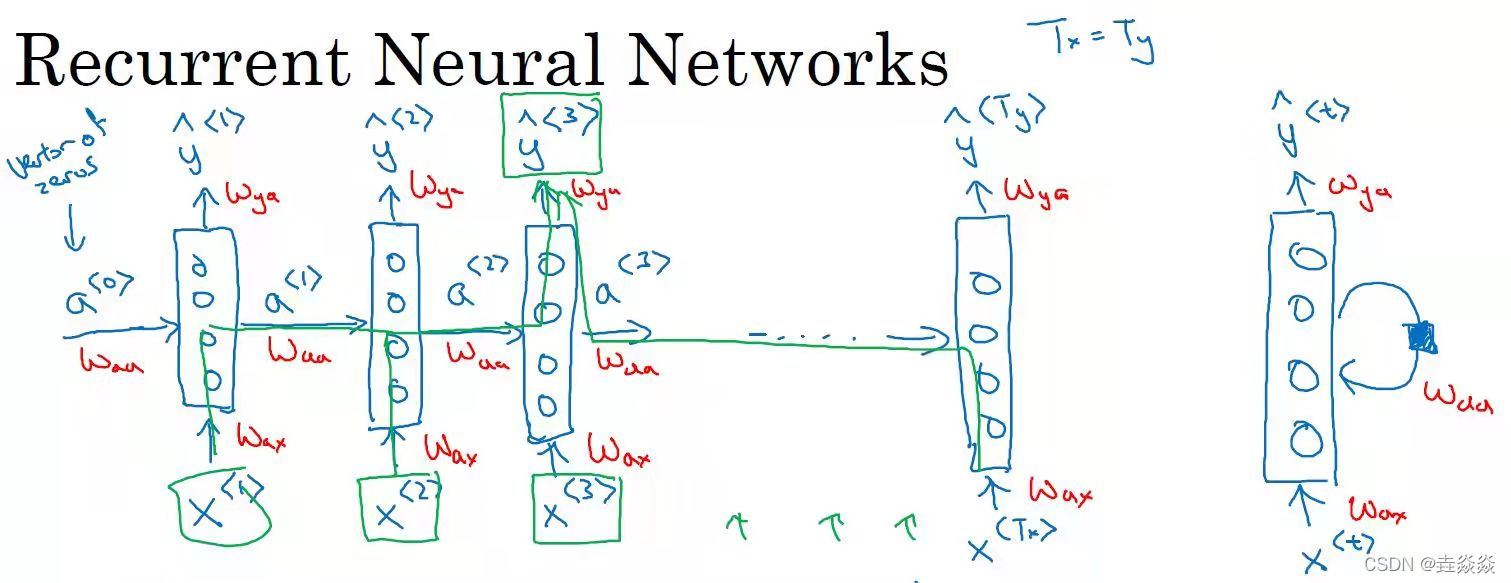
循环神经网络的前向传播：

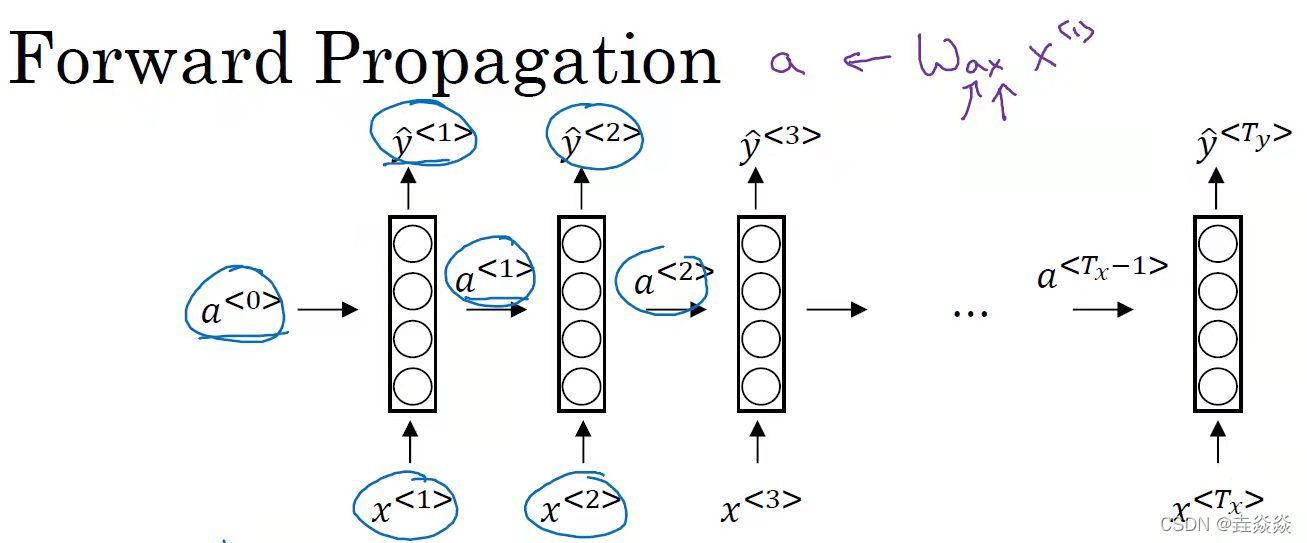
循环神经网络的后向传播和损失函数：

损失函数： $L^{<t>}(\widehat{y}^{<t>},y^{<t>})=-y^{<t>}log\widehat{y}^{<t>}-(1-y^{<t>})log(1-\widehat{y}^{<t>})$ , $L(\widehat{y},y)=\sum_{t=1}^{Ty}L^{<t>}(\widehat{y}^{<t>},y^{<t>})$

反向传播：按照前向传播相反的方向进行导数计算

不同类型的RNN：

输入和输出长度相等：

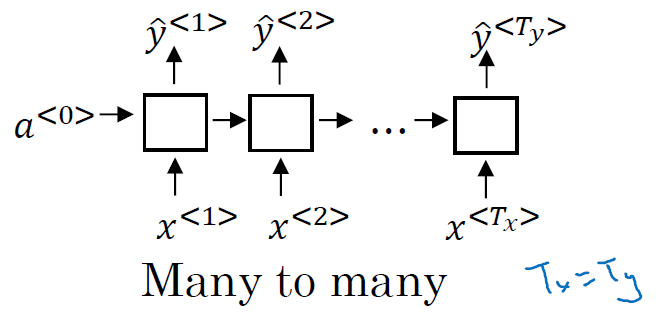
preview

多个输入元素和一个输出元素：比如，情感分类

preview

一个输入元素和多个输出元素：比如，音乐生成，输入一个音乐类型，生成音乐序列

preview

多个输入元素和多个输出元素，输入和输出长度不等：比如，机器翻译

preview

语言模型：评估句子中各个单词出现的可能性，进而评估整个句子出现的可能性。

preview

RNN语言模型：

向量化：将句子中的单词使用字典进行向量化

输入：零向量+样本输入序列

标签：样本输入序列+结束元素

第一步：用零向量，对输出进行预测，即预测第一个单词

后面步骤：用前面的隐藏输入a和当前输入x，预测后面一个单词是某个单词的概率

preview

新序列采样：简单测试一个模型的学习效果

第一步： $x^{<0>}=0,a^{<0>}=0$ ，计算第一个输出单词 $\widehat{y}^{<1>}$ 。

后面步骤：将 $\widehat{y}^{<1>}$ 作为下一个时间步的输入，预测下一个输出。

也有基于字符的语言模型：

preview

RNN模型中不擅长捕获长期依赖总是：很难捕获前面的单词对后面远距离单词产生的影响

preview

RNN的GRU单元：

记忆单元候选 $\widetilde{c}^{<t>}$ 当前值由记忆单元前一个值和输入当前值计算得出。

更新门 $\Gamma _{u}$ 由记忆单元前一个值和输入当前值计算得出，经sigmoid()运算，值在0~1之间。

记忆单元 $c^{<t>}$ 当前值由更新门、记忆单元候选值、记忆单元前一个值运算得出。这样可以通过更新门的作用给输入较大的权重。

preview

LSTM：在RNN的基础上增加了遗忘门和输出门，用更新门和遗忘门计算记忆单元，用输出门计算输出

preview

双向RNN：

单向RNN不能利用未来信息对当前信息进行预测

preview

双向RNN：有前向连接层和反向连接层

preview

深层RNN：对于RNN来说，三层神经网络已经很多了

preview

2. 应用实例：

实现思路：

RNN的单步前向传播：

输入1：序列xt，维度为（n_x，m），即（输入单词（或字符）的向量长度，样本数）。
输入2：参量向量
输入3：隐藏状态a_prev,维度为（n_a,m），即（隐藏状态的向量长度，样本数）。
计算1：隐藏状态a=Waa*a_prev+Wax*xt+ba。
计算2：预测值 yt=softmax(Wya*a+by)
输出：预测值yt，隐藏状态a，参数。

RNN前向传播：

输入：x，维度为（n_x，m，T_x）,即（输入单词（或字符）的向量长度，样本数，时间步数）
计算：依次用单步前向传播方法对每个时间步t的输入数据x[：，：，t]进行计算。

LSTM单元前向传播：

输入：x_t（时间步t的输入数据），a_prev(隐藏状态)，c_prev(记忆状态)，参数
计算1：遗忘门，ft=sigmoid(Wf*(a_prev,x_t)+bf)。
计算2：更新门，it=sigmoid(Wi*(a_prev,x_t)+bi)。
计算3：更新单元，cct=tanl(Wc*(a_prev,x_t)+bc)。
计算4：记忆状态，c=ft*c_prev+it*cct。
计算5：输出门，t=sigmoid(Wo*(a_prev,x_t)+bo)。
计算6：隐藏状态，a=ot*tanl(c)。
计算7：预测值，yt=softmax(Wy*a+by)。

LSTM前向传播：

用LSTM单元前向传播对每个时间步t的输入数据进行运算。

根据恐龙名字的数据集，生成新的恐龙名字。

搭建优化模型：
RNN前向传播。
RNN反向传播。
梯度修剪。
更新参数。

训练模型：
给写恐龙名字的数据集作为输入样本和标签。输入样本第一个时间步x1为零向时，标签的最后一个时间步yt为结束符。
对输入和标签，用优化模型进行迭代，更新参数。

用训练好的模型生成恐龙名字：
对第一个时间步的输入x1和隐藏状态a0,初始化为零向量。
用训练好的模型计算a1,y1。
用x2=y1,和a1作为输入，计算a2和y2。
依次，直到生成结束符，或者时间步已超过阈值。

import numpy as np
import rnn_utils

def rnn_cell_forward(xt, a_prev, parameters):
    """
    根据图2实现RNN单元的单步前向传播
    
    参数：
        xt -- 时间步“t”输入的数据，维度为（n_x, m）
        a_prev -- 时间步“t - 1”的隐藏隐藏状态，维度为（n_a, m）
        parameters -- 字典，包含了以下内容:
                        Wax -- 矩阵，输入乘以权重，维度为（n_a, n_x）
                        Waa -- 矩阵，隐藏状态乘以权重，维度为（n_a, n_a）
                        Wya -- 矩阵，隐藏状态与输出相关的权重矩阵，维度为（n_y, n_a）
                        ba  -- 偏置，维度为（n_a, 1）
                        by  -- 偏置，隐藏状态与输出相关的偏置，维度为（n_y, 1）
    
    返回：
        a_next -- 下一个隐藏状态，维度为（n_a， m）
        yt_pred -- 在时间步“t”的预测，维度为（n_y， m）
        cache -- 反向传播需要的元组，包含了(a_next, a_prev, xt, parameters)
    """
    
    # 从“parameters”获取参数
    Wax = parameters["Wax"]
    Waa = parameters["Waa"]
    Wya = parameters["Wya"]
    ba = parameters["ba"]
    by = parameters["by"]
    
    # 使用上面的公式计算下一个激活值
    a_next = np.tanh(np.dot(Waa, a_prev) + np.dot(Wax, xt) + ba)
    
    # 使用上面的公式计算当前单元的输出
    yt_pred = rnn_utils.softmax(np.dot(Wya, a_next) + by)
    
    # 保存反向传播需要的值
    cache = (a_next, a_prev, xt, parameters)
    
    return a_next, yt_pred, cache

np.random.seed(1)
xt = np.random.randn(3,10)
a_prev = np.random.randn(5,10)
Waa = np.random.randn(5,5)
Wax = np.random.randn(5,3)
Wya = np.random.randn(2,5)
ba = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {"Waa": Waa, "Wax": Wax, "Wya": Wya, "ba": ba, "by": by}

a_next, yt_pred, cache = rnn_cell_forward(xt, a_prev, parameters)
print("a_next[4] = ", a_next[4])
print("a_next.shape = ", a_next.shape)
print("yt_pred[1] =", yt_pred[1])
print("yt_pred.shape = ", yt_pred.shape)

a_next[4] =  [ 0.59584544  0.18141802  0.61311866  0.99808218  0.85016201  0.99980978
 -0.18887155  0.99815551  0.6531151   0.82872037]
a_next.shape =  (5, 10)
yt_pred[1] = [0.9888161  0.01682021 0.21140899 0.36817467 0.98988387 0.88945212
 0.36920224 0.9966312  0.9982559  0.17746526]
yt_pred.shape =  (2, 10)

def rnn_forward(x, a0, parameters):
    """
    根据图3来实现循环神经网络的前向传播
    
    参数：
        x -- 输入的全部数据，维度为(n_x, m, T_x)
        a0 -- 初始化隐藏状态，维度为 (n_a, m)
        parameters -- 字典，包含了以下内容:
                        Wax -- 矩阵，输入乘以权重，维度为（n_a, n_x）
                        Waa -- 矩阵，隐藏状态乘以权重，维度为（n_a, n_a）
                        Wya -- 矩阵，隐藏状态与输出相关的权重矩阵，维度为（n_y, n_a）
                        ba  -- 偏置，维度为（n_a, 1）
                        by  -- 偏置，隐藏状态与输出相关的偏置，维度为（n_y, 1）
    
    返回：
        a -- 所有时间步的隐藏状态，维度为(n_a, m, T_x)
        y_pred -- 所有时间步的预测，维度为(n_y, m, T_x)
        caches -- 为反向传播的保存的元组，维度为（【列表类型】cache, x)）
    """
    
    # 初始化“caches”，它将以列表类型包含所有的cache
    caches = []
    
    # 获取 x 与 Wya 的维度信息
    n_x, m, T_x = x.shape
    n_y, n_a = parameters["Wya"].shape
    
    # 使用0来初始化“a” 与“y”
    a = np.zeros([n_a, m, T_x])
    y_pred = np.zeros([n_y, m, T_x])
    
    # 初始化“next”
    a_next = a0
    
    # 遍历所有时间步
    for t in range(T_x):
        ## 1.使用rnn_cell_forward函数来更新“next”隐藏状态与cache。
        a_next, yt_pred, cache = rnn_cell_forward(x[:, :, t], a_next, parameters)
        
        ## 2.使用 a 来保存“next”隐藏状态（第 t ）个位置。
        a[:, :, t] = a_next

最低0.47元/天解锁文章