线性回归原理总结

结合ng的机器学习课程–线性回归部分，整理了如下的笔记，包括：线性回归模型、假设函数、代价函数、梯度下降应用于线性回归、正规方程求解、多项式回归等知识点，以及各部分的代码实现。

不基于sklearn，纯用numpy和pandas来实现的线性回归，可以查看吴恩达老师机器学习课程的课后作业。

---

目录
1、线性回归问题描述
2、代价函数
3、梯度下降
4、梯度下降应用于线性回归，以及向量化
5、正规方程
6、回归的性能评估
7、基于sklearn的两种实现
8、多项式回归

---

1、线性回归问题描述

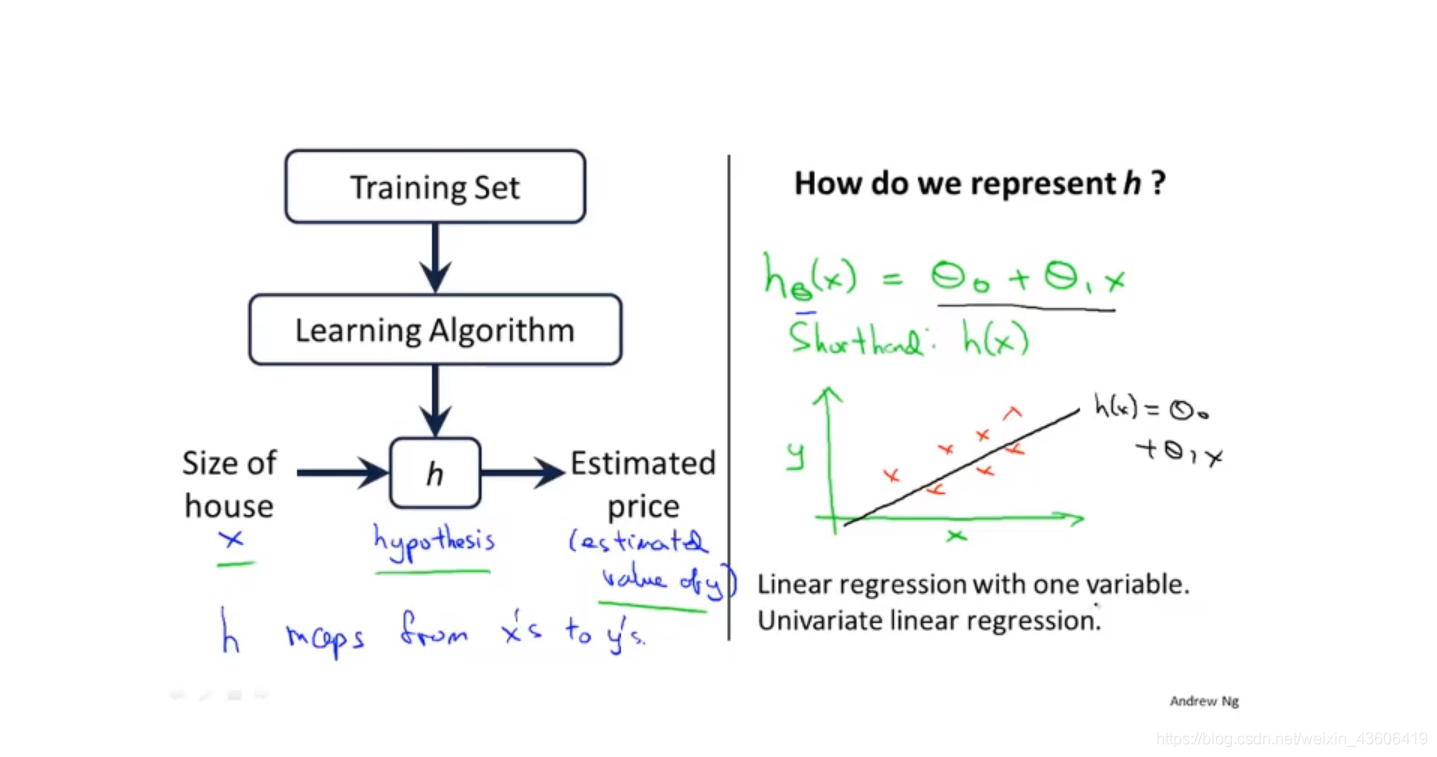
拿房价预测为例，为了简化只考虑一个特征（房子的尺寸），因变量为(房价)。观察数据集，我们可以发现y和x近似为线性关系，于是得到如图的假设函数。之后，使用学习算法（梯度下降/正规方程）得到参数的最优解，以预测新的样本。

2、代价函数

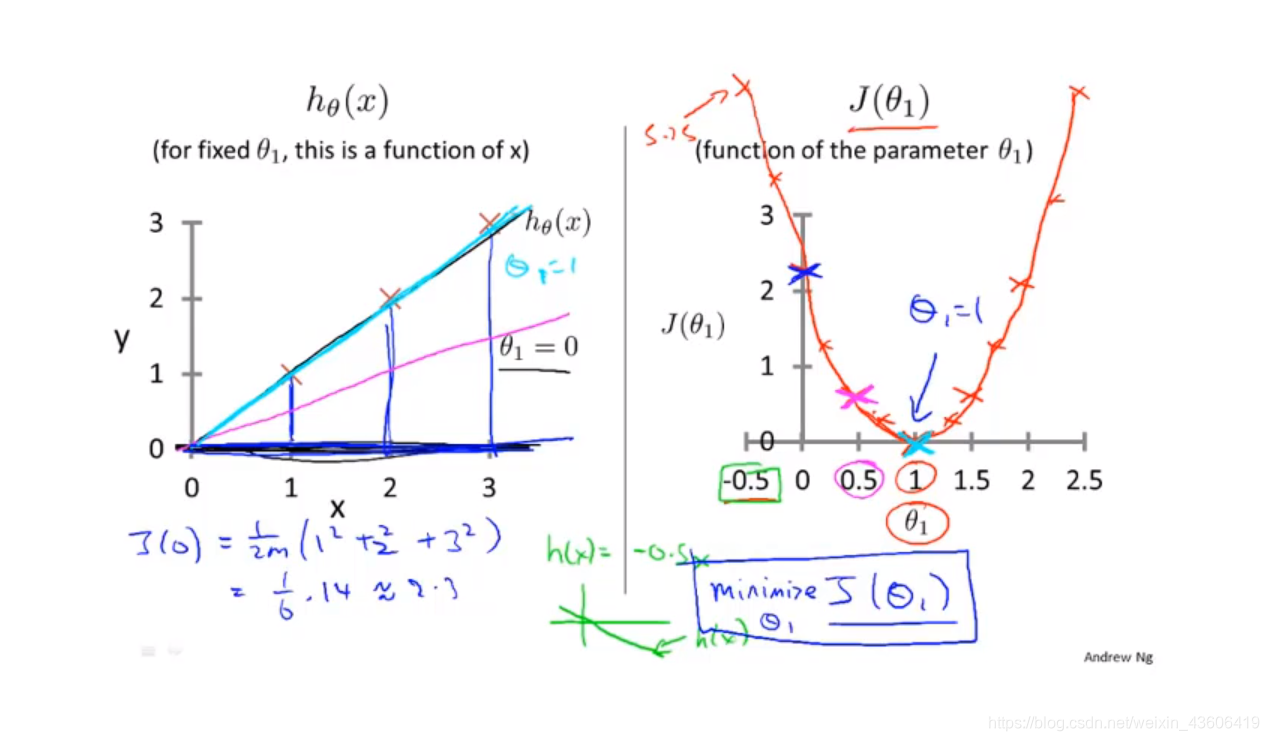
如下图所示，首先把theta0 忽略，假设我们有三个样本，然后我们取三个不同的theta1的值，分别为 0、0.5、1，然后带入代价函数表达式中，我们可以得到右边的代价函数的图像。很明显，对于此例，theta1 = 1时，代价函数达到最小值，此时theta1 为最优解。

代码片段

import numpy as np
def computeCost(X, y, theta):
    inner = np.power(((X * theta.T) -  y), 2)
    return np.sum(inner) / (2 * len(X))

3、梯度下降

在数学中，我们知道想要求解方程的最小值或者极小值，需要对方程求导，令其导数等于0，从而求解出最小值或者极小值对应的位置。
梯度下降是一个迭代过程，想象你在山顶想要下山，每一次都要寻找最快的下降方向，最后达到最低点，这个过程包含一个超参数学习率，也就是每次下降的步幅。
（注意：所有参数同时更新）

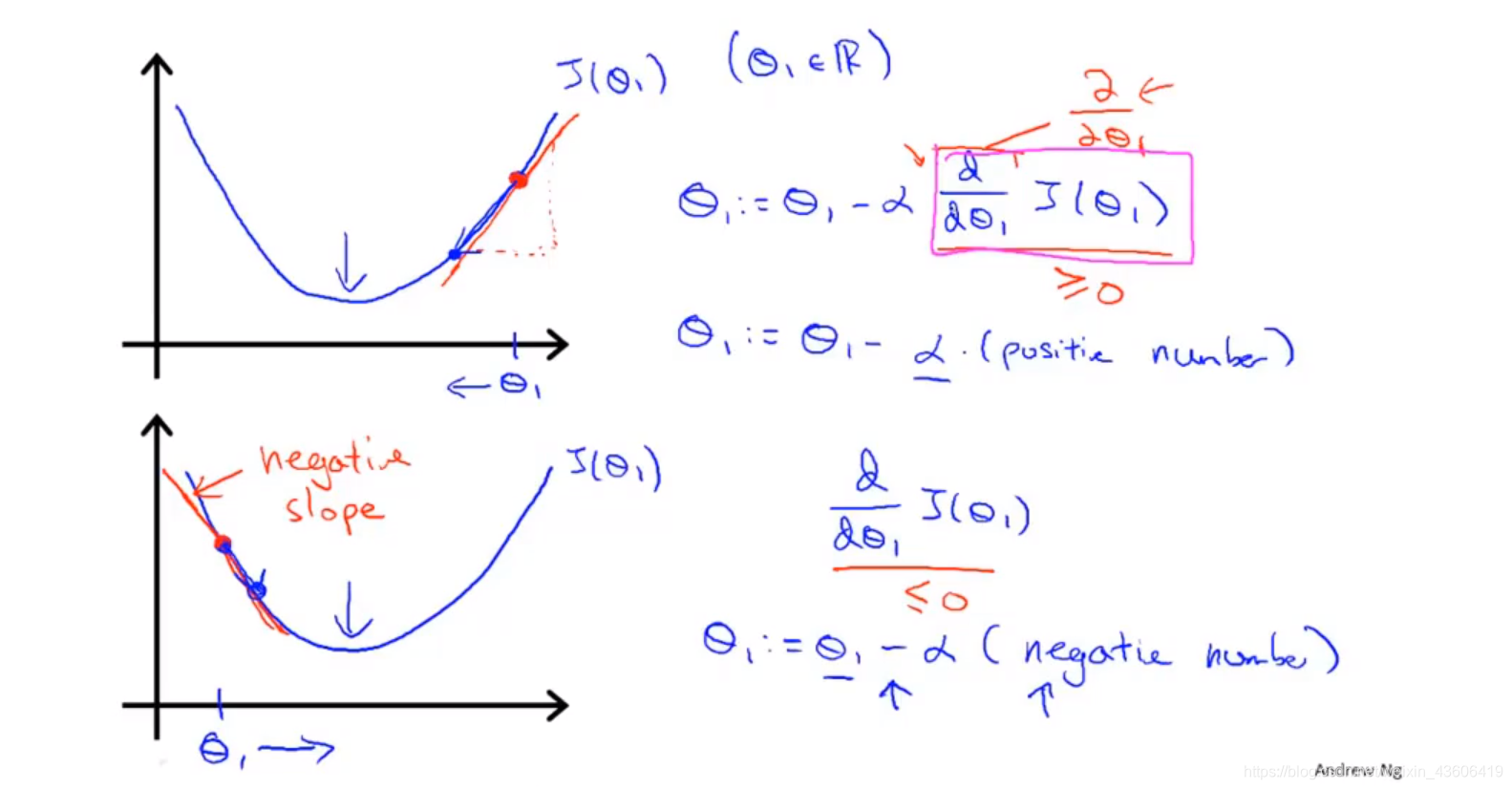
学习率为一个很小的正数，如下图所示，分别对应了偏导为正和为负的情况，也就解释了参数是在不断迭代下降的，最终到达最低点。

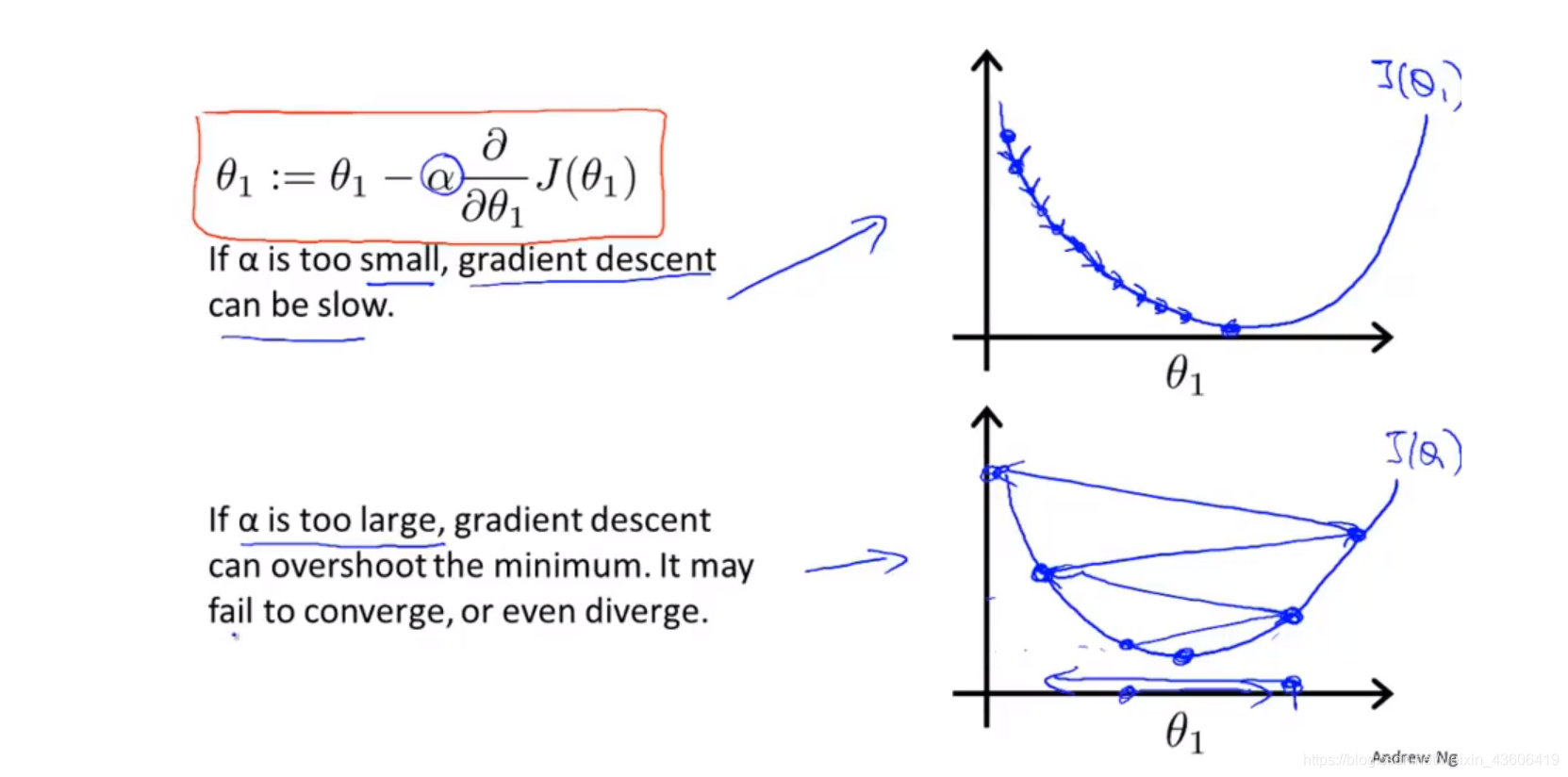
学习率的选择情况，如下图所示。

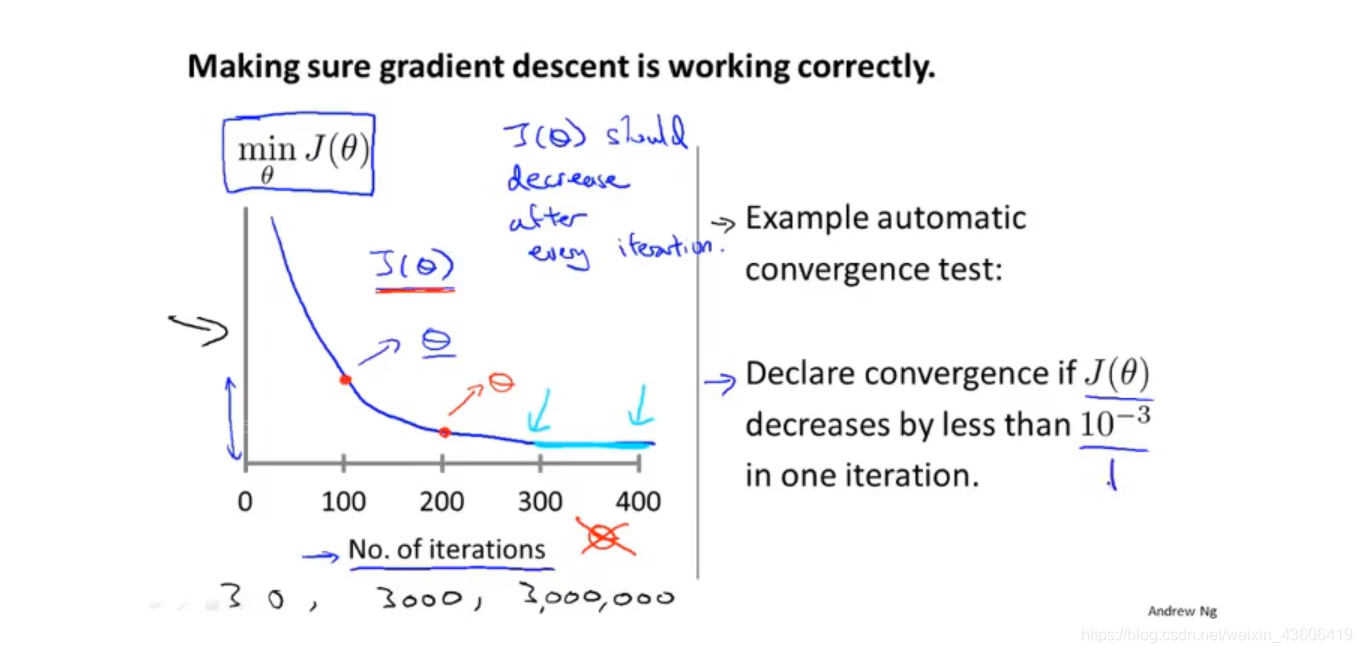
确保梯度下降正常工作，通过这样一个横坐标为迭代次数的图像，我们可以观察在迭代过程中，代价函数是不是在一直降低，以此判断是否出现异常，从而进行完善。

4、梯度下降应用于线性回归

把线性回归的代价函数带入梯度下降算法中，得到如图的表达式，需要了解偏导和链式求导的数学知识。

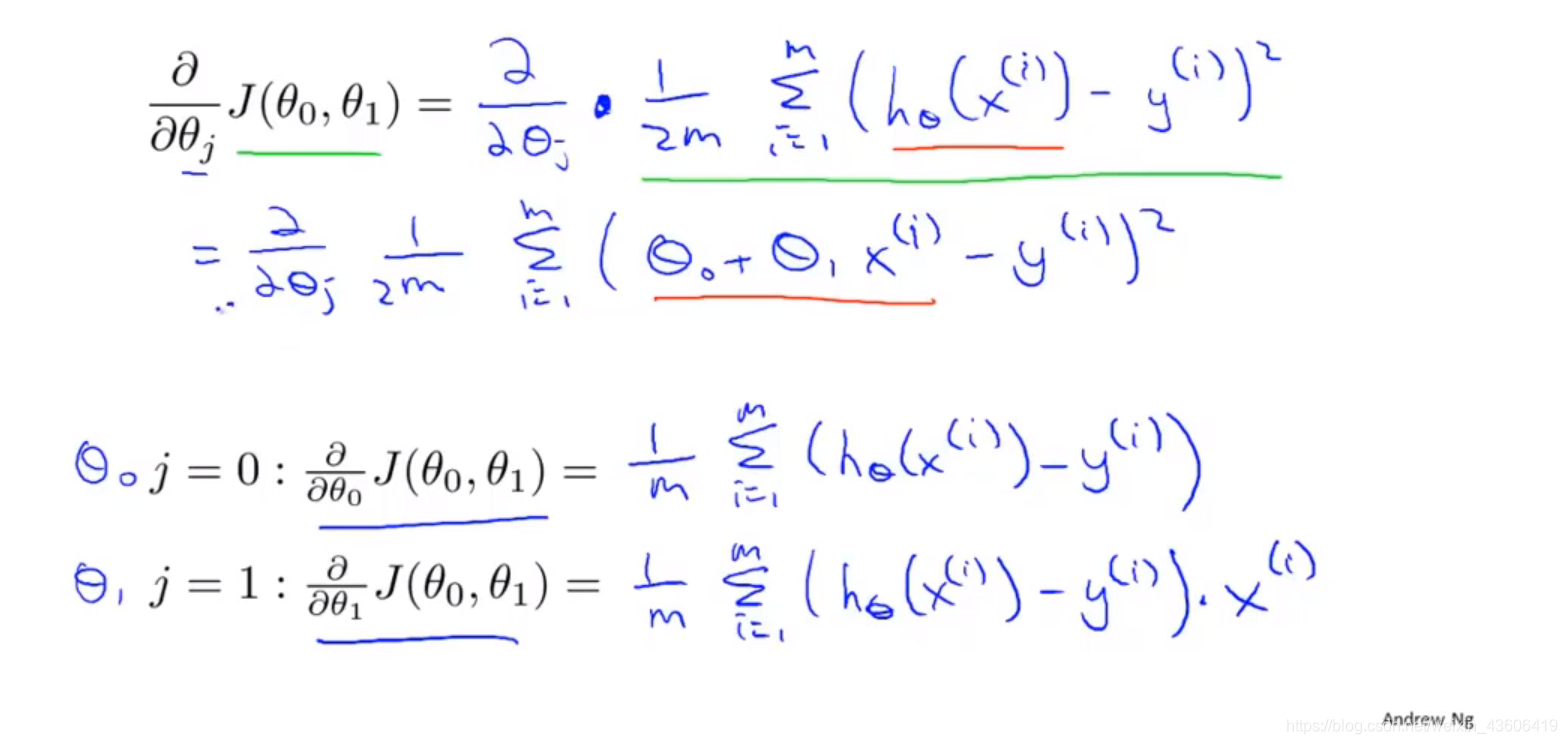
向量化的实现：
（1）假设函数的向量化

(2)代价函数的向量化

（3）梯度下降的向量化

（4）汇总

5、正规方程

另外一种，直接计算线性回归最优参数的方法，叫做正规方程。
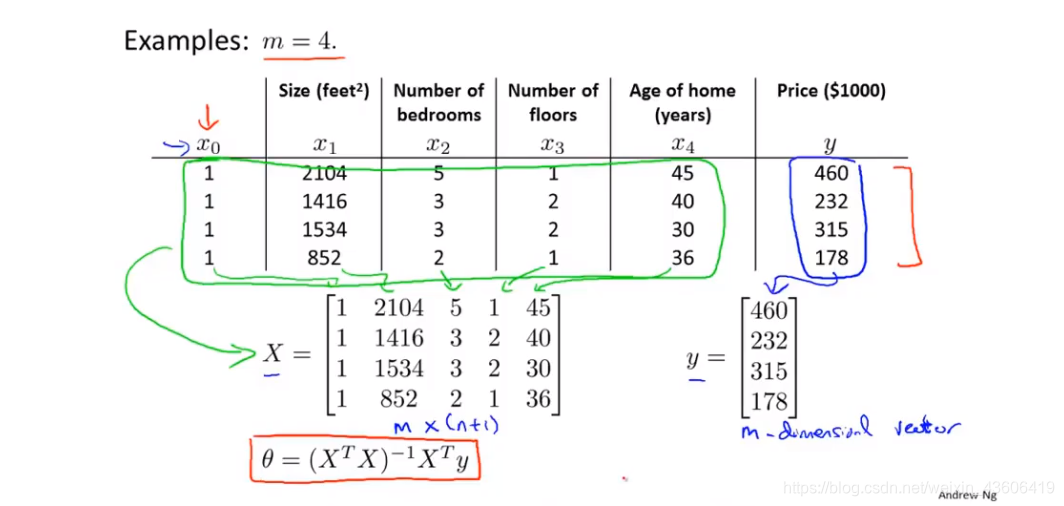
如图所示，4个样本，5个特征（包含x0），通过向量化操作，可以直接利用公式得到线性回归的最优解。

6、回归性能评估

评估原理：

基于sklearn的API

7、基于sklearn的实现

线性回归的两种API

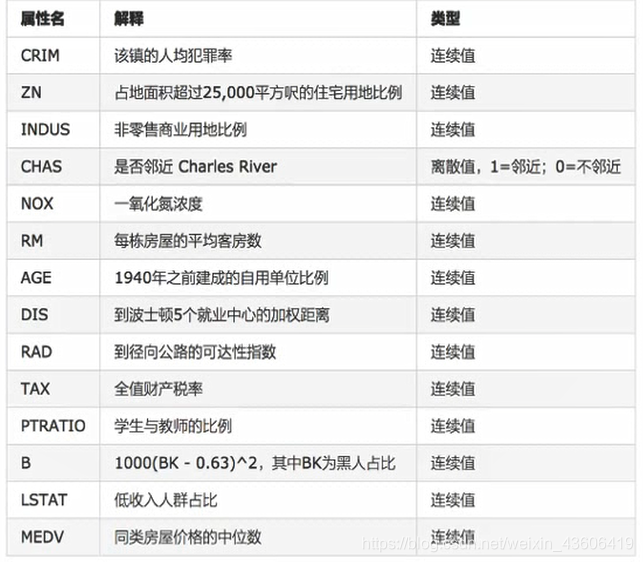
本例，我们使用sklearn封装好的波士顿房价数据集。下图为预测房价的特征。

完整代码如下

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression, SGDRegressor
from sklearn.metrics import mean_squared_error

# 加载数据集
bt = load_boston()

print(bt.data.shape)  # (506, 13) 506个样本，13个特征
print(bt.target.shape)  # (506,)

# 划分训练集、预测集
x_train, x_test, y_train, y_test = train_test_split(bt.data, bt.target, test_size=1/4)

# 数据标准化
sta_x = StandardScaler()
x_train = sta_x.fit_transform(x_train)
x_test = sta_x.transform(x_test)

# 标签标准化
sta_y = StandardScaler()
y_train = sta_y.fit_transform(y_train.reshape(-1, 1))
y_test = sta_y.transform(y_test.reshape(-1, 1))
print(y_train.shape)  # (379, 1)
print(y_test.shape)  # (127, 1)

# 正规方程优化
lr = LinearRegression()
lr.fit(x_train, y_train)

# 打印优化好的参数
print(lr.coef_)

# 转化为标准化之前的数据
y_lr_prediction = sta_y.inverse_transform(lr.predict(x_test))
print('正规方程优化，测试集每个样本预测的结果为：', y_lr_prediction)

# 回归常用的评估指标
print('正规方程的均方误差', mean_squared_error(sta_y.inverse_transform(y_test), y_lr_prediction))


# 梯度下降优化
sgd = SGDRegressor()
sgd.fit(x_train, y_train)

# 打印优化好的参数
print(sgd.coef_)

y_sgd_prediction = sta_y.inverse_transform(sgd.predict(x_test))
print('梯度下降优化，测试集每个样本预测的结果为：', y_sgd_prediction)

print('梯度下降的均方误差', mean_squared_error(sta_y.inverse_transform(y_test), y_sgd_prediction))

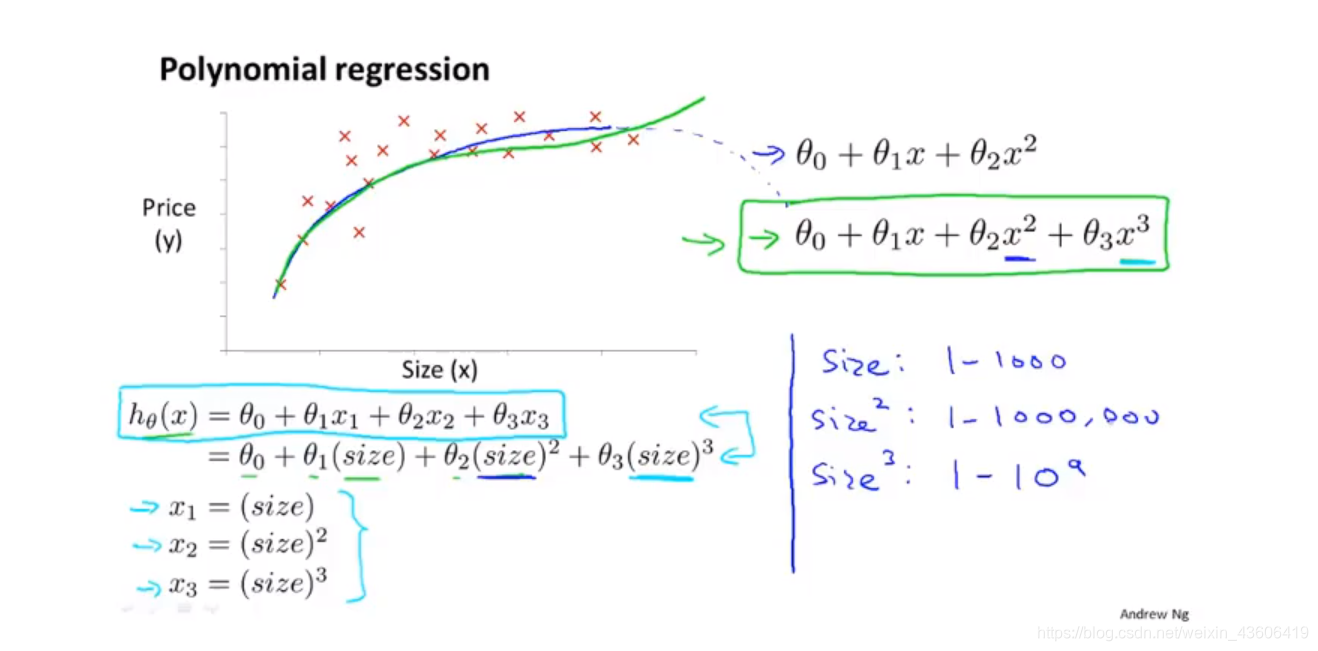
8、多项式回归

根据数据集的分布，我们可以选择不同的假设函数，下图中以 2次方 和3次方多项式为例，我们可以选择特征1（尺寸）、特征2（尺寸的平方）、特征3（尺寸的立方），进而把模型转换成线性回归。

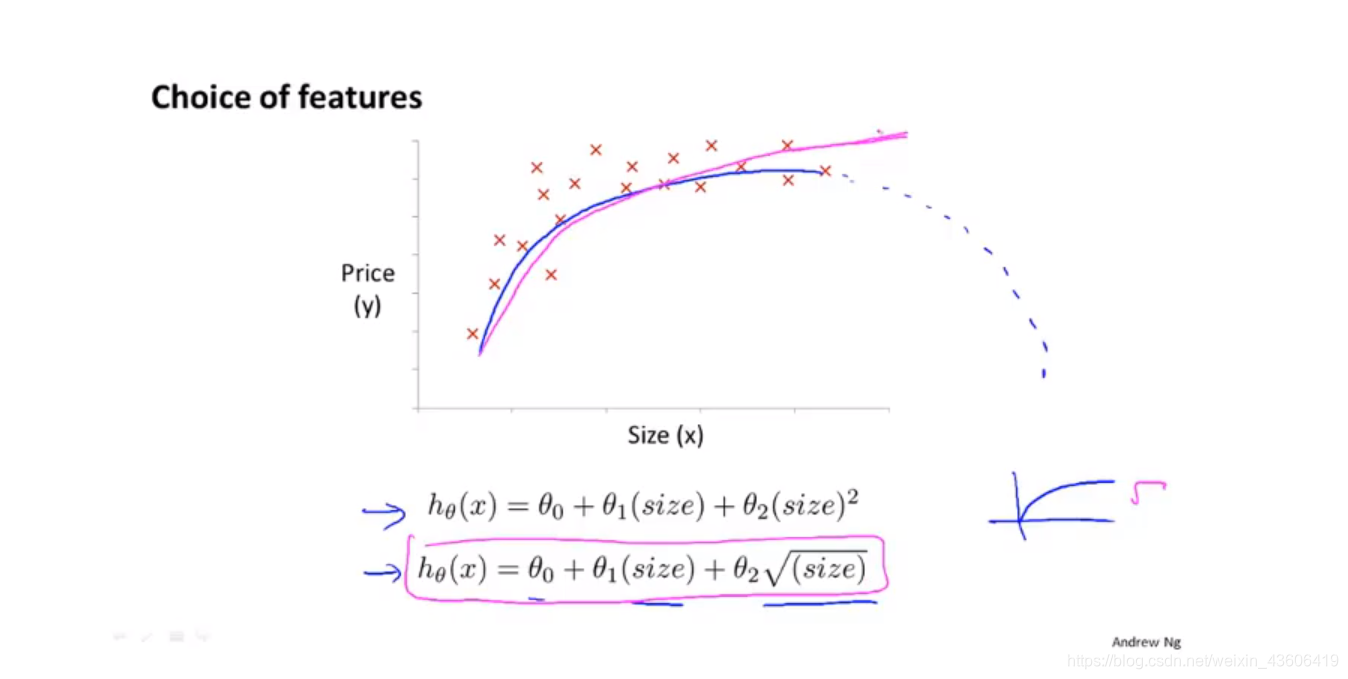
基于这个例子，还是选择特征（尺寸的平方根）较为合理。