DBscan算法理论知识

前言

本期将介绍另一种聚类算法，那就是基于密度聚类的算法。该算法的最大优点是可以将非球形簇实现恰到好处的聚类，如下图所示，即为一个非球形的典型图形：

如上图所示，右上角的样本点为一个簇，呈现球形特征，但是左下角的两个样本簇，存在交合状态，并非球形分布。如果直接使用K均值聚类算法，将图形中的数据，聚为三类，将会形成下图的效果：

如上图所示，K均值聚类的效果很显然存在差错。如果利用本文所接受的DBSCAN聚类算法，将不会出现这样的问题。不妨先将DBSCAN的聚类效果呈现在下图：

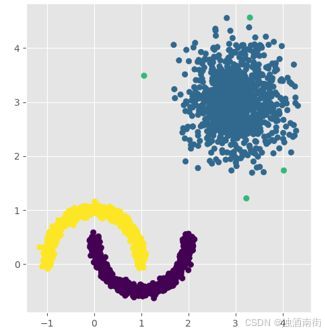
总结：Kmeans聚类存在两个致命缺点，一是聚类效果容易受到异常样本点的影响；二是该算法无法准确地将非球形样本进行合理的聚类。
基于密度的聚类则可以解决非球形簇的问题，“密度”可以理解为样本点的紧密程度，如果在指定的半径领域内，实际样本量超过给定的最小样本量阈值，则认为是密度高的对象，就可以聚成一个簇。

密度聚类的几个概念

点的$ϵ$领域:在某点p处，给定其半径e后，所得到的覆盖区域

核心对象：对于给定的最少样本量Minpts而言，如果某点p的e领域至少包含Minpts个样本点，则点p就是核心对象；

直接密度可达：假设点p为核心对象，且在点p的e领域存在点q,则从点p出发到点q是直接密度可达的。

密度可达：假设存在一系列的对象链$p_1$,$p_2$,…$p_n$,如果p_i是关于半径e和最少样本点Minpts的直接密度可达$p_{i+}$(i=1,i=2,…n),则$p_1$密度可达

密度连接：假设点o为核心对象，从点o出发得到两个密度可达点p和点q,则称点p和点q是密度相连的

聚类的簇：簇包含了最大的密度相连所构成的样本点

边界点：假设点p为核心对象，在其领域内包含了点b,如果b为非核心对象，则称其为点p的边界点。

异常点：不属于任何簇的样本点

为了更好的理解上面的概念，以及它们之间的差异，可以参考下面的图片：

如上图所示，如果$\epsilon$3，MinPts为7，则点p为核心对象（因为在其领域内至少包含了7个样本点）；点q为非核心对象；点m为点p的直接密度可达（因为它在点p的$\epsilon$领域内）。

如上图所示，如果$ϵ$为3，MinPts为7，则点$p_1$,$p_2$和$p_3$为核心对象；点$p_4$为非核心对象；
点$p_1$直接密度可达点$p_2$、点$p_3$直接密度可达点$p_4$、点$p_1$直接密度可达点$p_4$，所以点$p_4$密度可达点$p_3$；点$p_4$为核心点$p_3$的边界点。

如上图所示，如果$ϵ$为3，MinPts为7，则点o，$p_1$和$q_1$为核心对象；点$p_2$和$q_2$为非核心对象；
由于点o密度可达点$p_2$，并且点o密度可达点$q_2$，则称点$P_2$和点$q_2$是密度相连的，如果点$P_2$和点$q_2$是最大的密度相连，则上图中的所有样本点构成一个簇；由于点N不属于上图中呈现的簇，故将其判断为异常点。

密度聚类的具体步骤：

步骤讲解
1.为密度聚类算法设置一个合理的半径$ϵ$以及$ϵ$领域内包含的最少样本量Minpts。
2.从数据集中随机挑选一个样本点p,检验其在$ϵ$领域内是否包含指定的最少样本量，如果包含就将其定性为核心对象，并构成一个簇C；否则，重新挑选一个样本点。
3.对于核心对象p所覆盖的其他样本点q,如果点q对应的$ϵ$领域内仍然包含最少样本量MinPts,就将其覆盖的样本点统统归于簇C.
4.重复步骤3，将最大的密度相连所包含的样本点聚合为一类，形成一个大簇。
5.完成步骤4后，重新回到步骤2，并重复步骤3和步骤4，直到没有新的样本点可以生成新簇时算法结束。