AVL树插入接口涉及到的四个旋转

AVL树插入接口:涉及到4个旋转。

从接口出发:

主要分为以下几个步骤:

1.找到插入的位置

2.将需要插入的点插入进树

3.更新平衡因子(如果不平衡,则进入第4步) 

4.旋转调节平衡因子  (重点)

bool AVLTree<T>::Insert(const T& data)
{
	if (_pRoot == nullptr) 若AVL树为空树，则插入结点直接作为根结点
	{
		_pRoot = new Node(data);
		return true;
	}
	1、按照二叉搜索树的插入方法，找到待插入位置
	Node* cur = _pRoot;
	Node* parent = nullptr;
	while (cur)
	{
		if ( data < cur->_data) 待插入结点的key值小于当前结点的key值
		{
			//往该结点的左子树走
			parent = cur;
			cur = cur->_pLeft;
		}
		else if (data > cur->_data) 待插入结点的key值大于当前结点的key值
		{
			往该结点的右子树走
			parent = cur;
			cur = cur->_pRight;
		}
		else 待插入结点的key值等于当前结点的key值
		{
			插入失败（不允许key值冗余）
			return false;
		}
	}

	2、将待插入结点插入到树中
	cur = new Node(data); 根据所给值构造一个新结点
	if (data < parent->_data) 新结点的key值小于parent的key值
	{
		插入到parent的左边
		parent->_pLeft = cur;
		cur->_pParent = parent;
	}
	else 新结点的key值大于parent的key值
	{
		插入到parent的右边
		parent->_pRight = cur;
		cur->_pParent = parent;
	}

	3、更新平衡因子，如果出现不平衡，则需要进行旋转
	while (cur != _pRoot) 最坏一路更新到根结点
	{
		if (cur == parent->_pLeft) parent的左子树增高
		{
			parent->_bf--; parent的平衡因子--
		}
		else if (cur == parent->_pRight) parent的右子树增高
		{
			parent->_bf++; parent的平衡因子++
		}

		判断是否更新结束或需要进行旋转
		if (parent->_bf == 0) 更新结束（新增结点把parent左右子树矮的那一边增高了，此时左右高度一致）
		{
			break; parent树的高度没有发生变化，不会影响其父结点及以上结点的平衡因子
		}
		else if (parent->_bf == -1 || parent->_bf == 1) 需要继续往上更新平衡因子
		{
			parent树的高度变化，会影响其父结点的平衡因子，需要继续往上更新平衡因子
			cur = parent;
			parent = parent->_pParent;
		}
		else if (parent->_bf == -2 || parent->_bf == 2) 需要进行旋转（此时parent树已经不平衡了）
		{
			if (parent->_bf == -2)
			{
				if (cur->_bf == -1)
				{
					RotateR(parent); 右单旋
				}
				else    cur->_bf == 1
				{
					RotateLR(parent); 左右双旋
				}
			}
			else        parent->_bf == 2
			{
				if (cur->_bf == -1)
				{
					RotateRL(parent); 右左双旋
				}
				else cur->_bf == 1
				{
					RotateL(parent); //左单旋
				}
			}
			break; 旋转后就一定平衡了，无需继续往上更新平衡因子(旋转后树高度变为插入之前了)
		}
		else
		{
			assert(false); 在插入前树的平衡因子就有问题
		}
	}
	return true; 插入成功
}

旋转第一招:左单旋

1.了解什么时候需要左单旋！

 

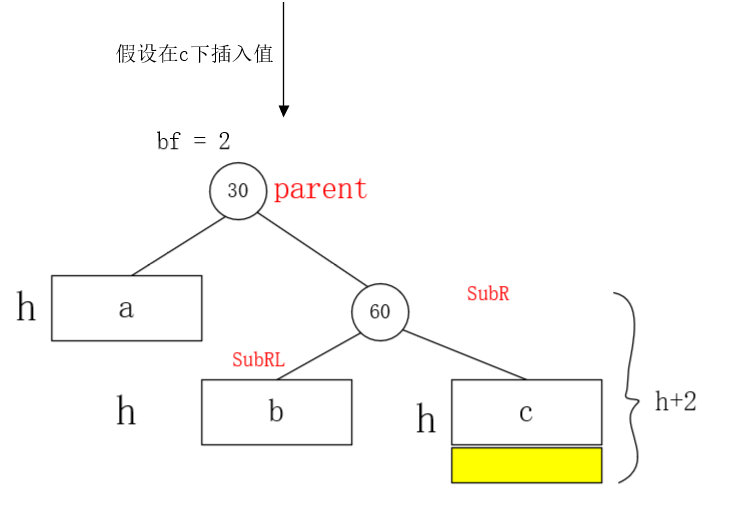
 此时需要我们进行左单旋。

 左单旋后的结果：

此时还需要再更新平衡因子。

可以看出,此时SubR与parent的平衡因子均为0。

代码实现:

template<class T>
struct AVLTreeNode
{
	AVLTreeNode(const T& data = T())
		: _pLeft(nullptr)
		, _pRight(nullptr)
		, _pParent(nullptr)
		, _data(data)
		, _bf(0)
	{}

	AVLTreeNode<T>* _pLeft;
	AVLTreeNode<T>* _pRight;
	AVLTreeNode<T>* _pParent;
	T _data;
	int _bf;   // 节点的平衡因子
};

template<class T>
void AVLTree<T>::RotateL(Node* pParent)
{
	Node* SubR = pParent->_pRight;
	Node* SubRL = SubR->_pLeft;
	Node* parentParent = pParent->_pParent;

	//建立SubRL与pParent的关系
	pParent->_pRight = SubRL;
	if (SubRL)
	{
		SubRL->_pParent = pParent;
	}
	//建立parent与SubR的关系
	SubR->_pLeft = pParent;
	pParent->_pParent = SubR;
	
	//建立SubR与parentParent的关系 
    //parentParent如果为空,证明parent是根节点。
	if (parentParent ==nullptr)
	{
		_pRoot = SubR;
		_pRoot->_pParent = nullptr;
	}
	else
	{
		if (pParent == parentParent->_pLeft)
		{
			parentParent->_pLeft = SubR;
		}
		else
		{
			parentParent->_pRight = SubR;
		}
		SubR->_pParent = parentParent;
	}
	SubR->_bf = 0;
	pParent->_bf = 0;
}

旋转第二招:右单旋

与左单旋类型类似,

右单旋前：

 

右单旋后:

 此时SubL的平衡因子为0,parent的平衡因子为0。

代码实现:

template<class T>
void AVLTree<T>::RotateR(Node* pParent)
{
	Node* SubL = pParent->_pLeft;
	Node* SubLR = SubL->_pRight;
	Node* parentParent = pParent->_pParent;

	//建立parent和SubL的关系
	SubL->_pLeft = pParent;
	pParent->_pParent = SubL;

	//建立parent和SubLR的关系
	if (SubLR)
	{
		pParent->_pRight = SubLR;
		SubLR->_pParent = pParent;
	}

	//建立SubL与parentParent之间的关系
	if (parentParent == nullptr)
	{
		_pRoot = SubL;
		_pRoot->_pParent = nullptr;
	}
	else
	{
		if (pParent == parentParent->_pLeft)
		{
			parentParent->_pLeft = SubL;
		}
		else
		{
			parentParent->_pRight = SubL;
		}
		SubL->_pParent = parentParent;
	}
	pParent->_bf = 0;
	SubL->_bf = 0;
}

旋转第三招:左右旋

如图这样的情况:插入值后,其高度改变为h,至两边高度差为2.

插入的值在a,b,c 均会影响平衡,本文仅讨论在b进行插入值的情况。

左旋前:

 对SubL进行左旋。

左旋后：

 

 此时:两边依旧不平衡。如果我们将图进行简化:

 再进行右旋: 对parent进行右旋

 最后，进行平衡因子的修改

平衡因子的情况分为三种:

1、当subLR原始平衡因子是-1时，左右双旋后parent、subL、subLR的平衡因子分别更新为1、0、0。

2、当subLR原始平衡因子是1时，左右双旋后parent、subL、subLR的平衡因子分别更新为0、-1、0。

3、当subLR原始平衡因子是0时，左右双旋后parent、subL、subLR的平衡因子分别更新为0、0、0。

三种情况读者有兴趣可以自己验证一下。

总结:

左右双旋:1.对SubL进行左旋  2.对parent 进行右旋

代码实现:

template<class T>
void AVLTree<T>::RotateLR(Node* pParent)
{
	Node* SubL = pParent->_pLeft;
	Node* SubLR = SubL->_pRight;
	//先对SubL进行左单旋
	RotateL(SubL);
	//再对pParent进行右单旋
	RotateR(pParent);

	//最后更新平衡因子。
	if (SubL->_bf == -1)
	{
		pParent->_bf = 1;
		SubL->_bf = 0;
		SubLR->_bf = 0;
	}
	else if (SubL->_bf == 1)
	{
		pParent->_bf = 0;
		SubL->_bf = -1;
		SubLR->_bf = 0;
	}
	else if (SubLR->_bf == 0)
	{
		pParent->_bf = 0;
		SubL->_bf = 0;
		SubLR->_bf = 0;
	}
	else
		assert(false);
}

 旋转第四招:右左旋

在b、c、d下插入均会影响平衡,本文仅讨论在b下插入值的情况。

 此时,对SubR进行右单旋:

再对parent进行左单旋:

 

 此时再进行平衡因子的修改:

右左双旋后，平衡因子的更新随着subLR原始平衡因子的不同分为以下三种情况：
1、当subRL原始平衡因子是1时，左右双旋后parent、subR、subRL的平衡因子分别更新为-1、0、0。

2、当subRL原始平衡因子是-1时，左右双旋后parent、subR、subRL的平衡因子分别更新为0、1、0。

3、当subRL原始平衡因子是0时，左右双旋后parent、subR、subRL的平衡因子分别更新为0、0、0。

代码实现:

template<class T>
void AVLTree<T>::RotateRL(Node* pParent)
{
	Node* SubR = pParent->_pRight;
	Node* SubRL = SubR->_pLeft;
	RotateR(SubR);
	RotateL(pParent);
	if (SubRL->_bf == 1)
	{
		pParent->_bf = -1;
		SubR->_bf = 0;
		SubRL->_bf = 0;
	}
	else if (SubRL->_bf == -1)
	{
		pParent->_bf = 0;
		SubR->_bf = 1;
		SubRL->_bf = 0;
	}
	else if (SubRL->_bf == 0)
	{
		pParent->_bf = 0;
		SubR->_bf = 0;
		SubRL->_bf = 0;
	}
	else
		assert(false);
}

总结:

右左双旋:1.对SubR进行右旋  2.对parent 进行左旋