第 45 届国际大学生程序设计竞赛（ICPC）亚洲区域赛（济南）(热身赛) C-GPA

题目

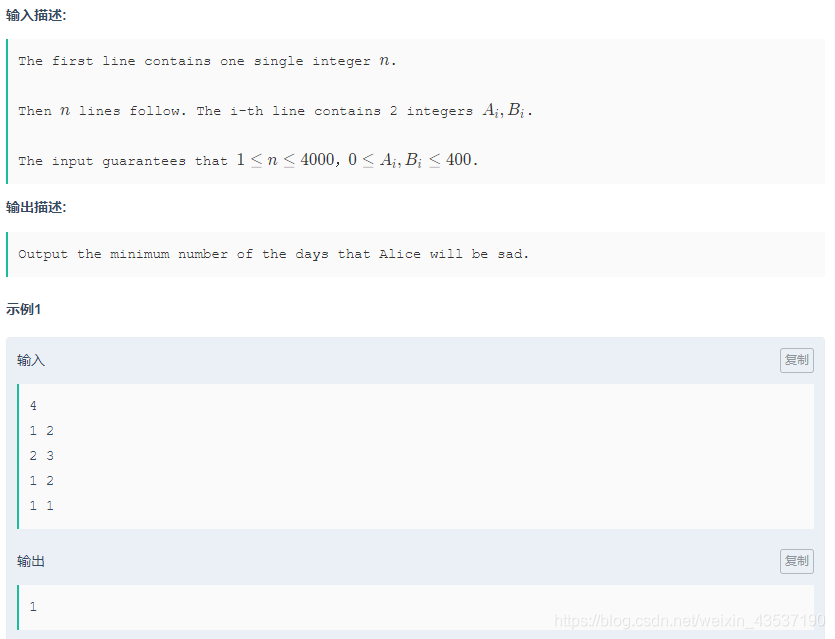
In this term, Alice took nn courses. Now, she has finished all final exams, and she will get her grades in the following nn days.

On the i-th day, Alice will know her grade of the i-th course, denoted as $A_i$is strictly less than the average grade of the first $i-1$ courses, Alice will be sad on that day.

Now Bob hacks into the school’s database. Bob can choose a set S of courses (S can be empty), and then for each course ii in S, change Alice’s grade from $A_i$ to $B_i$Bob wants to minimize the number of days that Alice will be sad. Now you need to help him to decide which courses’ grades he should modify.

Note: Alice is always happy on the first day.

题意

给定长度为n的a数组和b数组，分别是Alice获得的成绩和Bob可以换的成绩，如果当前这天的成绩严格小于前i-1天的平均成绩，则Alice会伤心。Bob可以把b数组的值换到a数组中，问Alice最少可以伤心多少天。

思路

考虑dp，计算出前i天有j天伤心需要的最小分数，如果当前选a可以让Alice不伤心的话就更新dp[i][j]最小值(前i天伤心的天数没有增加)，否则更新dp[i][j+1]的最小值(前i天伤心的天数增加1) ，最后从1-n如果有可实现的方案直接输出即可。
注意 由于：
sum[i-1]/i-1 < a[i]
所以可以变形为：
sum[i-1]<(i-1)*a[i]
详情见代码

代码

#include <bits/stdc++.h>
using namespace std;

const int maxn = 4000+100;

int a[maxn],b[maxn];
int dp[maxn][maxn]; // 前i天有j天伤心的最小成绩和 
int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i] >> b[i];
	memset(dp,0x3f,sizeof dp);
	
	dp[1][0] = min(a[1],b[1]); // 前1天有0天伤心的最小需要的成绩 
	for(int i=2;i<=n;i++)
	{
		for(int j=0;j<i;j++)
		{
			if(dp[i-1][j] <= (i-1) * a[i])//如果今天选择a可以不伤心 
			dp[i][j] = min(dp[i][j],dp[i-1][j] + a[i]); // 就不加伤心的天数，并且更新答案
			else // 如果今天选择a不能不伤心
			dp[i][j+1] = min(dp[i][j+1],dp[i-1][j] + a[i]); //就加一天伤心天数，并且更新答案 
			
			if(dp[i-1][j] <= (i-1) * b[i]) // 和a同理 
			dp[i][j] = min(dp[i][j],dp[i-1][j] + b[i]);
			else 
			dp[i][j+1] = min(dp[i][j+1],dp[i-1][j] + b[i]);
		}
	}
	
	for(int i=1;i<=n;i++)
	{
		if(dp[n][i] != 0x3f3f3f3f) return cout<<i,0;
	}
	cout<<n;
	return 0;
}
/*
sum[i-1]/i-1 <= a[i] 
变形： 
sum[i-1] <= (i-1)*a[i]
*/