网格矩阵左上角到右下角的最短路径

题目描述

绘图工具：
processon
​xiaohuazhuo

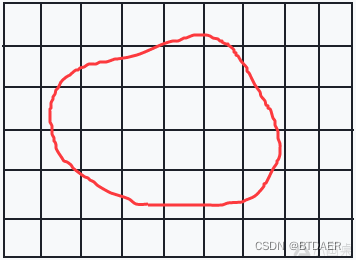
如下图，从网格左上角走到右下角，红色区域内为障碍物无法通行，要求找到最短路径
​​​​​​​​​​​​​​

参考

[编程题]求最短通路值

用一个整形矩阵matrix表示一个网格，1代表有路，0代表无路，每一个位置只要不越界，都有上下左右四个方向，求从最左上角到右下角的最短通路值

例如，matrix为：

1 0 1 1 1

1 0 1 0 1

1 1 1 0 1

0 0 0 0 1

通路只有一条，由12个1构成，所以返回12

[要求]
时间复杂度为 $O(nm)$ ，空间复杂度为 $O(nm)$

输入描述:
第一行两个整数N，M表示矩形的长宽
接下来N行，每行一个长度为M的字符串表示矩形

输出描述:
输出一个整数表示最小步数
若从(1, 1)无法到达(n, m)请输出-1