斐波拉切数列--实例

最新推荐文章于 2020-02-26 15:15:44 发布

原创

最新推荐文章于 2020-02-26 15:15:44 发布 · 1.1k 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#斐波那契数列-举例

这篇博客探讨了如何运用斐波那契数列来解决两种问题：一是用n个2 * 1的小矩形无重叠覆盖2 * n的大矩形的方法计数，二是计算一只青蛙跳上n级台阶的不同跳法。对于矩形覆盖问题，博主提供了排列组合和斐波那契数列两种解题思路；而对于跳台阶问题，直接应用斐波那契数列即可。每种方法都附带了解题思路和代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、矩形覆盖：
1.题目描述：
我们可以用2 * 1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2 * 1的小矩形无重叠地覆盖一个2 * n的大矩形，总共有多少种方法？
在这里插入图片描述
2.解题思路：
解法一：排列组合，假设竖方块的数量是y，横方块的数量是x，可知x+2*y=target,用for循环遍历x，并用递归的方法对数量为x的横方块和数量为y的竖方块进行排列组合。（比较复杂）

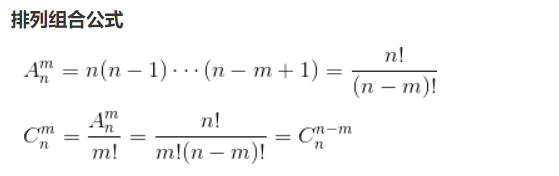
排列的定义：从n个不同元素中，任取m(m≤n,m与n均为自然数,下同）个元素按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列；
组合的定义：从n个不同元素中，任取m(m≤n）个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合；

解法二：斐波那契数列，经过举例发现该问题符合菲波那切数列的特点。

3.代码：
解法一：

public class Solution {
    public int RectCover(int target) {
        int x;
        int y;
        int count = 0;
        if(target == 0){
            return 0;
        }
        for(x = 0; x <= target; x++){
            y = (target - x)/