动态规划概述:
-
动态规划是一种通过子问题的解来求原问题解的递归算法。动态规划是用来求解重叠子问题的,即不同的问题具有公共子问题。
-
动态规划的核心就是对每个子问题只求解一次,将每个子问题的结果保留在一个数组中,从而无需每次求解子问题时都要重复计算,避免了不必要的重复计算。
动态规划方法求解的问题类型:
(1)**最优化问题:**对于一个问题有许多可行解,每一个解都有一个值,要求寻找具有最优值的解。如:背包问题、最长上升子序列等问题等。
(2)组合计数问题: 对于一个解组合问题有多种选法,计算选取方法有多少种。例如:组合计数问题、数位统计问题、基于连通性的动态规划等。
(3)**可行性问题:**对于一个问题判断是否具有可行解。例如,动态规划求解博弈类问题。
1.数字三角形
问题描述:
一个数字三角形宝塔,数字三角形中的数字都是不超过100的正整数。现在规定一个人从最顶层走到最底层,每一步可沿左斜线或右斜线向下走。求解从顶层到最底层的一条路径,使得沿着该路径所经过的数字的总和最大,输出最大值。

一般问题分析: 我们可以通过搜索所有的路径和每条路径对应的数字之和,从中找出最大值。这种搜索算法的时间复杂度为O(路径条数),每个节点的出度为2,所以路径条数为2^n。其中n为数字三角形的高度。
动态规划思想:(1)定义f(x,y):表示从第x行第y列出发到达最底层路径所经过的数字的总和最大值:
(2)推导f(x,y)递推式:
f(x,y)=0 (x>n)
f(x,y)=max ( f(x+1,y), f(x+1,y+1) + a(x,y) ) (x不等于n)
式中a(x,y)为数字三角形中第x行第y列的数字。
动态规划方法计算数字三角形的代码如下(c++):
int F(int x, int y, int f[1010][1010],a[1010][1010])//当人在(x,y)处
{ if(f[x][y] != -1)return f[x][y];//如果这个状态已经搜索过那么直接返回答案
if(x>n)return 0;
return f[x][y] = max(F(x+1,y+1),F(x+1,y))+a[x][y];
}
2.组合数
从n个不同元素中取出m个元素的所有组合的个数,叫做组合数问题。
组合数的公式为(1):

如果从n个物品中选取m个物品,则存在(2)式。下面证明:
从n个数中选取m个不同数的方法为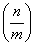
对于数字n来说,当n被选中时方法数为: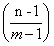
同理当n没有被选中时,方法数为: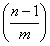
下面通过动态规划方法运用以上公式计算组合数:
constint mod=1e9+7;
int DFS(int n, int m, int C[1010][1010]){
if(n<m)return 0;
if(n == m||m == 0)return 1;
int&ret=C[n][m];
if(ret+1)return ret;
ret=DFS(n-1,m-1)+DFS(n-1,m);
ret%=mod;
return ret;
}
3. 背包问题之0-1背包
问题描述:
现在有N件物品和一个容量为V的背包。第i件物品占用Ci的空间,价值是Wi。求解将哪些物品装入背包,可以在满足背包空间条件下让背包内物品价值总和最大。这是最基础的背包问题,特点是:每种物品仅有一件,可以选择放或者不放。
可以采用如下动态规划方法求解:
(1)定义f(x,y):表示前x个物品放入一个容量恰为y的背包可以获得的最大价值
(2)推导f(x,y)递推式:
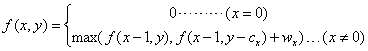
以上方法的时间和空间复杂度为O(VN),其中时间复杂度应该已经不能再优化了,但空间复杂度可以优化到O(V)。
for (int i=1;i<=N; i++)
for(int j=v[i]; j<=V; j++)
f[i][j] = max(f[i-1][j], f[i-1][j-c[i]] + w[i]);
我们可以用滚动数组法来优化空间,因为前i个物品的最优值只与前i-1个物品的最优值有关,所以只需要两个长度为v的数组,用f[0]来表示f[i-1]数组的值,f[1]表示f[i]数组的值。滚动数组法优化0-1背包的代码如下:
for (int i=1;i<=N;i++)
{
for(int j =v[i];j<=V;j++)
f[1][j]=max( f[0][j], f[0][ j-c[i]] + w[i]);
for (int j=1; j<=V; j++)
f[0][j] = f[1][j];
}
滚动数组法使用了两个O(V)的数组,将O(NV)的空间复杂度降低到O(V),但是依然可以继续优化。优化思路就是如何去掉f[1]这个数组,设法用f[0]数组来完成对自身的更新。
4.背包问题之完全背包
问题描述:
有N件物品和一个容量为V的背包,第i中物品中的一件占用ci的空间,价值是wi,每种物品都有无限多个。求解将哪些物品装入背包可以使得价值总和最大。
我们可以看出,完全背包和0-1背包的区别在于:每一种物品0-1背包最多可以放一个,而完全背包却能放任意多个。我们对一类物品拆解,如果一个物品占用空间为c[i],那么最多能放下【V/c[i]】个物品。就可以把某一类物品拆成【V/c[i]】个物品,这样第i类物品有k个占用k×c[i]的空间,价值为k×v[i],这样,完全背包就转化为0-1背包问题。
(1):定义f(x,y):表示前x个物品恰好放入一个容量为y的背包可以获得的最大价值。
(2)推导f(x,y)递推式:
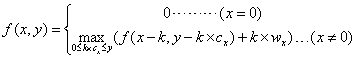
5.背包问题之多重背包
问题描述:
有N种物品和一个容量为V的背包,第i中物品最多有mi个,每件耗费的空间li的价值是wi。求解将哪些物品装入背包可使得这些物品的消耗的空间总和不超过背包容量,且价值总和最大。
对于第i种物品有mi+1种策略:取0件,取1件,、、、、、、,取mi件。
按照动态规划方法的解题思路:
(1)定义f(x,y):表示前x件物品恰好放入一个容量为y的背包可以获得的最大价值。
(2)推导f(x,y)递推式:
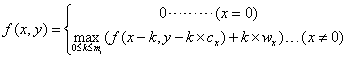
优化的关键在于减少分解出的物品,朴素的方法直接把一类物品分成了m[i]个物品,那么我们讲解一下如何减少分解出的物品:
关键是数字的二进制表示,如果有1,2,4,········,2^k这k个数字,那么就能表示1到2的(k-1)次方的所有数字。由于拆分的都是2的幂,那么一类物品最多拆分为log2 N个物品。
6.最长上升子序列
问题描述:
给出一个由n个数组组成的序列x[1```````n],找出它的最长单调上升子序列。即求最大的m及一个依次递增的序列a1, a2, ·······、am,并且序列对应的x值也依次递增,x[a1]<x[a2]<·······<x[am]。
按照动态规划方法的解题思路:
(1)定义f(x): 表示以第x个数结尾的最长上升子序列的长度。
(2)推导f(x)递推式:
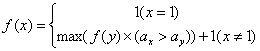





 本文介绍了动态规划的基本概念和应用,包括数字三角形的最大路径和组合数计算。接着详细探讨了不同类型的背包问题,如0-1背包、完全背包和多重背包的动态规划解决方案。最后,讨论了如何使用动态规划解决最长上升子序列问题。文章通过递推公式和代码示例阐述了动态规划的思想和应用。
本文介绍了动态规划的基本概念和应用,包括数字三角形的最大路径和组合数计算。接着详细探讨了不同类型的背包问题,如0-1背包、完全背包和多重背包的动态规划解决方案。最后,讨论了如何使用动态规划解决最长上升子序列问题。文章通过递推公式和代码示例阐述了动态规划的思想和应用。
















 5700
5700

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








