图解红黑树

写在前面

阅读本文你需具备知识点：

• 二叉树
• 平衡二叉树AVL

红黑树也是一棵二叉查找树，既然有了AVL树为什么还需要红黑树呢？

之前在了平衡二叉树AVL实现中讲到了为什么使用平衡二叉树AVL（解决二叉查找树退化为类似链表的问题），最大的作用就是用于查找，其时间复杂度为O(logn)，但AVL树插入或删除节点后，若使得高度之差大于1，此时，AVL树的平衡状态就被破坏，需要旋转才能达到平衡。因此如果在插入和删除频繁的场景中就需要频繁的调整使之达到平衡，性能也随之下降。

因此，红黑树的提出是为了解决平衡树在插入和删除等操作频繁的情况。

在了解红黑之前先看看2-3-4树。

2-3-4树

在二叉树中，每个节点有一个数据项（可以理解为节点的值，key），最多有2个子节点。如果允许每个节点可以有更多的数据项和子节点，就是多叉树，2-3-4树就属于多叉树，并且还是平衡树（B树）。

2-3-4树是一种阶（阶，可以理解为节点的分支）为4的B树，所以也可称它为4叉树，主要具备以下性质：

1. 有1个key的节点有2个子节点，有2个key的有3个子节点，有3个key的有4个子节点，对应key的节点分别称为2节点，3节点，4节点，这也是为什么叫2-3-4树的原因

2. 所有的叶子节点总在同一层

3. 每个节点的值从左到右保持了从小到大的顺序，两个key之间的子树中所有的key一定大于它的父节点的左key，小于父节点的右key。如下

   

如下面这棵2-3-4树：

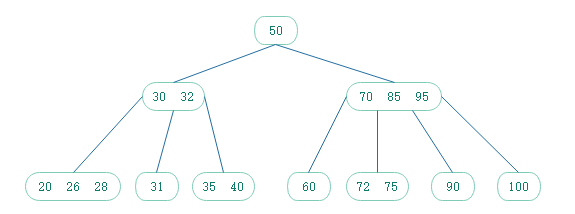
在上图中：

有2个链接的为2节点

有3个链接的为3节点

有4个链接的为4节点

插入操作

2-3-4树的插入总是在叶子节点且一般不允许插入重复的key。

若插入时的叶子节点不是满节点（即4节点），如插入数据45，如下：

节点分裂

如果插入节点是4节点，这时候节点就需要分裂才能保证树的平衡（这里假设分裂的节点不是根节点），一个4节点可以分裂成一个根节点和两个子节点（这三个节点各含一个key）然后在子节点中插入。若分裂的节点数据分别用ABC来表示：

若分裂节点的父节点也是满节点，则按照分裂操作继续分裂即可。

2-3-4树的删除如果感兴趣的可自己去百度，网上很多

点这

红黑树

红黑树也是一棵二叉查找树，也是一棵自平衡树，具备以下性质：

1. 节点是红色或黑色（非黑即红）
2. 根节点是黑色
3. 所有的null节点称为叶子节点，且都是黑色
4. 所有红色节点的子节点都是黑色（即没有连续的红色节点）
5. 任意一个节点到其叶子节点的所有路劲都包含相同数目的黑色节点

如下面这个常见的红黑树：

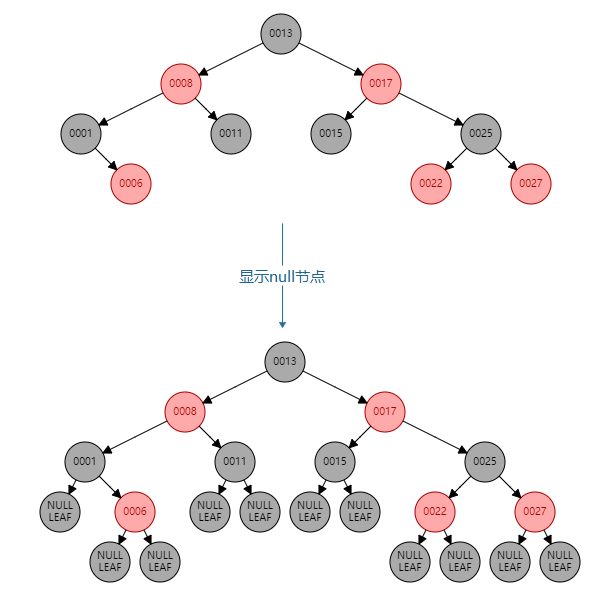
通过以上性质，可以推出：从根节点到叶子节点的最长路径不会超过最短路径的2倍

为什么？

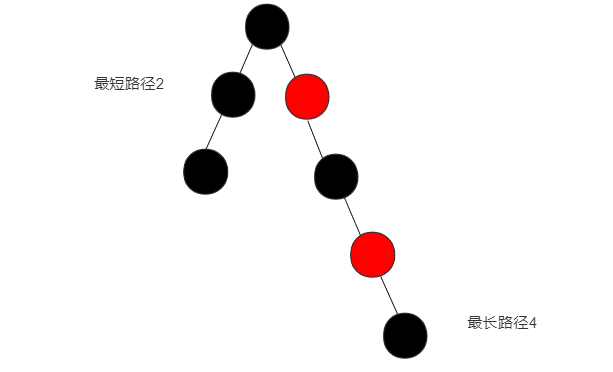
根据上面的性质5我们知道下图的红黑树每条路径上都是3个黑结点。因此最短路径长度为2(没有红结点的路径)。再根据性质4(没有连续的红色节点)和性质2，3(叶

子和根必须是黑结点)。那么我们可以得出：

最短路径：一条具有3个黑结点的路径上最多只能有2个红结点(红黑间隔存在)，最短路径为2。

最长路径：黑深度为2（根结点也是黑色）的红黑树最长路径为4。

从这一点我们可以看出红黑树是大致平衡的。 (比平衡二叉树要差一些，AVL的平衡因子最多为1)

注：若以下有说道性质1-5，分别表示上述性质，如性质2表示“根节点是黑色”。

2-3-4树和红黑树的等价关系

红黑树起源于2-3-4树，一颗红黑树对应一颗确定的2-3-4树，一颗2-3-4树对应多个红黑树。

上面的2-3-4树和红黑树看上去完全不同，但实际上是等价的，通过一些规则可以让2-3-4树变为红黑树，如：