函数 $f(z) = |z|^2$ 的性质

引言

复变函数是指定义在复数域上的函数，其自变量和因变量都是复数。复变函数的导数定义与实变函数类似，但有其独特之处。对于一个复变函数 $f(z)$ 在点 $z_0$ 可导，意味着极限

$$f^{\prime }(z_0)=\underset{\Delta z\to 0}{\lim }\frac{f(z_0+\Delta z)-f(z_0)}{\Delta z}$$

存在且与 $\Delta z$ 趋近于 0 的方式无关。这一要求比实变函数的可导性更为严格，也引出了复变函数解析性的概念。

函数 $f(z)=|z{|}^2$ 的定义

首先，明确 $f(z)=|z{|}^2$ 的具体表达式。设 $z=x+iy$，其中 $x,y\in \mathbb{R}$，则 $|z|=\sqrt{x^2+y^2}$，因此

$$f(z)=|z{|}^2=x^2+y^2$$

所以，可以将 $f(z)$ 表示为：

$$f(z)=f(x+iy)=x^2+y^2$$

函数 $f(z)=|z{|}^2$ 的映射性质

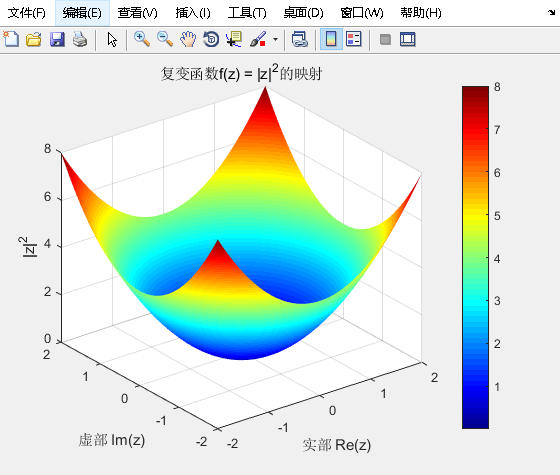
1. 实值函数：$f(z)=|z{|}^2$将复数映射到实数，因此其图像是三维空间中的曲面。

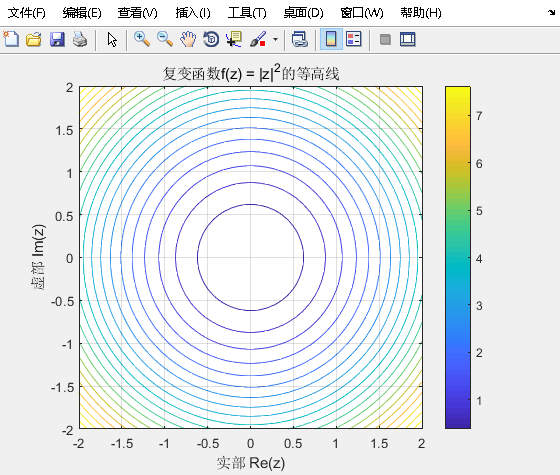
2. 旋转对称性：函数值仅取决于模$|z|$，因此在复平面上具有旋转对称性。等高线图显示为同心圆。

3. 抛物面：在三维视图中，函数图像是一个旋转抛物面，因为$f(z)=x^2+y^2$。

Matlab演示

% 定义网格范围
[x, y] = meshgrid(linspace(-2, 2, 50), linspace(-2, 2, 50));
z = x + 1i*y;  % 创建复数网格

% 计算函数值
f = abs(z).^2;  % 等价于 x.^2 + y.^2

% 绘制三维曲面
figure;
surf(x, y, f);
title('复变函数f(z) = |z|^2的映射');
xlabel('实部 Re(z)');
ylabel('虚部 Im(z)');
zlabel('|z|^2');
colormap('jet');
colorbar;
shading interp;

% 绘制等高线图
figure;
contour(x, y, f, 20);
title('复变函数f(z) = |z|^2的等高线');
xlabel('实部 Re(z)');
ylabel('虚部 Im(z)');
colorbar;
grid on;
axis equal;

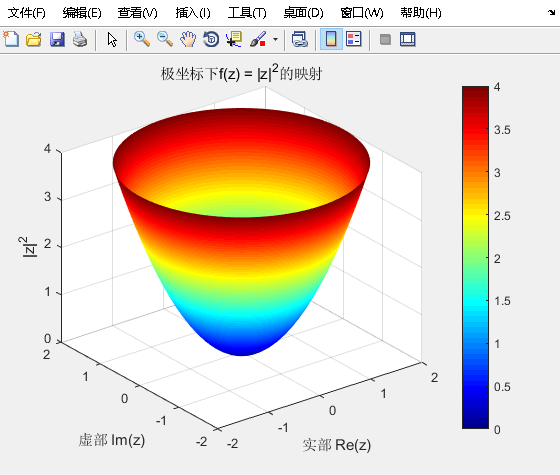
% 绘制极坐标下的映射
theta = linspace(0, 2*pi, 100);
r = linspace(0, 2, 20);
[Theta, R] = meshgrid(theta, r);
Z = R .* exp(1i*Theta);
F = abs(Z).^2;

figure;
surf(R.*cos(Theta), R.*sin(Theta), F);
title('极坐标下f(z) = |z|^2的映射');
xlabel('实部 Re(z)');
ylabel('虚部 Im(z)');
zlabel('|z|^2');
colormap('jet');
colorbar;
shading interp;

运行结果：

复变函数可导的必要条件：柯西-黎曼方程

复变函数 $f(z)=u(x,y)+iv(x,y)$ 在某点可导的必要条件是满足柯西-黎曼方程：

$$\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y},\frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x}$$

对于 $f(z)=x^2+y^2$，可以将其表示为：

$$u(x,y)=x^2+y^2,v(x,y)=0$$

计算偏导数：

$$\frac{\partial u}{\partial x}=2x,\frac{\partial u}{\partial y}=2y$$
$$\frac{\partial v}{\partial x}=0,\frac{\partial v}{\partial y}=0$$

代入柯西-黎曼方程：

1. $\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y}$ ⇒ $2x=0$
2. $\frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x}$ ⇒ $2y=-0$ ⇒ $2y=0$

因此，只有在 $x=0$ 且 $y=0$ 时，即 $z=0$ 点，柯西-黎曼方程才成立。这意味着 $f(z)=|z{|}^2$ 仅在 $z=0$ 处可能可导。

验证 $z=0$ 处的可导性

现在验证 $f(z)$ 在 $z=0$ 处是否可导。根据导数的定义：

$$f^{\prime }(0)=\underset{\Delta z\to 0}{\lim }\frac{f(0+\Delta z)-f(0)}{\Delta z}=\underset{\Delta z\to 0}{\lim }\frac{|\Delta z{|}^2-0}{\Delta z}=\underset{\Delta z\to 0}{\lim }\frac{|\Delta z{|}^2}{\Delta z}$$

设 $\Delta z=\Delta x+i\Delta y$，则 $|\Delta z{|}^2=\Delta x^2+\Delta y^2$，所以：

$$f^{\prime }(0)=\underset{(\Delta x,\Delta y)\to (0,0)}{\lim }\frac{\Delta x^2+\Delta y^2}{\Delta x+i\Delta y}$$

考虑 $\Delta z$ 沿不同路径趋近于 0：

1. 沿实轴（$\Delta y=0$）：

$$f^{\prime }(0)=\underset{\Delta x\to 0}{\lim }\frac{\Delta x^2}{\Delta x}=\underset{\Delta x\to 0}{\lim }\Delta x=0$$

2. 沿虚轴（$\Delta x=0$）：

$$f^{\prime }(0)=\underset{\Delta y\to 0}{\lim }\frac{\Delta y^2}{i\Delta y}=\underset{\Delta y\to 0}{\lim }\frac{\Delta y}{i}=0$$

3. 沿 $\Delta y=k\Delta x$（$k$ 为常数）：

$$f^{\prime }(0)=\underset{\Delta x\to 0}{\lim }\frac{\Delta x^2+k^2\Delta x^2}{\Delta x+ik\Delta x}=\underset{\Delta x\to 0}{\lim }\frac{(1+k^2)\Delta x^2}{(1+ik)\Delta x}=\underset{\Delta x\to 0}{\lim }\frac{(1+k^2)\Delta x}{1+ik}=0$$

无论 $\Delta z$ 以何种方式趋近于 0，极限都为 0。因此，$f(z)$ 在 $z=0$ 处可导，且导数为 0。

其他点的不可导性

对于 $z\ne 0$，我们已经通过柯西-黎曼方程得出 $f(z)$ 不满足可导的必要条件。为了更直观地理解这一点，可以尝试直接计算导数。

设 $z_0\ne 0$，计算导数：

$$f^{\prime }(z_0)=\underset{\Delta z\to 0}{\lim }\frac{f(z_0+\Delta z)-f(z_0)}{\Delta z}=\underset{\Delta z\to 0}{\lim }\frac{|z_0+\Delta z{|}^2-|z_0{|}^2}{\Delta z}$$

展开 $|z_0+\Delta z{|}^2$：

$$|z_0+\Delta z{|}^2=(z_0+\Delta z)(\overline{z_0}+\overline{\Delta z})=z_0\overline{z_0}+z_0\overline{\Delta z}+\overline{z_0}\Delta z+\Delta z\overline{\Delta z}=|z_0{|}^2+z_0\overline{\Delta z}+\overline{z_0}\Delta z+|\Delta z{|}^2$$

因此：

$$\frac{|z_0+\Delta z{|}^2-|z_0{|}^2}{\Delta z}=\frac{z_0\overline{\Delta z}+\overline{z_0}\Delta z+|\Delta z{|}^2}{\Delta z}=z_0\frac{\overline{\Delta z}}{\Delta z}+\overline{z_0}+\frac{|\Delta z{|}^2}{\Delta z}$$

考虑 $\Delta z\to 0$，最后一项 $\frac{|\Delta z{|}^2}{\Delta z}=\overline{\Delta z}\to 0$。因此，主要取决于 $\frac{\overline{\Delta z}}{\Delta z}$ 的行为。

设 $\Delta z=r{e}^{i\theta }$，则 $\overline{\Delta z}=r{e}^{-i\theta }$，所以：

$$\frac{\overline{\Delta z}}{\Delta z}=e^{-2i\theta }$$

当 $\Delta z\to 0$（即 $r\to 0$）时，$\theta$ 可以任意取值，$e^{-2i\theta }$ 依赖于 $\Delta z$ 的趋近方向。因此，除非 $z_0=0$，否则 $\frac{\overline{\Delta z}}{\Delta z}$ 的值依赖于路径，极限不存在。

结论

综上所述：

1. 函数 $f(z)=|z{|}^2$ 仅在 $z=0$ 处可导，且导数为 0。
2. 对于所有 $z\ne 0$，$f(z)$ 不满足柯西-黎曼方程，因此不可导。

进一步讨论

值得注意的是，虽然 $f(z)=|z{|}^2$ 在 $z=0$ 处可导，但它在该点的邻域内并不处处可导。因此，$f(z)$ 在 $z=0$ 处不是解析的（解析要求函数在该点的某个邻域内处处可导）。实际上，$f(z)=|z{|}^2$ 是一个典型的仅在一点可导的函数例子。

此外，$f(z)=|z{|}^2$ 可以表示为 $z\overline{z}$，其中 $\overline{z}$ 是 $z$ 的共轭复数。共轭函数 $\overline{z}$ 本身在任何点都不可导（可以通过柯西-黎曼方程验证），而 $z$ 是全纯的。两个函数的乘积 $z\overline{z}$ 仅在 $z=0$ 处可导，这与实函数中两个可导函数乘积的可导性有所不同。

总结

• 可导点：仅在 $z=0$ 处可导，且 $f^{\prime }(0)=0$。
• 不可导点：对于所有 $z\ne 0$，$f(z)$ 不可导。
• 解析性：$f(z)$ 在 $z=0$ 处不解析，因为解析性要求在某个邻域内可导。

这一例子展示了复变函数可导性与实变函数可导性的显著差异，以及柯西-黎曼方程在判断复变函数可导性中的重要性。