A Bayes Approach to Characterizing Uncertainty in Inverse Problem...........理解

目录：
一、介绍（用的方法）
二、基本方法
  (1)、对粗尺度和细尺度分别介绍
  (2)、例子
  (3)、粗细尺度组合介绍(双尺度)
  (4)、抽样方法的选择
三、例子
  (1)、A SPECT Application （单光子发射断层扫瞄）
  (2)、Application in Hydrology（水文学的应用）
  (3)、Implementation Issues（问题）
四、讨论
  (1)、APPENDIX A
  (2)、APPENDIX B
  (3)、APPENDIX C

一、介绍

  表征不确定性的一种方法是贝叶斯的方法，得到未知参数的后验分布，以概率的形式来表示不确定性。在本文中，我们使用MCMC马尔可夫链蒙特卡罗法来探索未知参数的后验分布(一般来说对于容易采样的分布我们可以直接进行传统的蒙特卡洛采样，但一般我们得到的分布都是不易于采样的)。

  在本文中，我们主要是基于组合马尔可夫链的方法，来探索多尺度(粗、细)的后验，并且使用了一个非常简单的成像问题作为例子来详细的叙述我们这个方法的一个细节。然后，我们有继续考虑两个应用：一个是单光子发射断层扫瞄(SPECT)，一个是在水文学中的应用。

二、基本公式

(1)、对粗尺度和细尺度分别介绍

  (a)、针对于细尺度来说，我们已知观测值$y=(y_1,y_2,......,y_n{)}^T$，对抽样值建模得到似然函数$L(y|x,{\theta }_y)$，未知输入向量$x=(x_1,......x_m)$和$\theta =({\theta }_x,{\theta }_y)$，其中${\theta }_x$是影响先验分布x的参数，${\theta }_y$控制的是似然函数$L(y|x,{\theta }_y)$。假设我们已知了先验分布$\pi (x|{\theta }_x)$和$\pi ({\theta }_x,{\theta }_y)$,我们就可以通过Beyes公式得到参数x和θ的后验分布，并且根据他的后验分布可以通过MCMC法得到参数的平稳分布的采样值。

  (b)、在粗尺度中，我们通过线性变换$\tilde{x}=({\tilde{x}}_1,......,{\tilde{x}}_{\tilde{m}})=Cx$，将输入x的维度降低，在本文中，我们用到的线性变换就是求和或者求平均。因此对于我们的参数和观测值都发生了一定的变化，从原来的$y,\theta$变为了现在的$\tilde{y},\tilde{\theta }$。

  我们由上面的假设可以得到下面的两个尺度下的后验分布：

考虑到在本文中，我们给定x的先验为高斯马尔可夫随机场(MRF)先验，即：

在上式中$W,\tilde{W}$是关于$x,\tilde{x}$的精度矩阵。

(2)、例子(一维图像细尺度建模)

  我们已知有40个观测值$y_i$，图1中显示了我们所观测到的$y_i$值的密度，此外，我们的输入值有40个像素x(维数是40，随机变量个数的取值是40个)，对应了有40组观察值。在这里，我们假设观察值y服从的是泊松分布，所以我们可以得到似然函数$L(y|x)$：

  同样的，x的先验分布，我们假设为高斯分布：

  其中的$\theta ={\theta }_x$控制的是输入x。$m\ast m$维的精度矩阵$W$是三对角线的，主对角线元素$W_{ii}$等于相邻的像素个数，两边副对角线元素$W_{i,i+1}=-1$。最后参数$\theta$的先验为特定的先验：

  所以参数$x,\theta$的后验由贝叶斯公式可以得到：

有了参数的后验分布之后我们就可以通过MCMC法对参数进行更新，MCMC法的过程如下所示：

  以上就是在细尺度下的求解后验参数的过程，而在粗尺度下就是对细尺度中的观测值先进行线性变换，这里用的是相邻两个y值进行求和。将原本的40个观测值降到了20个。具体的参数求解过程和上面相似。

(3)、粗细尺度组合介绍组合

  在纯细尺度下求参数的最优解，当输入向量x的维度很高时，我们就是遇到计算复杂度很高，代价很大等一系列的问题；而我们如果用纯粗尺度求解参数，会遇到求解的参数精度不高等问题，所以在这边作者提出了一个在双尺度下求解参数的方法，这样不仅可以大大的提高了计算速度，也可以在一定程度上提高我们所求得的参数的精度。
  作者提出的一个实现方法时“swapping”更新，将粗细尺度的信息在两者之间移动。就如下图所示：

  在时刻1到2时，我们分别对粗细尺度进行MCMC法对参数进行更新，在时刻2到3时，我们引入提议分布$q$和新的候选值(下一时刻的参数值)$(x^{\ast },{\theta }^{\ast },{\tilde{x}}^{\ast },{\tilde{\theta }}^{\ast })$,其中提议分布的表达式为：

  由此，我们可以得到一个关于参数更新值$(x^{\ast },{\theta }^{\ast },{\tilde{x}}^{\ast },{\tilde{\theta }}^{\ast })$的一个接受率，为下式的最小值：

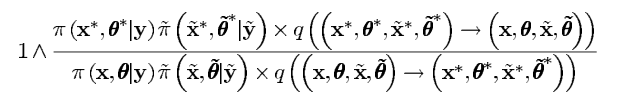
  在这篇文章中，我们把提议分布分解为两项的乘积表示为：

  其中$q((x,\theta )\to ({\tilde{x}}^{\ast },{\tilde{\theta }}^{\ast }))$表示从当前的细尺度状态参数下生成的粗尺度状态参数。反过来同样如此。
  细尺度到粗尺度的过程就是首先通过线性变换$\tilde{x}=Cx$将细尺度的x转换为粗尺度的x(在本文中就是简单的求和或者平均)，然后再根据参数$\theta$关于x的条件分布来求得参数$\theta$的后验概率。所以说$q((x,\theta )\to ({\tilde{x}}^{\ast },{\tilde{\theta }}^{\ast }))$：

  同样的方法作用于$q(((\tilde{x},\tilde{\theta })\to (x^{\ast },{\theta }^{\ast }))$：

  下面我们将之前提出的先验假设带入，看看一维图像中双尺度组合链的实现：


(4)、抽样方法的选择：多尺度组合链
  讲了重要性采样在本文中的应用所遇到的局限性，然后讲在本文中用多尺度组合链的两个优点：首先，耦合链方法很容易适合并行实现，以便每个尺度上的处理量可以很容易地控制。其次，接受概率可以向上文提到的那样可以简化。
三、例子

(1)、A SPECT Application （单光子发射断层扫瞄）
像素化的物体发射的光子强度与物体xi的位置是有关的，伽马相机获得由角度a控制的的不同位置的光子发射的二进制计数bin b(探测到的光子数从0到128)，每个角度和伽马相机的计数bin b 记为数据$y_{ab}$，由于光子可能被散射、吸收等，我们记像素xi发射在角度a和bin b被检测到的概率为$p_{abi}$。
考虑由单光子发射计算机断层扫描生成的数据集$y_{ab}$，目标是由伽马照相机探测到的光子数来重构物体的光子发射强度图。其中对象是一个2维的像素化物体。我们假设角度a的取值为每3°发射光子(共120个角度)。那么假定计数是服从泊松分布的，他的均值是：

用矩阵表示则为：

其中$n=128\ast 120,m=128\ast 128$m是像素xi的数量。
所以在给定对象xi的强度下，可以写出似然函数$L(y|x)$：

以上是在细尺度下的图像重构，而粗尺度在这里我们将像素的数量的范围缩小了四倍，所以：

其中$\tilde{n}=128\ast 120,\tilde{m}=64\ast 64$m是像素xi的数量。所以说，与细尺度计算相比，将像素的数量减少四倍之后，计算也是快了四倍。在之前，我们已经提出了基于粗细尺度的高斯先验，其中精度矩阵是对称矩阵，其对角元素是相邻场址的数量，非对角元素为0或者1(如果场址相邻则为1，否则为0)。
此外，我们最初在第二节的一维成像实例中使用了swap，但是呢我们发现细尺度的提议$x^{\ast }$不够精确。所以在本例中，我们只交换细尺度和粗尺度的内部部分，图5显示了如何去做的。我们交换两幅图像相同的内部区域，粗尺度阴影部分被细化后给出一个好的提议$x^{\ast }$，而细尺度阴影部分被粗化后给出提议${\tilde{x}}^{\ast }$。这样提议被接受的概率会更高一些(大约八分之一的互换提议被接受)。

(2)、Application in Hydrology(双尺度在水文学中的应用)
略
3)、Implementation Issues
  基本思想是使用辅助粗尺度模型预测控制来构造新的候选对象，这些候选对象可以被接受为来自细尺度后验的抽取。显然，对于给定的应用程序，必须权衡利弊。公式越粗糙，向前计算的速度就越快。此外，表述越粗糙，由粗到细的建议被接受的可能性就越低。速度和接受度之间的权衡取决于应用。必须要保持高的接受率。
四、讨论
  以上的研究表明了用粗化的尺度和原尺度相组合，可以大大的减少MCMC法探索后验分布的时间。
(1)、APPENDIX A
讲的是符号注释，上文出现的各个符号代表的含义。
(2)、APPENDIX B
从粗尺度到细尺度的更新：
我们想要从一个单一的多元的分布中画一个细尺度的提议$x^{\ast }$，我们可以从粗尺度下手，从粗尺度$\tilde{x}$中提出提议值$x^{\ast }$，在这里我们要求粗单元格所对应的k个细单元格的平均值必须等于粗单元格。并且设其中的k-1个单元格为这k个单元格的一个子集z，而最后一个单元格由前面k-1个单元格的值决定。所以，我们只需要画$z|\tilde{x}$。
我们设C为粗化矩阵，其中C的每一行代表一个粗像素，每一列代表一个细像素，对于前文讲的成像的例子，如果将细像素聚合为$C_{ij}=1$(求和操作)；所以说，${\tilde{x}}^{\ast }=Cx$，我们提出的粗像素${\tilde{x}}^{\ast }$是当前细像素的一个线性变换。而增广矩阵$\tilde{C}$是在一列中加入数行零和一的满秩矩阵，该列对应于一组中的一个细像素(最后一列除外)。比如说，本文的两个例子中，都是每四个细像素对应一个粗像素，对于每一个粗像素，$\tilde{C}$中添加三行，这样就可以从这四行中恢复出细像素，所以从x变换到$\tilde{C}x$就没有信息损失了。而且我们现在知道了：

所以说我们知道了$\tilde{x}$和$z$的联合概率分布。我们记W为精度矩阵：


由此我们就可以得到条件分布$z|\tilde{x}$。但是，这个绘制出来的每个z图像只包含三个单元格，所以需要对每组的最后一个单元格的值进行扩充就可以得到完整的$x^{\ast }$图像.(PRML p63-65)

(2)、APPENDIX C
顺序的粗到细的更新
下面先对swapping 提议的顺序算法做一个概要：
1）通过对细链中相应的单元进行求和或者平均，来构造一个粗略的提议；
2）创建细提议的第一个阶段，通过将粗单元格对应的细单元格设置为等于$m/\tilde{m}$乘以之前粗单元格的值。
3）对于每一个粗单元格，从多元正态分布(由先验MRF定义)中提取相应的细单元格的联合样本。条件是这些细单元格的和或者均值等于粗单元格的值。
4）从完整的条件分布中采样粗尺度和细尺度，并且独立的采样建议值${\theta }_y^{\ast }$和${\tilde{\theta }}_y^{\ast }$。下面的例子并没有对${\theta }_y^{\ast }$和${\tilde{\theta }}_y^{\ast }$进行更新。