线性模型
用一条线拟合实际数据:h(θ)=θ0x0+θ1x1+...+θnxnh(\theta)=\theta_{0}x_{0}+\theta_{1}x_{1}+...+\theta_{n}x_{n}h(θ)=θ0x0+θ1x1+...+θnxn
这里,将h(θ)h(\theta)h(θ) 称为假设函数,是对实际值的一种估计,是估计就会有偏差,我们的目标是尽量的找到估计值与实际值之间的误差最小的拟合线,这样可以使用拟合线预测未知数据。
利用最小二乘法构建损失函数
损失函数:J(θ)=12N∑i=1N(hθ(x(i))−y(i))2J(\theta)=\frac{1}{2N}\sum_{i=1}^{N}(h_{\theta}(x^{(i)})-y^{(i)})^2J(θ)=2N1∑i=1N(hθ(x(i))−y(i))2
以单变量线性模型为例,下图表示θ0=0\theta_{0}=0θ0=0时,不同的θ1\theta_{1}θ1值的拟合线与真实值之间的关系, 最好的拟合线是橘色线,即斜率为2.
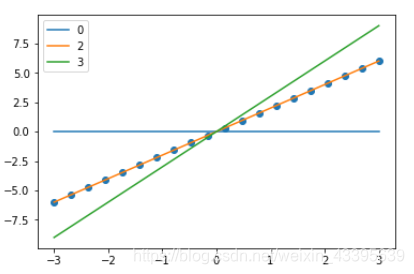
- 当θ1=0<2\theta_{1}=0< 2θ1=0<2(最佳拟合)时,估计值与真实值差距大,损失函数值大
- 当θ1=3>2\theta_{1}=3>2θ1=3>2(最佳拟合)时,估计值与真实值差距大,损失函数值大
- 即,损失函数在最佳取值左右两侧都会比较大
损失函数随θ\thetaθ的变化情况:
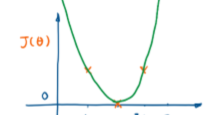
梯度下降法优化损失函数
梯度下降的方式是在不知道最优参数时,初始化一个参数值,然后不断优化,在找最小值的过程中沿着负梯度(一阶导)的方向下降最快,因此沿着这个方向走。方向确定好,确定向前走的步长(学习率)。
-
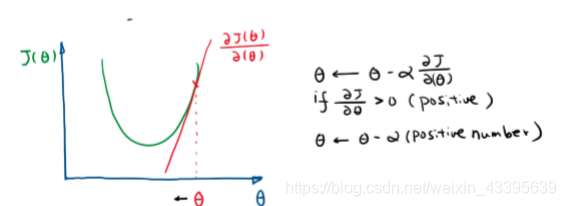
梯度对优化的影响:
- 初始值在最优点右侧时,负梯度<0,步长α\alphaα>0,更新参数时,参数向减小的方向移动。
- 初始值在最优点左侧时,负梯度>0,步长α\alphaα>0,更新参数时,参数向增加的方向移动。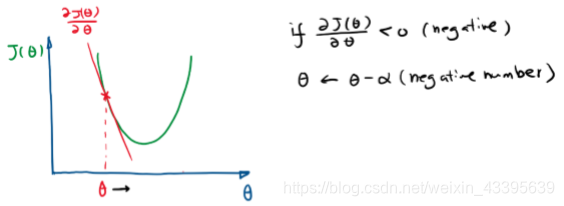
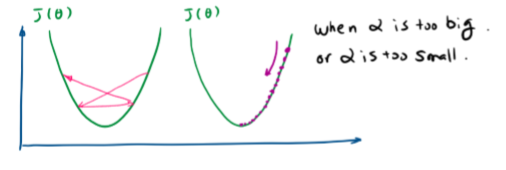
- 步长对优化的影响
- 步长α\alphaα过大,可能造成不收敛,左图
- 步长α\alphaα过小,优化速度会比较慢
推广到多变量线性模型,梯度下降对参数的更新:
- θj:=θj−α∂J(θ)∂θj\theta j := \theta j - \alpha \frac{\partial J(\theta)}{\partial \theta j}θj:=θj−α∂θj∂J(θ)
- 线性模型:θj:=θj−α1N∑i=1N(hθ(x(i)−y(i))xj(i))\theta j := \theta j - \alpha \frac{1}{N} \sum_{i=1}^{N}(h_{\theta}(x^{(i)}-y^{(i)})x_{j}^{(i)})θj:=θj−αN1∑i=1N(hθ(x(i)−y(i))xj(i))
- 梯度下降对参数的更新要所有参数一起更新。即每轮更新成新的hθ(X)h_{\theta}(X)hθ(X),假设函数中,每个参数都更新,再进行下一轮。
当然不仅仅是线性模型可以用梯度下降的方式进行优化,很多其他的数学模型也都可以用梯度下降的方法进行优化。梯度下降是一类优化的方法。
【小结】想要求得最能拟合真实数据的线性模型,可以先设置一个初始值,用最小二乘法构造损失函数,通过梯度下降的优化方法不断更新参数,使其达到最优。
直接计算最优解
梯度下降的方式,需要通过不断迭代找到最优解,那能否通过直接找到最优解的位置呢?对凸函数来说,一阶导为0处,就是一个可直接计算出的最优解。
h(θ)=θ0x0+θ1x1+...+θnxnh(\theta)=\theta_{0}x_{0}+\theta_{1}x_{1}+...+\theta_{n}x_{n}h(θ)=θ0x0+θ1x1+...+θnxn
- 模型共有n个特征,N个样本数据,y(i)y^(i)y(i)是预测值。
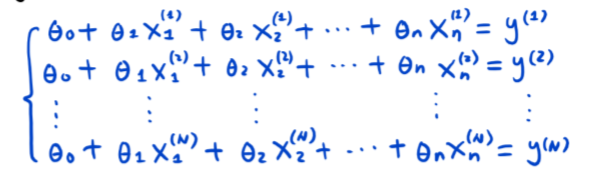
- 用矩阵可以表示为
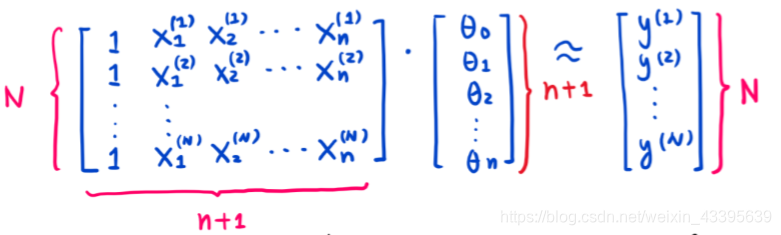
用X是(n+1)xN维特征矩阵,θ\thetaθ是(n+1)维参数列向量,XθX\thetaXθ是N维列向量(估计值)。Y是N维列向量(真实值)。
最小二乘法 构造损失函数
min∣∣Xθ−Y∣∣22min ||X\theta -Y||_{2}^{2}min∣∣Xθ−Y∣∣22 L-2距离的平方:即各项平方和
令∂S∂θ=0\frac{\partial S}{\partial \theta}=0∂θ∂S=0 ,得θ=(XTX)−1XTY\theta=(X^{T}X)^{-1}X^{T}Yθ=(XTX)−1XTY
- 推导过程
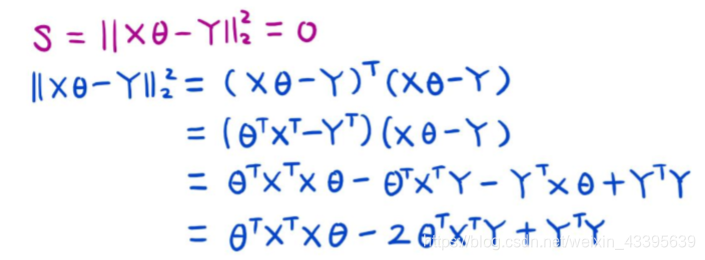
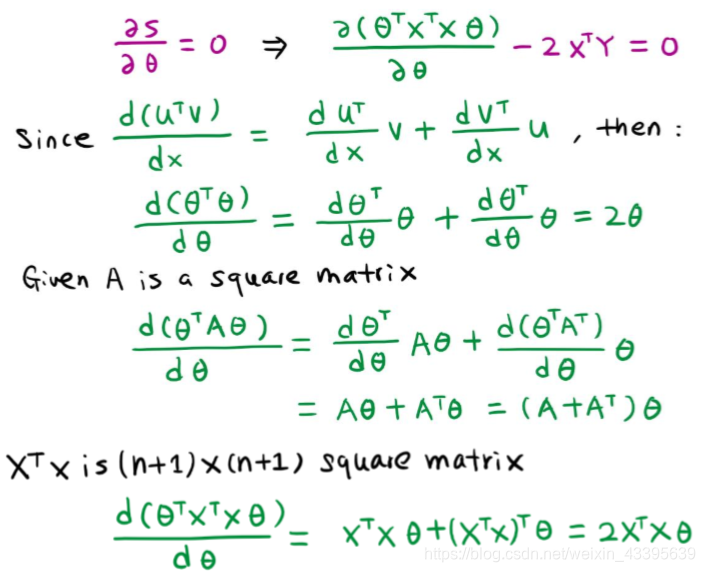
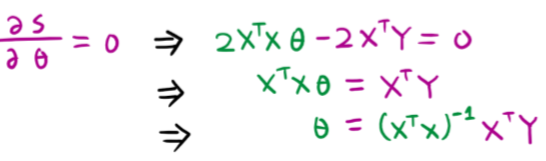





 本文探讨了线性模型的构建与优化,通过最小二乘法构建损失函数,并运用梯度下降法寻找最佳参数,实现对真实数据的精确拟合。
本文探讨了线性模型的构建与优化,通过最小二乘法构建损失函数,并运用梯度下降法寻找最佳参数,实现对真实数据的精确拟合。
















 548
548

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








