转载至:http://blog.sina.com.cn/s/blog_531bb76301017ply.html
梯度下降法
描述
梯度下降法,基于这样的观察:如果实值函数  在点
在点 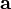 处可微且有定义,那么函数
处可微且有定义,那么函数  在
在 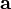 点沿着梯度相反的方向
点沿着梯度相反的方向  下降最快。
下降最快。
因而,如果
对于  为一个够小数值时成立,那么
为一个够小数值时成立,那么 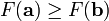 。
。
考虑到这一点,我们可以从函数  的局部极小值的初始估计
的局部极小值的初始估计  出发,并考虑如下序列
出发,并考虑如下序列  使得
使得
因此可得到
如果顺利的话序列 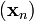 收敛到期望的极值。注意每次迭代步长
收敛到期望的极值。注意每次迭代步长  可以改变。
可以改变。
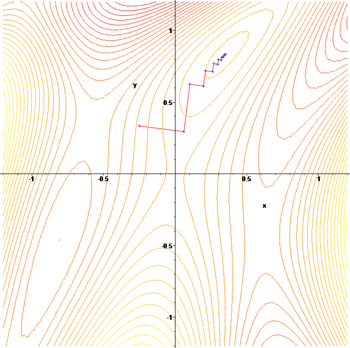
右侧的图片示例了这一过程,这里假设  定义在平面上,并且函数图像是一个碗形。蓝色的曲线是等高线(水平集),即函数
定义在平面上,并且函数图像是一个碗形。蓝色的曲线是等高线(水平集),即函数  为常数的集合构成的曲线。红色的箭头指向该点梯度的反方向。(一点处的梯度方向与通过该点的等高线垂直)。沿着梯度下降方向,将最终到达碗底,即函数
为常数的集合构成的曲线。红色的箭头指向该点梯度的反方向。(一点处的梯度方向与通过该点的等高线垂直)。沿着梯度下降方向,将最终到达碗底,即函数  值最小的点。
值最小的点。
例子
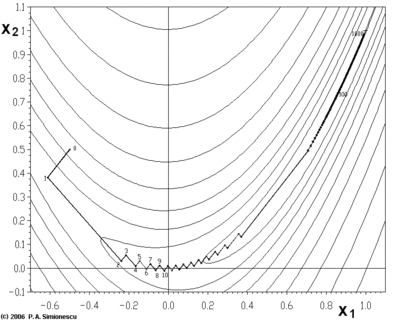
梯度下降法处理一些复杂的非线性函数会出现问题,例如Rosenbrock函数
其最小值在 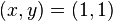 处,数值为
处,数值为 。但是此函数具有狭窄弯曲的山谷,最小值
。但是此函数具有狭窄弯曲的山谷,最小值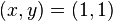 就在这些山谷之中,并且谷底很平。优化过程是之字形的向极小值点靠近,速度非常缓慢。
就在这些山谷之中,并且谷底很平。优化过程是之字形的向极小值点靠近,速度非常缓慢。
下面这个例子也鲜明的示例了"之字"的下降,这个例子用梯度下降法求  的极小值。
的极小值。
缺点
由上面的两个例子,梯度下降法的缺点是 [1]:
- 靠近极小值时速度减慢。
- 直线搜索可能会产生一些问题。
- 可能会'之字型'地下降。
共轭梯度法的推导
的迭代方法。共轭梯度法可以从不同的角度推导而得,包括作为求解最优化问题的共轭方向法的特例,以及作为求解特征值问题的 Arnoldi/Lanczos 迭代的变种。
本条目记述这些推导方法中的重要步骤。
从共轭方向法推导
从 Arnoldi/Lanczos 迭代推导
共轭梯度法可以看作 Arnoldi/Lanczos 迭代应用于求解线性方程组时的一个变种。
一般 Arnoldi 方法
Arnoldi 迭代从一个向量  开始,通过定义
开始,通过定义  ,其中
,其中
逐步建立 Krylov 子空间
的一组标准正交基  。
。
换言之,对于  ,
, 由将
由将  相对于
相对于  进行 Gram-Schmidt 正交化然后归一化得到。
进行 Gram-Schmidt 正交化然后归一化得到。
写成矩阵形式,迭代过程可以表示为
其中
当应用于求解线性方程组时,Arnoldi 迭代对应于初始解  的残量
的残量  开始迭代,在每一步迭代之后计算
开始迭代,在每一步迭代之后计算  和新的近似解
和新的近似解  .
.
直接 Lanzcos 方法
在余下的讨论中,我们假定  是对称正定矩阵。由于
是对称正定矩阵。由于  的对称性, 上 Hessenberg 矩阵
的对称性, 上 Hessenberg 矩阵  变成对阵三对角矩阵。于是它可以被更明确地表示为
变成对阵三对角矩阵。于是它可以被更明确地表示为
这使得迭代中的  有一个简短的三项递推式。Arnoldi 迭代从而简化为 Lanczos 迭代。
有一个简短的三项递推式。Arnoldi 迭代从而简化为 Lanczos 迭代。
由于  对称正定,
对称正定, 同样也对称正定。因此,
同样也对称正定。因此, 可以通过不选主元的 LU 分解分解为
可以通过不选主元的 LU 分解分解为
其中  和
和  有简单的递推式:
有简单的递推式:
改写  为
为
其中
此时需要观察到
实际上, 和
和  同样有简短的递推式:
同样有简短的递推式:
通过这个形式,我们得到 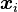 的一个简单的递推式:
的一个简单的递推式:
以上的递推关系立即导出比共轭梯度法稍微更复杂的直接 Lanczos 方法。
从正交性和共轭性导出共轭梯度法
如果我们允许缩放  并通过常数因子补偿缩放的系数,我们可能可以的到以下形式的更简单的递推式:
并通过常数因子补偿缩放的系数,我们可能可以的到以下形式的更简单的递推式:
作为简化的前提,我们现在推导  的正交性和
的正交性和  的共轭性,即对于
的共轭性,即对于 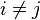 ,
,
各个残量之间满足正交性的原因是  实际上可由
实际上可由  乘上一个系数而得。这是因为对于
乘上一个系数而得。这是因为对于  ,
, ,对于
,对于  ,
,
要得到  的共轭性,只需证明
的共轭性,只需证明  是对角矩阵:
是对角矩阵:
是对称的下三角矩阵,因而必然是对角矩阵。
现在我们可以单纯由 的正交性和
的正交性和  的共轭性推导相对于缩放后的
的共轭性推导相对于缩放后的  的常数因子
的常数因子 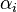 和
和 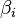 。
。
由于  的正交性,必然有
的正交性,必然有  。于是
。于是
类似地,由于  的共轭性,必然有
的共轭性,必然有  。于是
。于是
推导至此完成。
参考文献
- Hestenes, M. R.; Stiefel, E.. Methods of conjugate gradients for solving linear systems (PDF). Journal of Research of the National Bureau of Standards. 12 1952,49 (6).
- Saad, Y.. Chapter 6: Krylov Subspace Methods, Part I. Iterative methods for sparse linear systems. 2nd. SIAM. 2003. ISBN
978-0898715347.






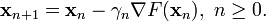
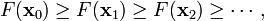


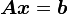



































 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








