【数据结构与算法】(12)：插入排序算法：直接插入排序和希尔排序_若待排序序列在排序前已按关键字递增排列,则采用( )方法比较次数最多-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_43382136/article/details/136688981

本文详细介绍了插入排序的两种形式：直接插入排序和希尔排序。直接插入排序适用于小规模数据，通过逐步插入元素来构建有序序列；希尔排序则是对直接插入排序的优化，通过预排序减少关键字比较和移动次数。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

🤡博客主页：醉竺

🥰本文专栏：《数据结构与算法》

😻欢迎关注：感谢大家的点赞评论+关注，祝您学有所成！

✨✨💜💛想要学习更多数据结构与算法点击专栏链接查看💛💜✨✨

1. 排序的概念和应用

无论是日常生活还是很多科学领域当中，排序都是会经常面对的问题，比如按成绩对学校的学生排序，按薪水多少对公司员工排序等。

我将按照对 数据操作方式 的不同来分类讲解。这里先给你提供一个思维导图。

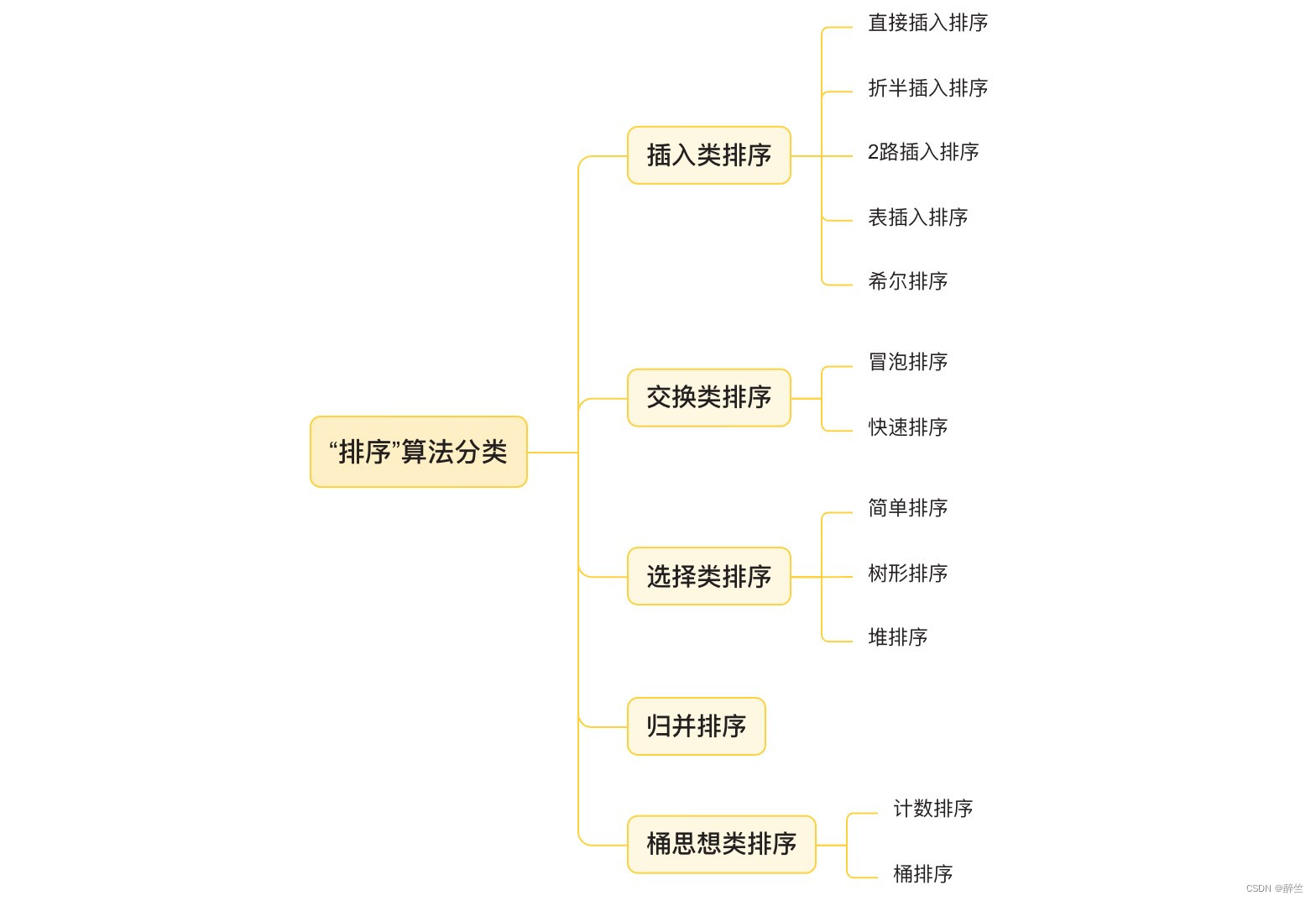
在讲解具体的排序算法之前，我们先一起看一些它的基本概念。

排序的概念和特性

排序：所谓排序（Sort），就是将一组数据（也称元素），按照一定的规则调换位置，使这组数据按照递增或递减的顺序重新排列。例如数据库中有一个“学生表”，可以针对该表中的“年龄”字段进行排序，那么这个待排序的字段就称为键（key）或者关键字。排序一般是为了让查找数据的效率变得更高。

这里涉及一个 排序算法的稳定性问题 。依旧以“学生表”为例，假如表中数据如下：

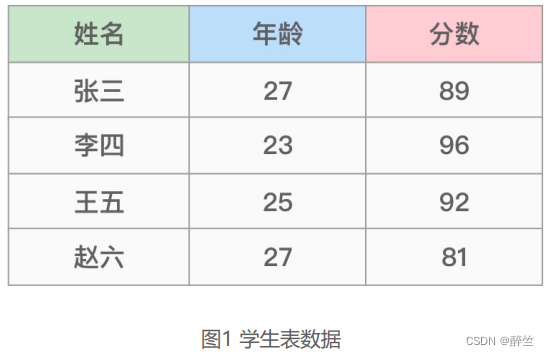
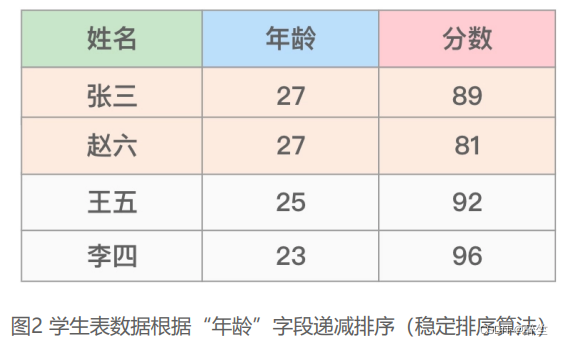
在图1所示的学生表中，需要针对表中的“年龄”字段（键）按照某种排序算法进行递减或者递增排序。此时（排序前）张三和赵六的年龄都是27岁且张三这条记录位于赵六之前，而在排序后，如果张三这条记录依旧位于赵六之前，那我们就说这种排序算法是稳定的，如图2所示：

反之，如果排序后赵六这条记录位于张三之前，那我们就说这种排序算法是不稳定的，如图3所示：

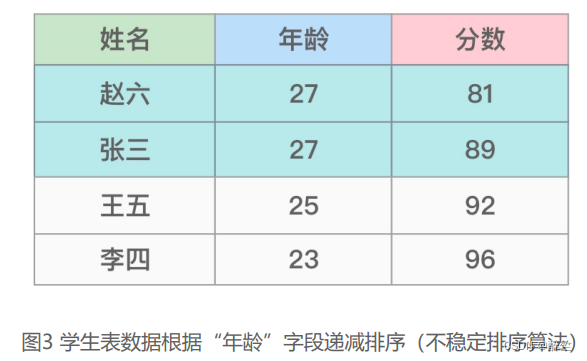
所以，所谓 稳定的排序算法，指的就是关键字相同的元素在排序后相对位置不变。

稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。

针对排序算法的稳定性有两点说明：

有些排序算法，基于其实现的原理，确实是无法做到稳定，这种算法当然称为不稳定。

有些排序算法，是可以做到稳定的。但是，如果稍微调整一下它的实现代码，让它变得不稳定也是很容易的。当然，当无法判断一个算法是否稳定时，可以书写测试代码来进行稳定性测试，我也会根据需要提供测试范例。

在后续讲解排序算法时，虽然很多时候都是用整数进行举例，但在真正的项目中，往往要排序的并不是单纯的数字，而是一组对象，按照对象的某个关键字来排序，所以排序的稳定性也是一个必须要考虑的问题。

根据在排序过程中待排序的数据是否全部被载入到内存中，排序分为 内部排序（内排序）和外部排序（外排序）。接下来介绍的各种排序算法涉及的主要是内部排序，包含各种经典的内部排序算法。

内部排序：是指在整个排序过程中，待排序的所有数据（记录）都被载入到内存中。

外部排序：是指在整个排序过程中，因为排序的数据太多（比如大数据）而不能同时载入到内存中，导致整个的排序过程需要在内存和外存（比如磁盘）之间进行多次数据交换。因为磁盘和内存的读写速度相比往往要慢上数十甚至数百倍，所以外部排序往往需要尽量减少磁盘的读写次数。

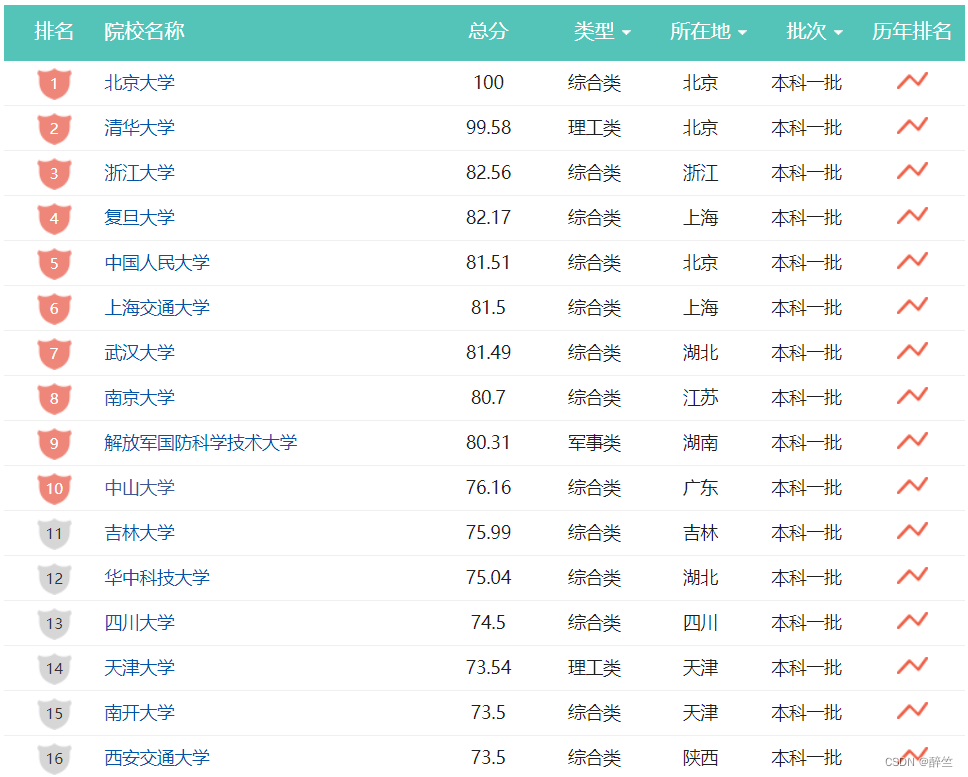
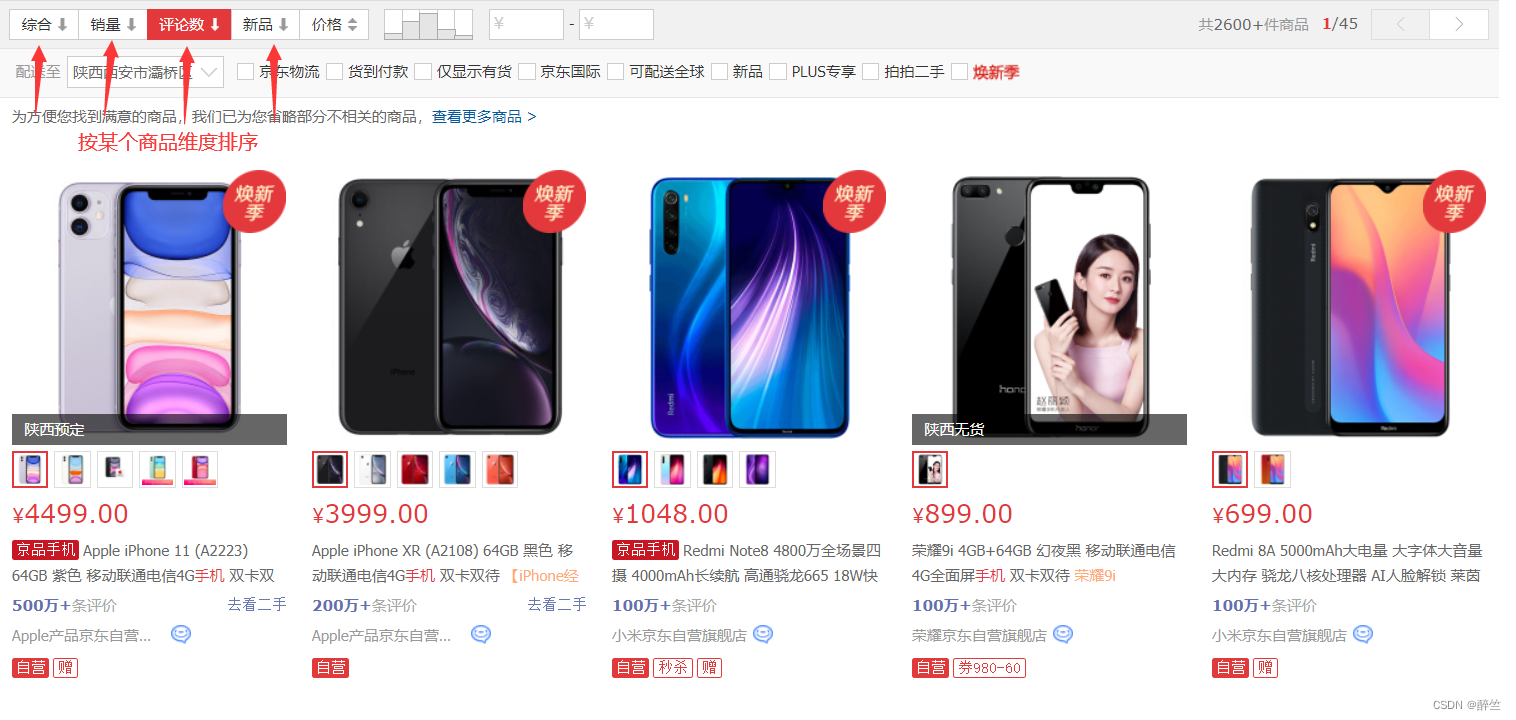
排序的运用

2. 插入排序

插入排序思想

所谓 插入类 排序，就是向有序序列（已经排好序的序列）中依据关键字的比较结果寻找合适的位置，插入新的记录，构成新的有序序列，直至所有记录插入完毕。

实际中我们玩扑克牌时，就用了插入排序（直接插入排序）的思想：

直接插入排序过程

插入类排序可以细分为很多种，每种之间的差别主要体现在插入位置的查找以及插入新数据导致原有数据的移动方面。这一小节，先看一种简单粗暴但是好理解的插入类排序方式——直接插入排序。

直接插入排序：这种算法的思想是每次将一个记录按其关键字的大小插入到已经排好序的序列中，直至全部记录插入完毕。这种排序方式将待排数据依次和数组中已经排好序的记录进行比较并确定自己的位置。

下面是直接插入排序的两个动态图：

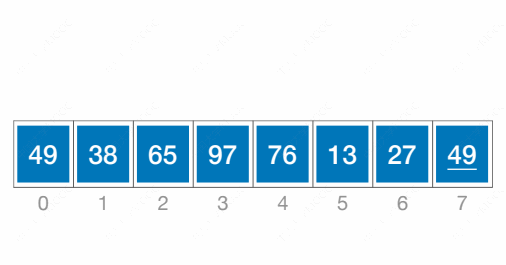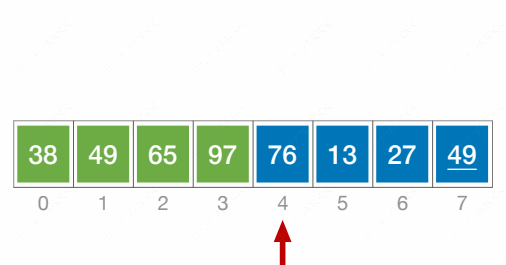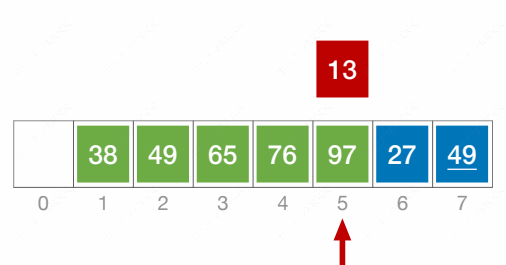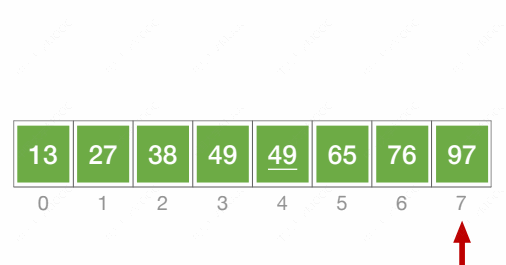
插入排序代码

//直接插入排序（从小到大）
template<typename T>//T代表数组元素类型
void InsertSort(T myarray[], int length) //myarray：要排序的数组元素，length：数组中元素数量
{
	if (length <= 1) //不超过1个元素的数组，没必要排序
		return;

	for (int i = 1; i < length; ++i) //从第2个元素（下标为1）开始比较
	{
		if (myarray[i] < myarray[i - 1])
		{
			T temp = myarray[i];   //暂存myarray[i]值，防止后续移动元素时值被覆盖
			int j;
			for (j = i - 1; j >= 0 && myarray[j] > temp; --j) //检查所有前面排好序的元素
			{
				myarray[j + 1] = myarray[j]; //所有大于temp的元素都向后移动
			}
			myarray[j + 1] = temp; //复制数据到插入位置，注意j因为被减了1，这里加回来
		}
	return;
}

时间复杂度分析

从代码中可以看到，直接插入排序实现代码比较简单。因为只有一些临时变量参与运算，所以其空间复杂度为O(1)。
对于时间复杂度方面，主要来自于关键字比较和位置移动操作。对于具有n个元素的数组，外循环次数是n-1次。
在最好的情况下，即数组中元素已经是有序的情况下，外循环需要循环n-1次，每次也只需要一次关键字比较（if (myarray[i] < myarray[i - 1])语句），不需要进行任何元素移动，所以，最好情况时间复杂度为O( $n$ )。
在最坏情况下，即数组中元素正好是逆序排列的情况下，外循环需要循环n-1次，每次循环都要比较和移动元素若干次，所以最坏情况时间复杂度为O( $n^{2}$ )。平均情况时间复杂度也为O( $n^{2}$ )。
此外，从实现代码中不难看到，即使遇到了关键字相同的两条记录，这两条记录的相对顺序也不会发生改变，所以这个排序算法是稳定的。
直接插入排序比较适合待排序记录数量比较少时的情形，如果待排序记录的数量比较大，就要考虑通过减少比较和移动数据次数对这种排序实现方法进行优化。下面，我们会看一看优化（改进）的插入排序算法（希尔排序）。

直接插入排序的特性总结：

元素集合越接近有序，直接插入排序算法的时间效率越高

时间复杂度：O(N^2)

空间复杂度：O(1)，它是一种稳定的排序算法

稳定性：稳定

3. 希尔排序

希尔排序这个名字来源于它的发明者希尔（Donald Shell），这类排序也被称作“缩小增量排序（Diminishing Increment Sort）”，是直接插入排序的一种更高效率的改进版。

根据直接据插入排序的特点，思考如何对其优化？

首先，在待排序的数组中，元素本身就是有序的情况下，就不需要移动任何元素，所以直接插入排序最好情况时间复杂度为O(n)。不难想象，如果数组中元素多数都是有序（基本有序）的情况下，那么需要移动的元素数量就会大大减少。
其次，这里所谈到的基本有序，可以理解成小的关键字大部分在前面，大的关键字大部分在后面，比如这个数组中的元素{1,2,10,16,18,45,23,99,42,67} 和 {16,1,45,23,99,2,18,67,42,10}数组中元素相比，前者算得上是基本有序了。
最后，如果数组中元素数量较少，那么直接插入排序的效率也会很高。

基于上述思考，对直接插入排序算法进行改进，就可以得到希尔排序算法。

希尔排序思想

先追求元素的部分有序，然后再逐渐逼近全局有序。即：
先将整个待排序记录序列（或称为数组元素）分割成若干个子序列，分别进行直接插入排序，等到整个序列中的记录基本有序时，再对所有记录进行一次直接插入排序。

希尔排序会进行多趟排序，每趟排序会设置一个增量，这里注意，这个增量初始值到底是多大才合适并没有公论，感兴趣的可以阅读一下2.4小节的拓展阅读。

接下来的例子中，我将“数组中元素数量 / 2”作为增量的初始值。

以数组{1,2,10,16,18,45,23,99,42,67}为例，来说明希尔排序。

数组中的元素有10个，所以增量初值可以设置为5。第一趟排序，把距离为5的元素划分到一个子序列中，并对这个子序列中的元素从小到大排序。参考图1：

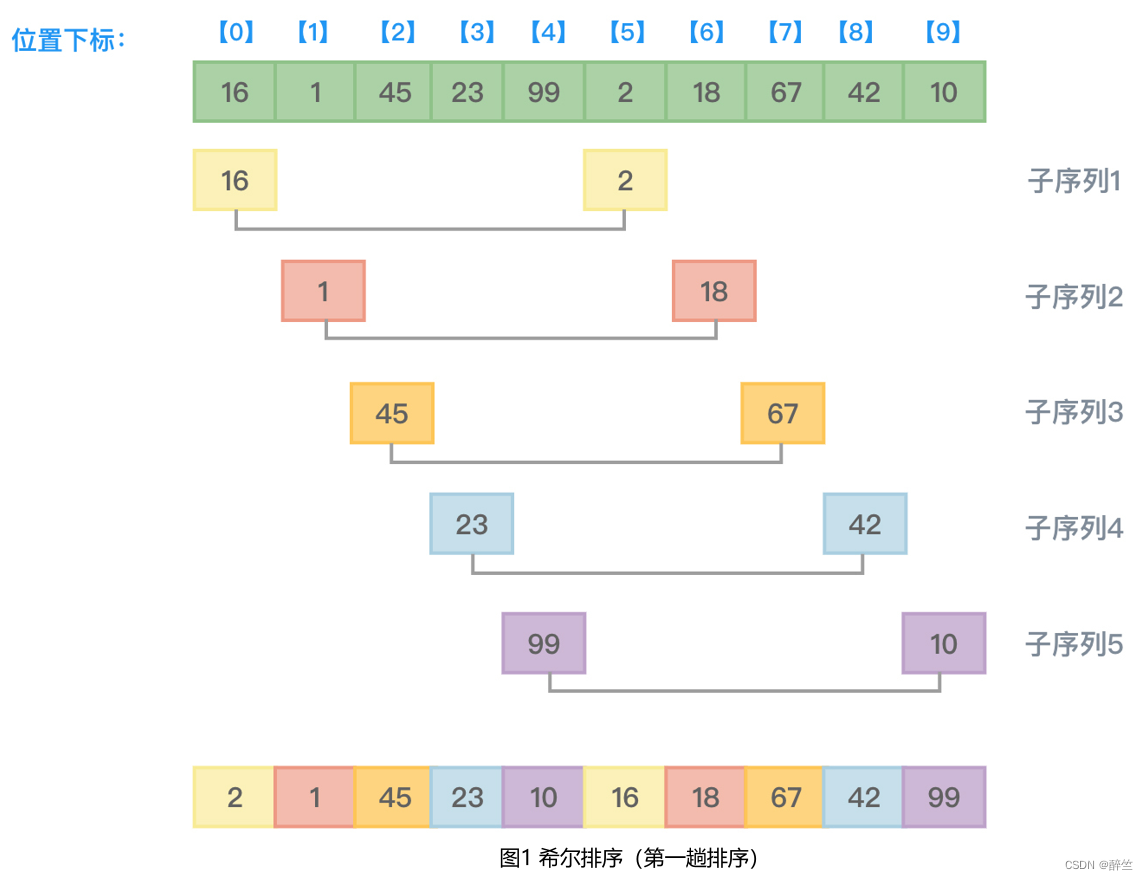
从图1可以看到，第一趟排序，因为增量值是5，这意味着即将排序的元素间隔5个位置。所以下标为0的元素16和下标为5的元素2需要进行大小比较，并根据从小到大的顺序决定谁在前谁在后。

因为2比16小，所以2应该在前，也就是16和2互换位置。接着，有元素1和18、元素45和67、元素23和42、元素99和10依次进行大小比较并排序，本趟排序得到的结果数组元素值为{2,1,45,23,10,16,18,67,42,99}。

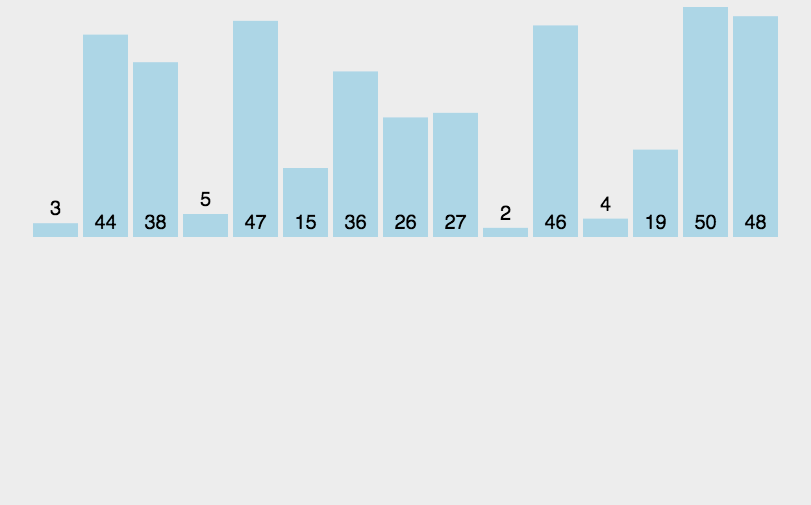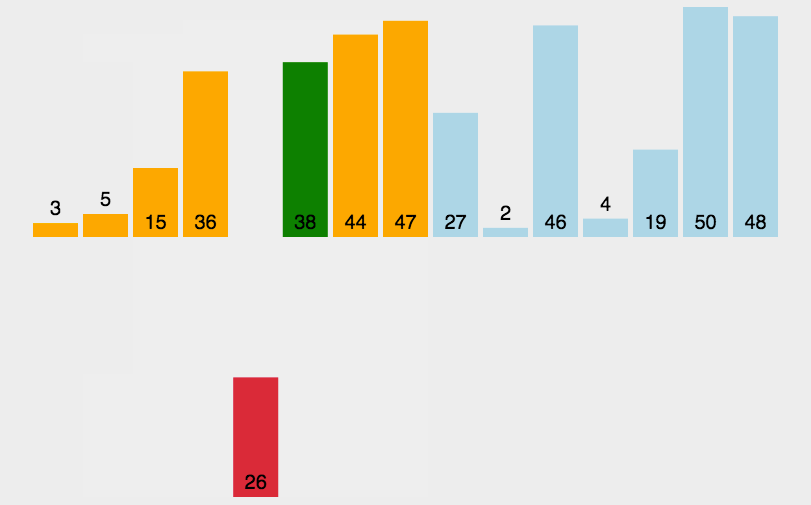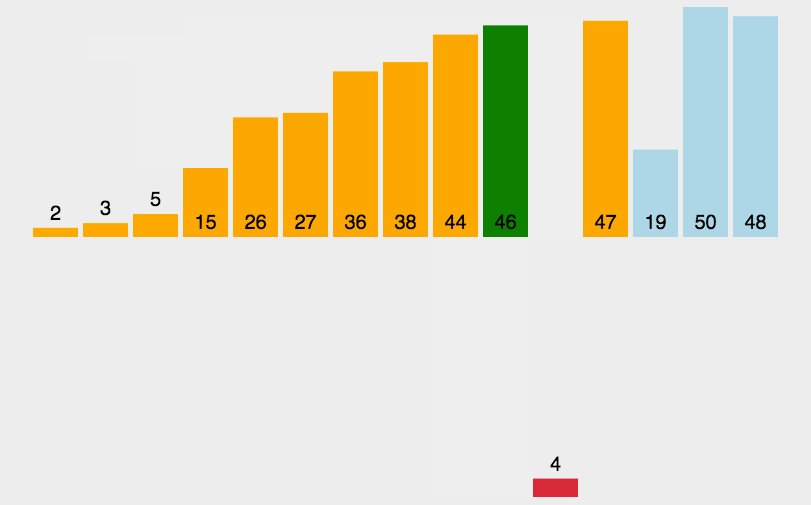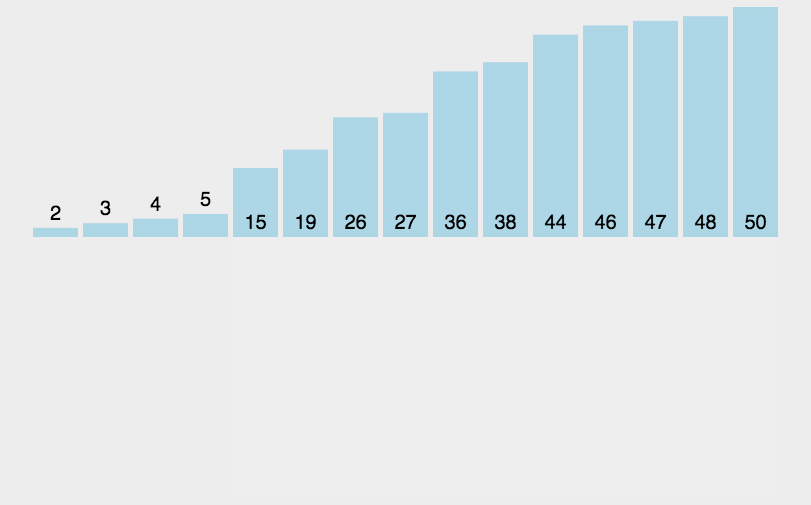
第二趟排序，要缩小增量的值，比如可以每次缩小一半（希尔本人这样建议），也就是：增量=增量/2，原来增量的值是5，这次增量的值就变成了2，即把距离为2的元素划分到一个子序列中并对该子序列中的元素从小到大排序。参考图2：

从图2可以看到，第二趟排序因为增量值是2，意味着即将排序的元素间隔2个位置。所以下标为0的元素2、下标为2的元素45、下标为4的元素10、下标为6的元素18、下标为8的元素42进行大小比较并根据从小到大的顺序决定谁在前谁在后。最终得到2、10、18、42、45的顺序。

同理，元素1、23、16、67、99从小到大排序，本趟排序得到的结果数组元素值为{2,1,10,16,18,23,42,67,45,99}。可以看到，每一趟排序，都使数组中的元素更进一步基本有序。

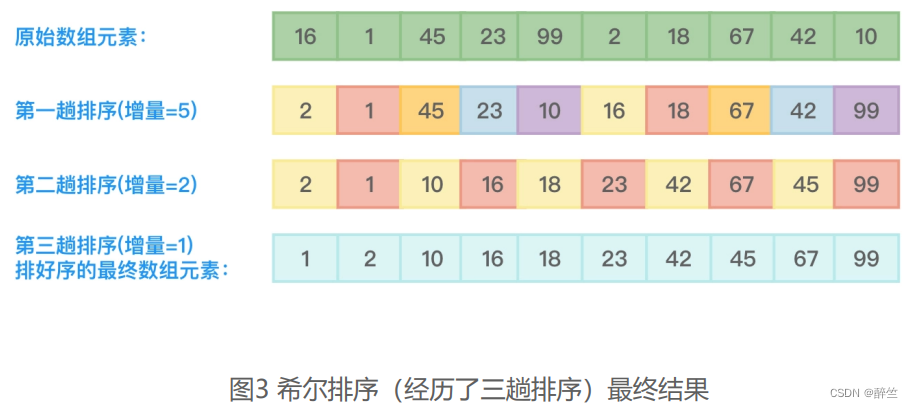
第三趟排序，继续缩小增量的值，增量=增量/2，原来增量的值是2，这次增量的值就变成了1。这就意味着要对数组中的所有元素进行从小到大的直接插入排序，增量值为1后的排序也是最后一次排序。最终数组元素的值就变成了{1,2,10,16,18,23,42,45,67,99}。所以，一共进行了三趟排序，得到了最终排好序的数组元素。参考图3：

希尔排序代码

//希尔排序（从小到大）
template<typename T>
void ShellSort(T myarray[], int length)
{
	if (length <= 1) //不超过1个元素的数组，没必要排序
		return;

	int Dim = length / 2; // Dim：增量，取值分别为7、3、1
	while (Dim >= 1)
	{
		// 从 myarray[Dim] 开始，向后遍历数组。
        // 对于每个元素 myarray[i]，我们将其与 Dim 间隔之前的元素进行比较和插入排序。
		for (int i = Dim; i < length; ++i) //i值每次改变可以处理到不同的子序列
		{
			if (myarray[i] < myarray[i - Dim])
			{
				T temp = myarray[i];//暂存myarray[i]值，防止后续移动元素时值被覆盖
				int j;
				for (j = i - Dim; j >= 0 && myarray[j] > temp; j -= Dim) //检查所有前面排好序的元素
				{
					//所有大于temp的元素都向后移动
					myarray[j + Dim] = myarray[j]; //大于temp的元素都向后移动
				}
				myarray[j + Dim] = temp; //复制数据到插入位置，注意j因为被减了Dim，这里加回来
			}
		}
		
		Dim /= 2; //Dim减半，继续下一趟排序
	}
	return;
}

从代码中可以看到，希尔排序实现代码的空间复杂度为O(1)。而对于时间复杂度的分析，本算法则显得比较复杂。当采用不同的增量序列，比如上面代码中每次增量减少为原来的一半时，希尔排序的总趟数会不同，而且每趟排序元素对比次数和元素移动次数都可能会受到影响。所以希尔排序的时间复杂度目前为止还无法用数学手段确切地证明。

但如果增量的初值直接设置为1的话，那么希尔排序会退化为直接插入排序，这时的时间复杂度是希尔排序的最坏时间复杂度即O( $n^{2}$ )。如果待排序元素的数量在一定的范围内，那么时间复杂度可以达到O( $n^{1.3}$ )，平均时间复杂度为O( $nlog_{2}^{n}$ )，这意味着希尔排序算法优于直接插入排序算法。

此外，希尔排序算法是不稳定的，这不难证明。试想一下具有3个元素99、10、10的数组，因为增量值的设定并没有公论，所以如果设定第一趟排序增量值为2，第二趟排序增量值为1，那么后面两个都是10的数组元素位置就会发生改变，也就是图6的样子。

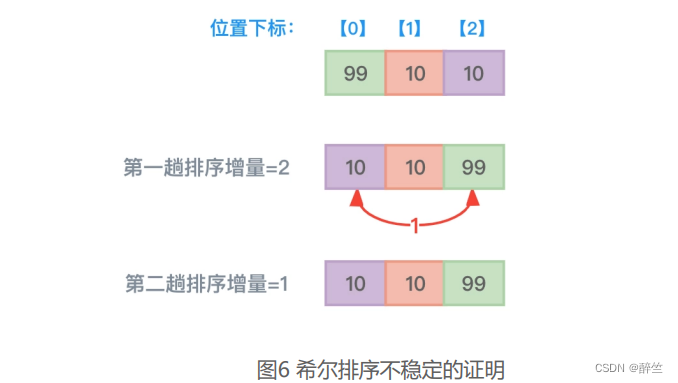
上图中，第一趟排序元素99和最末尾的元素10进行了位置交换，而第二趟排序并没有做任何数组元素位置的交换。但显而易见，原下标为2的数组元素10被移动到了下标为0的位置，跑到了下标为1的数组元素10之前。所以，希尔排序算法是不稳定的。

希尔排序的特性总结：

希尔排序是对直接插入排序的优化。
当gap > 1时都是预排序，目的是让数组更接近于有序。当gap == 1时，数组已经接近有序的了，这样就会很快。这样整体而言，可以达到优化的效果。我们实现后可以进行性能测试的对比。
希尔排序的时间复杂度不好计算，因为gap的取值方法很多，导致很难去计算，因此在好些书中给出的希尔排序的时间复杂度都不固定：
稳定性：不稳定