朴素贝叶斯(naive Bayes)法是基于贝叶斯定理与特征条件独立假设的分类方法。对于给定的训练数据集,首先基于特征条件独立假设学习输入/输出的联合概率分布;然后基于此模型,对给定的输入 x,利用贝叶斯定理求出后验概率最大的输出 y。朴素贝叶斯法实现简单,学习与预测的效率都很高,是一种常用的方法。实际上学习到生成数据的机制,所以属于生成模型。
概率论基本知识
- 联合概率:设 A,B 是两个随机事件,A 和 B 同时发生的概率称为联合概率,记为:P(AB)。
- 条件概率:在 B 事件发生的条件下,A 事件发生的概率称为条件概率,记为:P(A|B),P(A|B) = P(AB) / P(B)。
- 乘法定理:P(AB) = P(BA) = P(B)P(A|B) = P(A)P(B|A)。
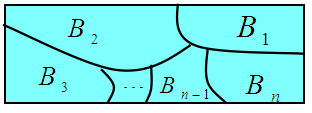
【样本空间划分】:设 Ω \Omega Ω 为试验 E 的样本空间, B 1 , B 2 , … , B n B_1, B_2, \ldots, B_n B1,B2,…,Bn 为 E 的一组事件,若
- B i B j = ∅ , i , j = 1 , 2 , … , n B_iB_j = \emptyset, \quad i, j = 1,2,\ldots,n BiBj=∅,i,j=1,2,…,n
- B 1 ⋃ B 2 ⋃ … ⋃ B n = Ω B_1 \bigcup B_2 \bigcup \ldots \bigcup B_n = \Omega B1⋃B2⋃…⋃Bn=Ω
则称 B 1 , B 2 , … , B n B_1, B_2, \ldots, B_n B1,B2,…,Bn 为样本空间 Ω \Omega Ω 的一个划分。
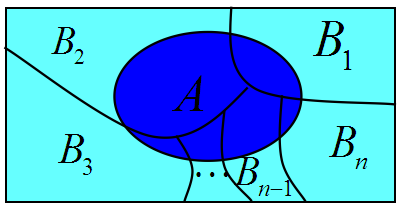
【全概率公式】:设
Ω
\Omega
Ω 为试验 E 的样本空间,A 为 E 的事件,
B
1
,
B
2
,
…
,
B
n
B_1, B_2, \ldots, B_n
B1,B2,…,Bn 为
Ω
\Omega
Ω 的一个划分,且
p
(
B
i
)
>
0
(
i
=
1
,
2
,
…
,
n
)
p(B_i) > 0(i = 1, 2, \ldots, n)
p(Bi)>0(i=1,2,…,n),则
P
(
A
)
=
P
(
A
∣
B
1
)
P
(
B
1
)
+
P
(
A
∣
B
2
)
P
(
B
2
)
+
…
+
P
(
A
∣
B
n
)
P
(
B
n
)
=
∑
i
=
1
n
P
(
A
∣
B
i
)
P
(
B
i
)
P(A) = P(A|B_1)P(B_1) + P(A|B_2)P(B_2) + \ldots + P(A|B_n)P(B_n) \\ = \sum_{i=1}^n P(A|B_i)P(B_i)
P(A)=P(A∣B1)P(B1)+P(A∣B2)P(B2)+…+P(A∣Bn)P(Bn)=i=1∑nP(A∣Bi)P(Bi)
全概率公式的主要用途在于它可以将一个复杂事件的概率计算问题,分解为若干个简单事件的概率计算问题,最后应用概率的可加性求得最终结果。
【贝叶斯公式】:设
Ω
\Omega
Ω 为试验 E 的样本空间,A 为 E 的事件,
B
1
,
B
2
,
…
,
B
n
B_1, B_2, \ldots, B_n
B1,B2,…,Bn 为
Ω
\Omega
Ω 的一个划分,且
P
(
A
)
>
0
,
p
(
B
i
)
>
0
(
i
=
1
,
2
,
…
,
n
)
P(A) > 0, \ p(B_i) > 0(i = 1, 2, \ldots, n)
P(A)>0, p(Bi)>0(i=1,2,…,n),则
P
(
B
∣
A
)
=
P
(
A
∣
B
)
P
(
B
)
P
(
A
)
P(B|A) = \frac{P(A|B)P(B)}{P(A)}
P(B∣A)=P(A)P(A∣B)P(B)
实际上,贝叶斯公式相当于乘法公式的移项:
P
(
A
B
)
=
P
(
B
)
P
(
A
∣
B
)
=
P
(
A
)
P
(
B
∣
A
)
=
>
P
(
B
∣
A
)
=
P
(
A
∣
B
)
P
(
B
)
P
(
A
)
P(AB) = P(B)P(A|B) = P(A)P(B|A) => P(B|A) = \frac{P(A|B)P(B)}{P(A)}
P(AB)=P(B)P(A∣B)=P(A)P(B∣A)=>P(B∣A)=P(A)P(A∣B)P(B)
如果此刻,我们的任务是求
P
(
B
i
∣
A
)
P(B_i|A)
P(Bi∣A),那么又该如何实现呢?我们只需要把上式中的 B 修改为
B
i
B_i
Bi 即可。
P
(
B
i
∣
A
)
=
P
(
A
∣
B
i
)
P
(
B
i
)
P
(
A
)
P(B_i|A) = \frac{P(A|B_i)P(B_i)}{P(A)}
P(Bi∣A)=P(A)P(A∣Bi)P(Bi)
根据全概率公式,我们可将 P(A) 替换为
P
(
A
∣
B
i
)
P
(
B
i
)
P(A|B_i)P(B_i)
P(A∣Bi)P(Bi) 累加和形式。
P
(
A
)
=
∑
i
=
1
n
P
(
A
∣
B
i
)
P
(
B
i
)
P
(
B
i
∣
A
)
=
P
(
A
∣
B
i
)
P
(
B
i
)
∑
i
=
1
n
P
(
A
∣
B
i
)
P
(
B
i
)
P(A) = \sum_{i=1}^n P(A|B_i)P(B_i) \\ P(B_i|A) = \frac{P(A|B_i)P(B_i)}{\sum_{i=1}^n P(A|B_i)P(B_i)}
P(A)=i=1∑nP(A∣Bi)P(Bi)P(Bi∣A)=∑i=1nP(A∣Bi)P(Bi)P(A∣Bi)P(Bi)
看到上面的式子有一种莫名的亲切感,像极了我们将数值转换为概率的做法。例如,A、B、C、D 出现的次数分别为 1、2、3、4,我们要计算 A、B、C、D 的概率。
- P(A) = 1 / (1 + 2 + 3 + 4) = 0.1;
- P(B) = 2 / (1 + 2 + 3 + 4) = 0.2;
- P© = 3 / (1 + 2 + 3 + 4) = 0.3;
- P(D) = 4 / (1 + 2 + 3 + 4) = 0.4;
只不过贝叶斯公式是将原有的概率重新转换为新的概率。
接下来我们再聊聊先验概率和后验概率。
先验概率和后验概率
- 【先验概率】:由以往的数据分析得到的概率,称之为先验概率。举个不恰当的例子,如果有一个人经常欺负你(90%),他今天突然来找你,根据以往的经验,他极有可能会继续来欺负你。今天他欺负你的概率即为先验概率。
- 【后验概率】:得到信息之后重新加以修正的概率,称之为后验概率。继续先验概率中的例子,经常欺负你的那人今天来找你道歉,并且发誓以后洗心革面再也不做欺负人的事情。我们得到了一个新的信息——他不会再欺负你,因此可以基于这条信息去修正他欺负你的概率为零,至于他会不会反悔那就另当别论。
在贝叶斯公式中,
P
(
B
∣
A
)
=
P
(
A
∣
B
)
P
(
B
)
P
(
A
)
P(B|A) = \frac{P(A|B)P(B)}{P(A)}
P(B∣A)=P(A)P(A∣B)P(B)
- P(A):是 A 的先验概率,之所以称之为“先验”是因为它仅仅根据过往的历史信息,而不用考虑 B 的影响。放到前面的例子中就是 P(A=‘被欺负’) = 0.9。
- P(A|B):是已知 B 发生后 A 的条件概率,同时也由于 B 的影响(得到新的信息)而被称作是 A 的后验概率。放到前面的例子中就是 P(A=‘被欺负’|B=‘发誓不再欺负’) = 0,A 在新信息(发誓不再欺负)条件下对原有概率加以修正,称之为 A 的后验概率。
同理可得,P(B) 是 B 的先验概率,P(B|A) 是 B 的后验概率。
为了规范说明,在此引用《统计学习方法》的数学说明。
设输入空间
χ
⊆
R
n
\chi \subseteq R^n
χ⊆Rn 为 n 维向量的集合,输出空间为类标记集合
Y
=
{
c
1
,
c
2
,
⋯
 
,
c
k
}
Y = \{c_1, c_2, \cdots, c_k\}
Y={c1,c2,⋯,ck}。输入为特征向量
x
∈
χ
x \in \chi
x∈χ,输出为类标记
y
∈
Y
y \in Y
y∈Y。X 是定义在输入空间
χ
\chi
χ 上的随机变量,Y 是定义在输出空间 Y 上的随机变量。P(X,Y) 是 X 和 Y 的联合概率分布。训练数据集由 P(X,Y) 独立同分布产生。
T
=
{
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
⋯
 
,
(
x
N
,
y
N
)
}
T = \{(x_1, y_1), (x_2, y_2), \cdots, (x_N, y_N)\}
T={(x1,y1),(x2,y2),⋯,(xN,yN)}
朴素贝叶斯法通过训练数据集学习联合概率分布 P(X,Y)。具体地,学习:
- 先验概率分布
P ( Y = c k ) , k = 1 , 2 , ⋯   , K P(Y=c_k), \quad k=1,2,\cdots,K P(Y=ck),k=1,2,⋯,K - 条件概率分布
P ( X = x ∣ Y = c k ) = P ( X ( 1 ) = x ( 1 ) , ⋯   , X ( n ) = x ( n ) ∣ Y = c k ) , k = 1 , 2 , ⋯   , K P(X=x|Y=c_k) = P(X^{(1)} = x^{(1)}, \cdots, X^{(n)} = x^{(n)} | Y=c_k), \quad k=1,2,\cdots,K P(X=x∣Y=ck)=P(X(1)=x(1),⋯,X(n)=x(n)∣Y=ck),k=1,2,⋯,K - 联合概率分布
P ( X , Y ) = P ( X = x ∣ Y = c k ) P ( Y = c k ) P(X,Y) = P(X=x|Y=c_k) \ P(Y=c_k) P(X,Y)=P(X=x∣Y=ck) P(Y=ck)
贝叶斯定理之所以有用,是因为我们在生活中经常遇到这种情况:我们可以很容易直接得出 P(X|Y),P(Y|X) 则很难直接得出。但我们更关心 P(Y|X),贝叶斯定理就为我们打通从 P(X|Y) 获得 P(Y|X) 的道路。接下来就让我们来看一个案例。
简单案例
【情境】:今天早上出门,天上飘着许多乌云,似乎要下雨了。那天上有乌云,今天会下雨的概率 P(下雨|乌云) 是多少呢?
【条件】:
- 已知这个月天上有乌云的日子比例 P(乌云) = 0.4;
- 已知下雨天的时候,早上天上有乌云的日子比例 P(乌云|下雨) = 0.8;
- 已知这个月的下雨天的比例 P(下雨) = 0.1。
令 X = 乌云,Y = 下雨,根据贝叶斯公式:
P
(
Y
∣
X
)
=
P
(
X
∣
Y
)
P
(
Y
)
P
(
X
)
=
0.8
∗
0.1
0.4
=
0.2
P(Y|X) = \frac{P(X|Y)P(Y)}{P(X)} = \frac{0.8 * 0.1}{0.4} = 0.2
P(Y∣X)=P(X)P(X∣Y)P(Y)=0.40.8∗0.1=0.2
要知道我们是无法直接判断今天是否会下雨,但通过贝叶斯公式,我们就可以借助天上的乌云来判断今天是否会下雨。虽然最终得出的结论“即使天上有乌云,真实下雨的概率也不会高”与我们的直观感受有一定的出入,但也能作为一种判断依据。
前面这些案例都只涉及一个属性,比如我们根据是否有乌云来判断是否会下雨,但下雨明显不仅仅由是否有乌云这一个属性来决定。生活中很多东西都不是由一个属性来决定的,而是由很多因素共同决定的。下面我们就来谈谈条件概率分布。
条件概率分布
当存在多个特征同时影响分类时,即条件概率公式为:
P
(
X
=
x
∣
Y
=
c
k
)
=
P
(
X
(
1
)
=
x
(
1
)
,
⋯
 
,
X
(
n
)
=
x
(
n
)
∣
Y
=
c
k
)
,
k
=
1
,
2
,
⋯
 
,
K
P(X=x|Y=c_k) = P(X^{(1)} = x^{(1)}, \cdots, X^{(n)} = x^{(n)} | Y=c_k), \quad k=1,2,\cdots,K
P(X=x∣Y=ck)=P(X(1)=x(1),⋯,X(n)=x(n)∣Y=ck),k=1,2,⋯,K
条件概率分布具有指数级数量的参数。假设共有 n 个特征和 k 个标签值,每个特征
x
(
j
)
x^{(j)}
x(j) 有
S
j
S_j
Sj 个取值,那么参数个数为
k
∏
j
=
1
n
S
j
k \prod_{j=1}^n S_j
k∏j=1nSj。下面我们就来验证这个参数个数计算公式。
【示例-二分类问题】:对于二分类问题而言,标签值共有两项 1 或 0,假设当前数据集有两项特征,特征
x
(
1
)
x^{(1)}
x(1) 有 2 种取值,分别为 1 和 2;特征
x
(
2
)
x^{(2)}
x(2) 有 3 种取值,分别为 1、2 和 3。那么参数个数为
2
×
∏
j
=
1
2
S
j
=
2
×
(
2
×
3
)
=
12
2 \times \prod_{j=1}^2 S_j = 2 \times (2 \times 3) = 12
2×j=1∏2Sj=2×(2×3)=12
我们把每一种可能都列出来,看看其总数是否等于 12:
P
(
x
(
1
)
=
1
,
x
(
2
)
=
1
∣
Y
=
1
)
P
(
x
(
1
)
=
1
,
x
(
2
)
=
2
∣
Y
=
1
)
P
(
x
(
1
)
=
1
,
x
(
2
)
=
3
∣
Y
=
1
)
P
(
x
(
1
)
=
2
,
x
(
2
)
=
1
∣
Y
=
1
)
P
(
x
(
1
)
=
2
,
x
(
2
)
=
2
∣
Y
=
1
)
P
(
x
(
1
)
=
2
,
x
(
2
)
=
3
∣
Y
=
1
)
P
(
x
(
1
)
=
1
,
x
(
2
)
=
1
∣
Y
=
0
)
P
(
x
(
1
)
=
1
,
x
(
2
)
=
2
∣
Y
=
0
)
P
(
x
(
1
)
=
1
,
x
(
2
)
=
3
∣
Y
=
0
)
P
(
x
(
1
)
=
2
,
x
(
2
)
=
1
∣
Y
=
0
)
P
(
x
(
1
)
=
2
,
x
(
2
)
=
2
∣
Y
=
0
)
P
(
x
(
1
)
=
2
,
x
(
2
)
=
3
∣
Y
=
0
)
P(x^{(1)}=1,x^{(2)}=1|Y=1) \\ P(x^{(1)}=1,x^{(2)}=2|Y=1) \\ P(x^{(1)}=1,x^{(2)}=3|Y=1) \\ P(x^{(1)}=2,x^{(2)}=1|Y=1) \\ P(x^{(1)}=2,x^{(2)}=2|Y=1) \\ P(x^{(1)}=2,x^{(2)}=3|Y=1) \\ P(x^{(1)}=1,x^{(2)}=1|Y=0) \\ P(x^{(1)}=1,x^{(2)}=2|Y=0) \\ P(x^{(1)}=1,x^{(2)}=3|Y=0) \\ P(x^{(1)}=2,x^{(2)}=1|Y=0) \\ P(x^{(1)}=2,x^{(2)}=2|Y=0) \\ P(x^{(1)}=2,x^{(2)}=3|Y=0)
P(x(1)=1,x(2)=1∣Y=1)P(x(1)=1,x(2)=2∣Y=1)P(x(1)=1,x(2)=3∣Y=1)P(x(1)=2,x(2)=1∣Y=1)P(x(1)=2,x(2)=2∣Y=1)P(x(1)=2,x(2)=3∣Y=1)P(x(1)=1,x(2)=1∣Y=0)P(x(1)=1,x(2)=2∣Y=0)P(x(1)=1,x(2)=3∣Y=0)P(x(1)=2,x(2)=1∣Y=0)P(x(1)=2,x(2)=2∣Y=0)P(x(1)=2,x(2)=3∣Y=0)
通过列举所有可能的参数组合,可以看到在只有两项特征,且各项特征的取值数不多的情况下,都已经存在这么多的参数组合。那么,随着特征的以及特征取值数的增加,其参数组合成指数级增长。
【问】:那么要如何求解条件概率分布?
【答】:朴素贝叶斯法对条件概率分布作了条件独立性假设。由于这是一个较强的假设,朴素贝叶斯法也由此得名(“朴素”的来源)。
因此,根据链式法则和条件独立性假设,我们可以将条件概率分布拆分为
P
(
X
=
x
∣
Y
=
c
k
)
=
P
(
X
(
1
)
=
x
(
1
)
,
⋯
 
,
X
(
n
)
=
x
(
n
)
∣
Y
=
c
k
)
,
k
=
1
,
2
,
⋯
 
,
K
=
P
(
X
(
1
)
=
x
(
1
)
∣
Y
=
c
k
)
P
(
X
(
2
)
=
x
(
2
)
∣
Y
=
c
k
)
⋯
P
(
X
(
n
)
=
x
(
n
)
∣
Y
=
c
k
)
=
∏
j
=
1
n
P
(
X
(
j
)
=
x
(
j
)
∣
Y
=
c
k
)
P(X=x|Y=c_k) = P(X^{(1)} = x^{(1)}, \cdots, X^{(n)} = x^{(n)} | Y=c_k), \quad k=1,2,\cdots,K \\ = P(X^{(1)} = x^{(1)}|Y=c_k) \ P(X^{(2)} = x^{(2)}|Y=c_k) \cdots P(X^{(n)} = x^{(n)}|Y=c_k) = \prod_{j=1}^n P(X^{(j)} = x^{(j)}|Y=c_k)
P(X=x∣Y=ck)=P(X(1)=x(1),⋯,X(n)=x(n)∣Y=ck),k=1,2,⋯,K=P(X(1)=x(1)∣Y=ck) P(X(2)=x(2)∣Y=ck)⋯P(X(n)=x(n)∣Y=ck)=j=1∏nP(X(j)=x(j)∣Y=ck)
条件独立性假设使得特征之间不存在相互影响,例如:
- 晴天去露天球场打篮球(90%),雨天去露天球场打篮球(10%);
- 晴天洗澡(40%),雨天洗澡(60%);
一般来说,打完篮球之后都会洗澡(当然如果真的有人打完球不洗澡,我也没有办法),但是我们假设各个特征之间不存在依赖,求晴天去露天球场打篮球和洗澡的概率。
P
(
X
(
1
)
=
打篮球
,
X
(
2
)
=
洗澡
∣
Y
=
晴天
)
=
P
(
X
(
1
)
=
打篮球
∣
Y
=
晴天
)
P
(
X
(
2
)
=
洗澡
∣
Y
=
晴天
)
P(X^{(1)}=\text{打篮球}, X^{(2)}=\text{洗澡}|Y=\text{晴天}) = \\ P(X^{(1)}=\text{打篮球}|Y=\text{晴天}) \ P(X^{(2)}=\text{洗澡}|Y=\text{晴天})
P(X(1)=打篮球,X(2)=洗澡∣Y=晴天)=P(X(1)=打篮球∣Y=晴天) P(X(2)=洗澡∣Y=晴天)
再回到先前的示例-二分类问题例子,此时我们只需要计算
P
(
x
(
1
)
=
1
∣
Y
=
1
)
P
(
x
(
1
)
=
2
∣
Y
=
1
)
P
(
x
(
1
)
=
1
∣
Y
=
0
)
P
(
x
(
1
)
=
2
∣
Y
=
0
)
P
(
x
(
2
)
=
1
∣
Y
=
1
)
P
(
x
(
2
)
=
2
∣
Y
=
1
)
P
(
x
(
2
)
=
3
∣
Y
=
1
)
P
(
x
(
2
)
=
1
∣
Y
=
0
)
P
(
x
(
2
)
=
2
∣
Y
=
0
)
P
(
x
(
2
)
=
3
∣
Y
=
0
)
k
∑
j
=
1
n
S
j
=
2
×
(
2
+
3
)
=
10
P(x^{(1)}=1|Y=1) \\ P(x^{(1)}=2|Y=1) \\ P(x^{(1)}=1|Y=0) \\ P(x^{(1)}=2|Y=0) \\ P(x^{(2)}=1|Y=1) \\ P(x^{(2)}=2|Y=1) \\ P(x^{(2)}=3|Y=1) \\ P(x^{(2)}=1|Y=0) \\ P(x^{(2)}=2|Y=0) \\ P(x^{(2)}=3|Y=0) \\ k \sum_{j=1}^n S_j = 2 \times (2 + 3) = 10
P(x(1)=1∣Y=1)P(x(1)=2∣Y=1)P(x(1)=1∣Y=0)P(x(1)=2∣Y=0)P(x(2)=1∣Y=1)P(x(2)=2∣Y=1)P(x(2)=3∣Y=1)P(x(2)=1∣Y=0)P(x(2)=2∣Y=0)P(x(2)=3∣Y=0)kj=1∑nSj=2×(2+3)=10
因为特征数以及特征的取值数较少,因此效果不是很明显,但对比前后两个参数个数的计算公式可以发现——基于条件独立性假设可以极大地减少条件概率分布的计算量。
条件独立性假设等于是说用于分类的特征在类确定的条件下都是条件独立的。
- 优点:使朴素贝叶斯法变得简单。
- 缺点:牺牲一定的分类准确率。
在了解了条件独立性假设后,我们继续更新朴素贝叶斯公式:
P
(
y
i
∣
X
)
=
P
(
X
∣
y
i
)
P
(
y
i
)
∑
i
=
1
n
P
(
X
∣
y
i
)
P
(
y
i
)
=
∏
j
=
1
n
P
(
X
(
j
)
=
x
(
j
)
∣
y
i
)
P
(
y
i
)
∑
i
=
1
n
P
(
X
∣
y
i
)
P
(
y
i
)
P(y_i|X) = \frac{P(X|y_i)P(y_i)}{\sum_{i=1}^n P(X|y_i)P(y_i)} = \frac{\prod_{j=1}^n P(X^{(j)} = x^{(j)}|y_i)P(y_i)}{\sum_{i=1}^n P(X|y_i)P(y_i)}
P(yi∣X)=∑i=1nP(X∣yi)P(yi)P(X∣yi)P(yi)=∑i=1nP(X∣yi)P(yi)∏j=1nP(X(j)=x(j)∣yi)P(yi)
在计算过程中
P
(
X
)
=
∑
i
=
1
n
P
(
X
∣
y
i
)
P
(
y
i
)
P(X) = \sum_{i=1}^n P(X|y_i)P(y_i)
P(X)=∑i=1nP(X∣yi)P(yi) 是一个常数,并且在比较 P(y1|X) 和 P(y2|X) 时,相同项可以约去。此外,计算结果需要将后验概率最大的类输出,因此最终可得朴素贝叶斯分类器。
y
=
a
r
g
m
a
x
c
k
P
(
Y
=
c
k
)
∏
j
P
(
X
(
j
)
=
x
(
j
)
∣
Y
=
c
k
)
y = arg \ max_{c_k} P(Y=c_k)\prod_j P(X^{(j)}=x^{(j)}|Y=c_k)
y=arg maxckP(Y=ck)j∏P(X(j)=x(j)∣Y=ck)
根据上面的公式可知,朴素贝叶斯法实际上最大化后验概率,接下来就谈谈后验概率最大化的含义。
后验概率最大化的含义
朴素贝叶斯法将实例分到后验概率最大的类中,这等价于期望风险最小化。
假设选择 0-1 损失函数:
L
(
Y
,
f
(
x
)
)
=
{
1
,
Y
≠
f
(
X
)
0
,
Y
=
f
(
X
)
L(Y, f(x)) = \begin{cases} 1, \quad Y \neq f(X) \\ 0, \quad Y = f(X) \end{cases}
L(Y,f(x))={1,Y̸=f(X)0,Y=f(X)
f(X) 是分类决策函数。此时,期望风险函数为
R
e
x
p
(
f
)
=
E
[
L
(
Y
,
f
(
X
)
)
]
R_{exp}(f) = E[L(Y, f(X))]
Rexp(f)=E[L(Y,f(X))]
期望是对联合分布 P(X, Y) 取的,由此取条件期望
R
e
x
p
(
f
)
=
E
X
∑
k
=
1
K
[
L
(
c
k
,
f
(
X
)
)
]
P
(
c
k
∣
X
)
R_{exp}(f) = E_X\sum_{k=1}^K[L(c_k, f(X))]P(c_k|X)
Rexp(f)=EXk=1∑K[L(ck,f(X))]P(ck∣X)
为了使期望风险最小化,只需对 X = x 逐个极小化,由此得到:
f
(
x
)
=
a
r
g
m
i
n
y
∈
Y
∑
k
=
1
k
L
(
c
k
,
y
)
P
(
c
k
∣
X
=
x
)
=
a
r
g
m
i
n
y
∈
Y
∑
k
=
1
k
P
(
y
≠
c
k
∣
X
=
x
)
=
a
r
g
m
i
n
y
∈
Y
(
1
−
P
(
y
=
c
k
∣
X
=
x
)
=
a
r
g
m
a
x
y
∈
Y
P
(
y
=
c
k
∣
X
=
x
)
f(x) = arg \ min_{y \in Y}\sum_{k=1}^k L(c_k, y)P(c_k|X = x) \\ = arg \ min_{y \in Y}\sum_{k=1}^kP(y \neq c_k|X=x) \\ = arg \ min_{y \in Y}(1 - P(y = c_k|X=x) \\ = arg \ max_{y \in Y}P(y = c_k|X=x)
f(x)=arg miny∈Yk=1∑kL(ck,y)P(ck∣X=x)=arg miny∈Yk=1∑kP(y̸=ck∣X=x)=arg miny∈Y(1−P(y=ck∣X=x)=arg maxy∈YP(y=ck∣X=x)
这样一来,期望风险最小化准则就得到了后验概率最大化准则:
f
(
x
)
=
a
r
g
m
a
x
c
k
P
(
c
k
∣
X
=
x
)
f(x) = arg \ max_{c_k}P(c_k|X=x)
f(x)=arg maxckP(ck∣X=x)
即朴素贝叶斯法所采用的原理。
关于极大似然估计与最大后验估计可参考文章 机器学习中的MLE、MAP和贝叶斯估计。
参考
- 《统计学习方法》 李航
- 《机器学习》 周志华
- 先验概率与后验概率的区别(老迷惑了):https://blog.youkuaiyun.com/ouyang_linux007/article/details/7566339
- 机器学习中的MLE、MAP和贝叶斯估计:https://juejin.im/post/5c9c407f6fb9a071090d7606?utm_source=gold_browser_extension





















 1232
1232

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








