Java数据结构06_红黑树

介绍

  红黑树（Red Black Tree）是一种自平衡的二叉查找树，它和AVL树类似，都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能，它虽然结构复杂，但是它可在时间复杂最坏情况O(logn)内，完成查找、插入、删除操作；

约束性质

1、节点是红色或黑色；
2、根节点是黑色；
3、每个空节点（NIL节点）是黑色的；
4、每个红色节点的两个子节点都是黑色；（表明：从每个叶子到根的所有路径上不能有连个连续的红色节点）
5、从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点；
   这些约束性质强制了红黑树的关键性质：从根到任意叶子的最长可能路径不多于最短的可能路径的两倍长；

关键性质论证

  A为根节点，当A到任意叶子节点时黑色节点数为2时，那么最短可能路径为A>B,而由性质4可知，最长可能路径应为红黑相间的路径，即：A>C>E>I,红节点数==黑节点数；

红黑树的平衡操作

1、重新着色；
2、旋转：左旋、右旋；

红黑树的插入操作

• 情况1：插入的新节点N是红黑树的根节点；

• 情况2：插入新节点的父节点是黑色，满足性质4和5，不需要调整；

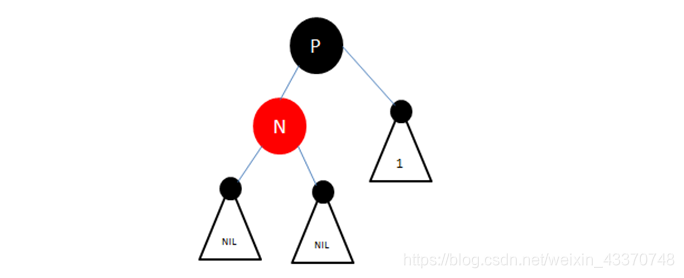
• 情况3：插入新节点N的父节点是红色（节点P为红色，其父节点必为黑色），叔叔节点U也为红色，此时性质4被破坏，这种情况下，先将P和U的颜色染为黑色，再将G的颜色染成红色，此时经过G的路径上黑色节点数量不变，性质5满足要求，但是需要注意的是G被染成红色后，可能和它的父节点形成连续的红色节点，此时需要递归向上调整；

• 情况4：N的父节点为红色，叔叔节点为黑色。节点N是P的右孩子，且节点P是G的左孩子。此时先对节点P进行左旋，调整N和P的位置。接下来按照情况5进行处理，以恢复性质4；

• 情况5：N的父节点为红色，叔叔节点为黑色。N是P的左孩子，且节点P是G的左孩子。此时对G进行右旋，调整P和G的位置，并互换颜色。经过这样的调整后，性质4被恢复，同时也未破环性质5；

红黑树的删除操作

   删除操作相对插入更为复杂，分为两步，首先进行普通二叉查找树的删除操作，然后再通过“旋转和重新着色”等一系列来修正该树，使之重新成为一棵红黑树；

红黑树的用途

   集合类TreeSet、TreeMap以及Java8以上版本的HashMap、HashSet底层都有采用了红黑树结构；