第七章 查找算法

免责声明：

• 笔记来源：本系列所有笔记均整理自 B站·王道考研·数据结构 视频教程。
• 参考书籍：《2021年数据结构考研复习指导》，王道论坛所著，电子工业出版社出版，ISBN ：9787121379819。

目录

1 查找的概念

2 线性表查找

2.1 顺序查找

顺序查找又叫做线性查找，通常用于线性表查找（顺序存储及链式存储都适用）。基本思想就是，从头到尾或者从尾到头挨个查找。

// 顺序存储结构实现线性表
typedef int E; // 线性表元素数据类型
struct SequenceList {
	E* data; // 动态数组基地址
	int length; // 顺序表长度
	int max_size; // 最大容量
};

// 初始化一个指定容量的顺序表
void Init(SequenceList& list, int init_capacity) {
	list.data = new E[init_capacity];
	list.length = 0;
	list.max_size = init_capacity;
}

// 在顺序表尾部插入一个元素
bool InsertOnTail(SequenceList& list, E e) {
	// 先判断容量是否足够
	if (list.length == list.max_size) {
		return false;
	}
	// 将元素插入尾部，从0开始存
	list.data[list.length++] = e;
	return true;
}

// 顺序查找
int SearchSeq(const SequenceList list, E e) {
	int i;
	for (i = 0; i < list.length && list.data[i] != e; i++);
	// 当i到达list.length时，说明没有查找到，返回-1
	return i == list.length ? -1 : i;
}

时间复杂度：

• 查找成功，平均查找长度ASL = (n + 1) / 2，时间复杂度为 O(n)
• 查找失败，平均查找长度ASL = n+1，时间复杂度为O(n)

2.2 二分查找

二分查找，又称为折半查找，仅适用于有序的顺序表。

算法思想：因为顺序表是有序的（假设为升序排序），先将目标值与顺序表内中间位置元素进行比较，如果相等，那么正好查找到，如果目标值较小就到顺序表的左半部分进行查找，如果目标值较大就到顺序表的右半部分进行查找；缩小查找范围、继续以通用的方式查找，从而减少比较次数，提升查找效率。

// 顺序存储结构实现线性表
typedef int E; // 线性表元素数据类型
struct SequenceList {
	E* data; // 动态数组基地址
	int length; // 顺序表长度
	int max_size; // 最大容量
};

// 初始化一个指定容量的顺序表
void Init(SequenceList& list, int init_capacity) {
	list.data = new E[init_capacity];
	list.length = 0;
	list.max_size = init_capacity;
}

// 在顺序表尾部插入一个元素
bool InsertOnTail(SequenceList& list, E e) {
	// 先判断容量是否足够
	if (list.length == list.max_size) {
		return false;
	}
	// 将元素插入尾部，从0开始存
	list.data[list.length++] = e;
	return true;
}

// 二分查找
int BinarySearch(const SequenceList list, E e) {
	int begin = 0;
	int end = list.length - 1;
	int mid;
	while (begin <= end) {
		mid = (end + begin) / 2; // 取中间位置
		if (list.data[mid] == e) {
			return mid; // 找到目标元素位置
		}
		else if (list.data[mid] > e) {
			// e 在 mid 的左边
			end = mid - 1;
		}
		else {
			// e 在 mid 的右边
			begin = mid + 1;
		}
	}
	// 至此，查找失败
	return -1;
}

时间复杂度：O(log2n)

2.3 分块查找

分块查找，又称索引顺序查找。

算法思想：将查找表分为若干个子块，子块之间是有序的，子块内部可以是无序的（第一个子块中的最大关键字小于第二个子块中所有的关键字），再使用一个索引表存储每个分块的最大关键字及对应的存储区间。查找时，现在索引表中找到目标元素应该属于哪一个分块（此时可以使用顺序查找，也可以使用二分查找，因为各分块是有序的），然后再在所属的分块内顺序查找目标元素。

3 B树和B+树

3.1 B树

B树的概念

B树的最小高度计算（B树的高度计算不包含叶子结点）：

B树最大高度计算（B树的高度计算不包含叶子结点）：

B树的插入

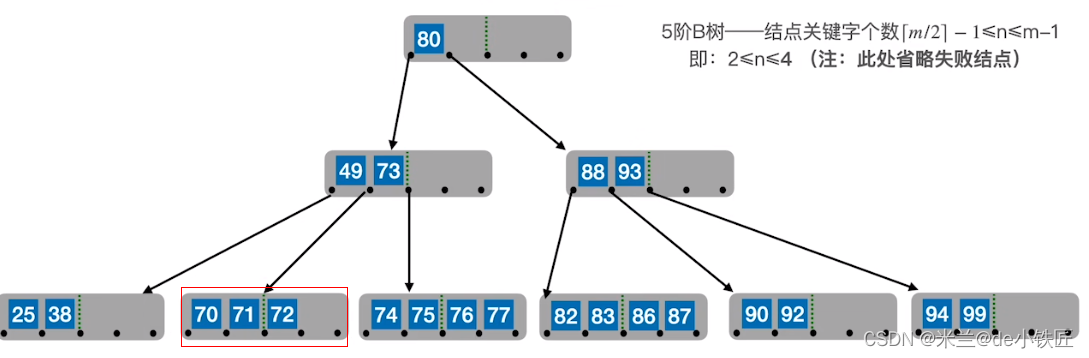
以一个5阶B树为例，结点最少有⌈m/2⌉ -1个关键字（根结点最少可以只有1个关键字），最多有 m - 1 个关键字。

例如，将序列 [25 38 49 60 80 90 99 88 83 87 70 92 93 94 73 74 75 ]各元素依次插入到一棵5阶B树中：

• 插入 25 38 49 60

• 插入 80 ，每个结点最多4个关键字，此时已经超出限制

• 从中间位置(⌈m/2⌉ = 3) 进行分裂
  
• 插入90 99，新元素一定是插入最底层的终端结点
  
• 插入 88，此时该结点超过四个关键字
  
• 从中间位置处分裂，
  
• 插入 83 87
  
• 插入70，此时该结点超过四个关键字
  
• 从中间位置处分裂
  
• 插入92 93 94 ，此时该结点关键字超过四个
  
• 从中间位置分裂
  
• 插入73 74 75，结点关键字超过4个
  
• 从中间位置分裂
  
• 此时，父结点的关键字也超出了限制，以同样的方式分裂
  

B树的删除

• 删除的关键字在终端结点，可以直接删除，但是要注意，删除后结点所剩关键字个数不能低于下限⌈m/2⌉ -1 = 2。假如删除 60，该关键字处于终端结点，且删除后，所处结点的剩余关键字为3，满足非叶子结点最少应该有⌈m/2⌉ -1 = 2个关键字的要求，可以直接删除 60
  
• 删除关键字在非终端结点，可以将其转换为对终端结点上关键字的删除操作。方式一：使用直接前驱（左侧指针所指子树中最右下的元素）来替换待删除关键字；方式二：使用直接后继（右侧指针所指子树中最左下的元素）来替换待删除关键字。例如，删除80，使用其直接前驱77替换80，转换成在终端结点上删除77
  
  
  比如，删除77，使用其直接后继 82替换，转换成在终端结点删除82
  
  
• 对终端结点关键字删除时，如果剩余关键字低于下限，如果兄弟结点剩余关键字足够，就要从兄弟结点借一个关键字来补上。方式一：给右边的兄弟借，比如删除38，删除后，所处结点的关键字只剩下25，个数少于2，此时右边的结点还有3个关键字，可以借一个，具体做法是，找到25 的后继的后继（即70），用70顶替25的后继（即49），然后将49补到38的位置，这样就保证了B数的特性
  
  方式二，给左边的兄弟借，比如删除92，删除后，所处结点的关键字只剩下90，个数少于2，此时左边的结点还有3个关键字，可以借一个，具体做法是，找到90的前驱的前驱（即87），使用87顶替90的前驱（即88），然后将88补到92的位置
  
• 对终端结点关键字删除时，如果剩余关键字低于下限，且兄弟结点剩余关键字不够借时，就要将删除关键字后的结点与其左（或右）兄弟结点及他们的父结点中对应的关键字进行合并，比如，删除 49，此时其右兄弟只有两个关键字，不够借，就要将当前结点剩下的25和右边的结点中的71，72以及他们的父结点中对应的关键字 70 进行合并
  
  但是，由于合并导致他们的父结点关键字低于2，且其父结点的右边的结点也不够借，继续以同样的方式合并，将 73 与 87,93及根结点中的82合并
  

3.2 B+树

B树与B+树对比

区别1：

• M阶B+树：结点中n个关键字对应n棵子树
• M阶B树：结点中n个关键字对应n+1棵子树

区别2：

• M阶B+树：根结点中关键字个数范围[1 , m]；其他结点关键字个数范围[⌈m/2⌉ , m]
• M阶B树：根结点中关键字个数范围[1 , m - 1]；其他结点关键字个数范围[⌈m/2⌉ - 1 , m - 1]

区别3：

• M阶B+树：叶子结点包含全部关键字（非叶子结点中出现过的关键字都会包含在叶子结点中）
• M阶B树：叶子结点和非叶子结点中的关键字都不一样

区别4：

• M阶B+树中，所有的非叶子结点仅仅起到索引作用，其中的每个索引项只包含对应子树的最大关键字和指向该子树的指针，不包含该关键字对应记录的存储地址
• M阶B树中，每个结点既包含了关键字信息，也包含了对应记录的存储地址（如果需要的话）

区别5：

• M阶B+树对比B树，因为非叶子结点不含有该关键字对应的记录的存储地址信息，可以使得一个磁盘块（一般存储一个结点）能够包含更多关键字，使得B+树的阶更大（树更宽），从而使得树更矮，读取磁盘次数更少，查找更快。例如，MySQL的索引系统就是通过B+树来实现的。

4 散列查找

4.1 散列表的概念

• 散列（哈希）函数：将关键字映射成关键字对应的地址的函数（地址可以是数组下标、索引或者内存地址）。
• 同义词：不同的关键字，通过同一散列函数映射到同一个地址，称它们为同义词。
• 冲突：通过散列函数确定的位置上一级存放了其他的元素，这种情况叫做冲突。冲突只能通过优化散列函数来尽量减少，但是终究是不可避免，所以还要设计出较好的处理冲突的方法。
• 散列（哈希）表：通过散列函数建立一种关键字与存储地址直接映射关系，是一种根据关键字直接访问的数据结构。理想情况下，散列表的查找时间复杂度应该为O(1)，即与散列表中元素数量无关。

4.2 常见的散列函数

除留余数法

为什么一定要取质数？

可以看出，散列表长度为8 ，哈希函数取 H(key) = key % 8 碰撞还没有 取 H(key) = key % 7 的严重，这是因为关键字是连续的自然数。更换一批关键字测试：

可以看出，利用质数来取模能够让关键字分布的更加均匀（通过数论相关知识来论证）。

直接定址法

数字分析法

平方取中法

4.3 哈希冲突

拉链法

查找成功：

查找失败：

查找成功的平均查找长度：

最理想的情况下，查找时间复杂度应该是O(1)。为了减少冲突，提高查找效率，就要设计出更加优秀的哈希函数。

开放定址法

其中的重点是如何确定增量序列 di，有三种方法：

• 线性探测法：发生冲突时，每次往后探测相邻的下一个位置是否为空，如果为空就存入，不为空则继续往后探测。

  • 插入元素1，H(1) = 1 % 13 = 1；第0次冲突 H0 = (H(1) + 0) % 16 = 1，发生冲突，第1次冲突H1 = (H(1) + 1) % 16 = 2，因此将元素1存入索引为2的位置
  • 插入元素68，H(68) = 68 % 13= 3，将元素68存入索引为3的位置
  • 插入元素20，H(20) = 20 % 13 = 7，将元素20存入索引为7的位置
  • 插入元素84，H(84) = 84 % 13 = 6，第0次冲突 H0 = (H(84) + 0) % 16 = 6，发生冲突，第1次冲突H1 = (H(84) + 1) % 16 = 7，发生冲突，第2次冲突H2 = (H(84) + 2) % 16 = 8，因此将元素84存入索引为8的位置
    
    

• 平方探测法:

注意：使用平方探测法的时候，散列表的长度必须是一个可以表示为4*j+3的质数，才能探测到所有的位置。

• 伪随机序列法：di 是某个伪随机序列

再散列法