算法复杂度:
分为时间复杂度和空间复杂度。 其作用: 时间复杂度是指执行算法所需要的计算工作量;而空间复杂度是指执行这个算法所需要的内存空间。
稳定性:
在一个待排序的序列中,存在2个相等的数,在排序后这两个数的相对位置保持不变,那么该排序算法是稳定的,否则是不稳定的。
直接插入排序
排序思想:
通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入,如此重复,直至完成序列排序。
时间复杂度:
最好情况下:O(n) 最坏情况下:O(n^2)
空间复杂度: O(1)
稳定性: 稳定
优点: 越有序越快
缺点: 比较的次数不一定,比较次数越少,插入点的数据移动就越多,特别是数据较多时。
核心代码解析
public static void insertSort(int[] array) {//插入排序
int tmp = 0;
for (int i = 1; i < array.length; i++) {
tmp = array[i];//将i号下标的值赋给tmp
int j = 0;
for (j = i-1; j >= 0; j--) {
if(array[j] > tmp) {//当tmp的值小于j号下标的值时
array[j+1] = array[j];//将j号下标的值赋给j+1
} else {//当tmp的值大于j号下标的值时
break;//跳出本循环
}
}
array[j+1] = tmp;//把tmp的值j号下标的值赋给j+1
}
}
画图详解
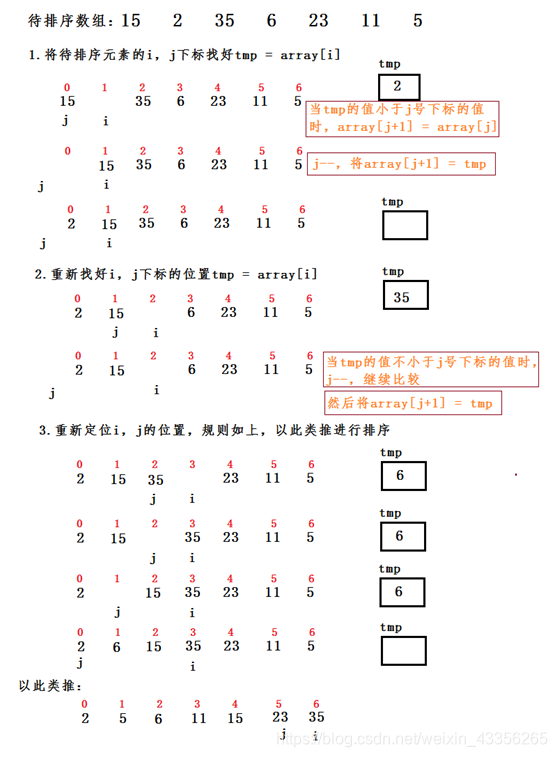
直接选择排序
排序思想:
每i趟中都找到所有元素中最小的元素,放置到i号下标处(已排序好的,不参与查找),如此重复,直至完成序列排序。
时间复杂度:
最好情况下:O(n^2) 最坏情况下:O(n^2)
空间复杂度: O(1)
稳定性: 不稳定
优点: 移动数据的次数已知是(n-1次)
缺点: 比较次数多
核心代码解析
public static void selectSort(int[] array) {//选择排序
int tmp = 0;
for (int i = 0; i < array.length; i++) {
for (int j = i+1; j < array.length; j++) {
if(array[j] < array[i]) {//如果j号下标的值小于i号下标的值
tmp = array[i];//i、j号下标的值进行交换
array[i] = array[j];//保证i号下标的值永远<=j号下标的值
array[j] =tmp;
}
}
}
}
画图详解
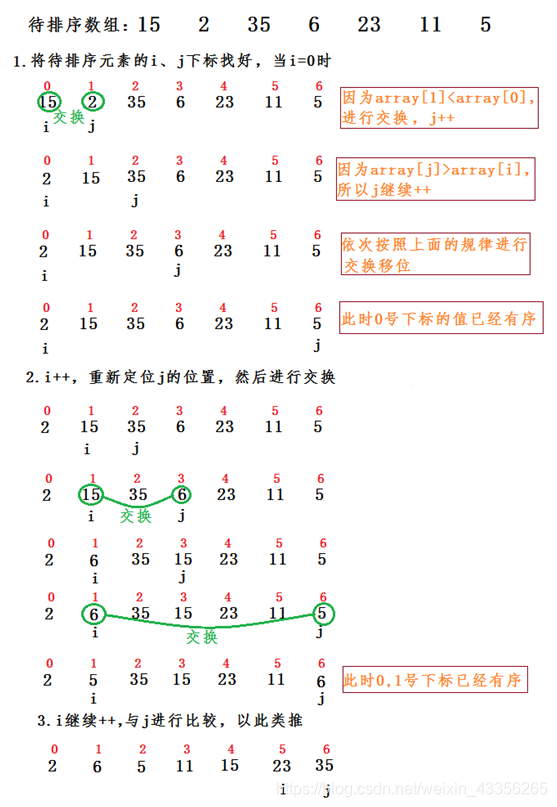
冒泡排序
排序思想:
两两比较待排序记录的元素,发现两个记录的次序相反时即进行交换,直至没有反序为止。
时间复杂度:
最好情况下:O(n) 最坏情况下:O(n^2)
空间复杂度: O(1)
稳定性: 稳定
缺点: 比较慢,每次只能移动相邻的两个数据
核心代码解析
public static void bubbleSort(int[] array) {//5 4
boolean swap = false;//冒泡的优化,定义起初没有被交换,即无序
for (int i = 0; i < array.length-1; i++) {//趟数
for (int j = 0; j < array.length-1-i; j++) {//比较
if(array[j] > array[j+1]) {//当j号下标的值大于j+1号下标值时
int tmp = array[j];//进行交换
array[j] = array[j+1];
array[j+1] = tmp;
swap = true;//交换过后,有序
}
}
if(!swap) {//如果是有序,直接return
return;
}
}
}
画图详解

冒泡排序和选择排序的具体分析区别
1、冒泡排序具体详解:
就像它的名字一样,小的在上(前),大的在下(后),比较相邻的两个数,依次先寻找大的。(将大的沉底)
第一趟:首先比较第1个和第2个数,将小数放前,大数放后。然后比较第2个数和第3个数,将小数放前,大数放后,如此继续,直至比较最后两个数,将小数放前,大数放后。至此第一趟结束,将最大的数放到了最后。
第二趟:仍从第一对数开始比较 (因为可能由于第2个数和第3个数的交换,使得第1个数不再小于第2个 数),将小数放前中,大数放后,一直比较到倒数第二个数(倒数第一的位置上已经是最大的),第二趟 结束,在倒数第二的位置上得到一个新的最大数(其实在整个数列中是第二大的数)。
如此下去,重复以上过程,直至最终完成排序。
2、选择排序具体详解:
第一次从下标为0的开始下标为0的这个数与后面的n-1个进行比较;找出最小或者最大的放在下标为0的这个位置;第二次从下标为1的开始比较;查询剩下的最大或者最小值;放在 下标为1的位置;以此类推;直到排序完成(是对冒泡排序的一种改进)
shell排序
排序思想:
(分组的思想)不断把待排序的对象分成若干小组,对同一小组内的对象采用直接插入排序,当完成了所有对象都在一个组内的排序后,排序结束
时间复杂度:
最好情况下:O(n) 最坏情况下:O(n^2)
空间复杂度: O(1)
稳定性: 不稳定
优点: 快,数据移动少
核心代码解析
public static void shell(int[] array,int gap) {//定义一个数组和分组的大小
int tmp = 0;
for (int i = gap; i < array.length; i++) {//组的大小要小于数组长度
tmp = array[i];//将组内i号下标的值赋给tmp
int j = 0;
for (j = i-gap; j >= 0; j -= gap) {//j的位置,j的步径
if(array[j] > tmp) {//当j号下标的值大于tmp时
array[j+gap] = array[j];//在组内交换
} else {
break;
}
}
array[j+gap] = tmp;//将tmp的值赋给(j+gap)号下标
}
}
public static void shellSort(int[] array) {//shell 排序
int drr[] = {7,5,3,1};//分的组数
for (int i = 0; i < drr.length; i++) {//分的组数依次减小的循环
shell(array,drr[i]);//调用shell小组的排序
}
}
画图详解
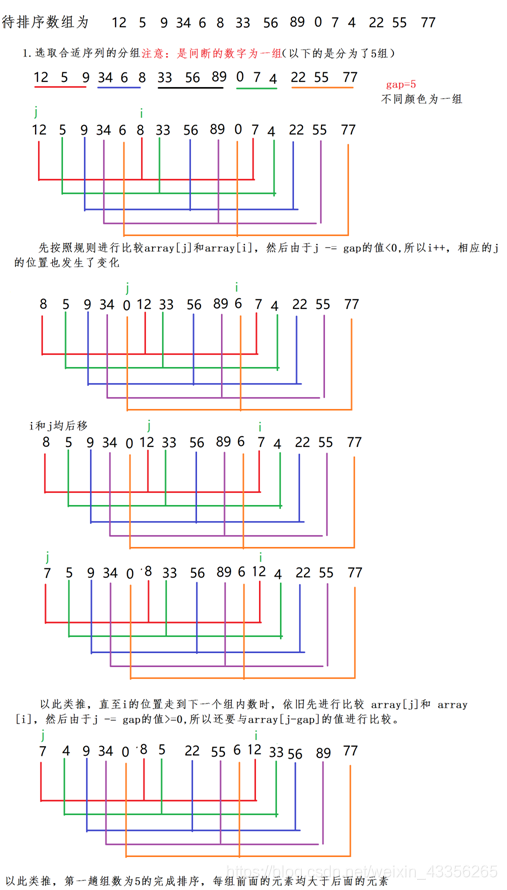
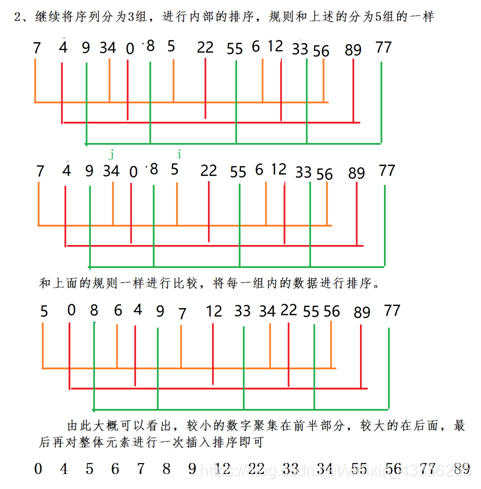








 本文深入讲解了五种经典的排序算法:直接插入排序、直接选择排序、冒泡排序、Shell排序和快速排序。详细分析了每种算法的时间复杂度、空间复杂度及稳定性,并提供了核心代码解析,帮助读者理解算法原理。
本文深入讲解了五种经典的排序算法:直接插入排序、直接选择排序、冒泡排序、Shell排序和快速排序。详细分析了每种算法的时间复杂度、空间复杂度及稳定性,并提供了核心代码解析,帮助读者理解算法原理。
















 972
972

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








