五 （未做：137，）. LeetCode标签刷题——位运算 算法部分

位运算:
最常用的两种操作：

求n的二进制表示中第k位（最低位从0开始）数字是几: (n >> k )& 1：即n右移k位再与1相与。
返回n的二进制最后一位1(或者说最高位1）：lowbit(n) = (n & -n)  即：n与-n相与。

左移右移，&，^都是针对二进制数字。

如：

n=1000000001100000

最后一位1是加粗那个1。

首先先掌握下常规二进制的操作把
基本操作
a = 0 ^ a = a ^ 0
0 = a^a
由上面两个推导出：a = a ^ b ^ b
交换两个数
a = a^b
b = a^b
a = a^b
移除最后一个 1
a = n&(n-1)
获取最后一个 1
diff = (n&(n-1))^n

题目描述 给定一个长度为n的数列，请你求出数列中每个数的二进制表示中1的个数。

输入格式 第一行包含整数n。

第二行包含n个整数，表示整个数列。

输出格式 共一行，包含n个整数，其中的第 i 个数表示数列中的第 i 个数的二进制表示中1的个数。

数据范围 1≤n≤100000, 0≤数列中元素的值≤109

代码：

#include <iostream>
 using namespace std;
 
 //实现lowbit操作
 int lowbit(int x){
     return x&-x;
 }
 int main(){
     int n;
     cin>>n;
     while(n--){
         int x;
         cin>>x;
         int res=0;  //res记录每一个x的二进制中1的个数；
         while(x){
             x-=lowbit(x);  //每次减去x的最后一位1，
             res++; //没减一次1的个数加上1.
         }
     }
 }

29. 两数相除（快速幂+二进制）

给定两个整数，被除数 dividend 和除数 divisor。将两数相除，要求不使用乘法、除法和 mod 运算符。

返回被除数 dividend 除以除数 divisor 得到的商。

整数除法的结果应当截去（truncate）其小数部分，
例如：truncate(8.345) = 8 以及 truncate(-2.7335) = -2

示例 1:

输入: dividend = 10, divisor = 3
输出: 3
解释: 10/3 = truncate(3.33333..) = truncate(3) = 3

示例 2:

输入: dividend = 7, divisor = -3
输出: -2
解释: 7/-3 = truncate(-2.33333..) = -2
 

> 提示：
> 
> 被除数和除数均为 32 位有符号整数。 除数不为 0。
> 假设我们的环境只能存储 32 位有符号整数，其数值范围是 [−2^31,  2^31 − 1]。
> 本题中，如果除法结果溢出，则返回 2^31 − 1。

算法分析：
快速幂+二进制，位运算

算法思路
该题目要求返回两个数相除下取整的结果，但是要求不使用乘法、除法和 mod 运算符。都知道乘法是求相同的几个数相加，那么反过来除法就是求被除数里面最多有几个除数。因此一个直观的想法就是利用减法，每次减去除数，直到被除数减为零或减到小于除数时，减去的除数个数即为相除结果。

但是该方法如果在被除数很大，而除数很小时，时间复杂度会非常高，以此题为例，题目中被除数和除数范围均在[−2³¹,2³¹−1]中，当被除数取最大，除数为1时，结果会约等于231231,如果选择每次减1，则最终时间复杂度会达到上亿级，因此我们需要对算法进行优化。

• 1、先考虑相除后是正数的情况，x/y=t，因此 x=ty+余数，将b,2b,4b,8b,....2nb的所有小于a的数值存在exp链表中，且exp链表元素大小从小到大排列
• 2、从exp末端开始枚举，若a >= exp.get(i)，则表示 t 包含1 << i这个数值，将 2^i加入到res中，并且更新a，a -= exp.get(i)
  

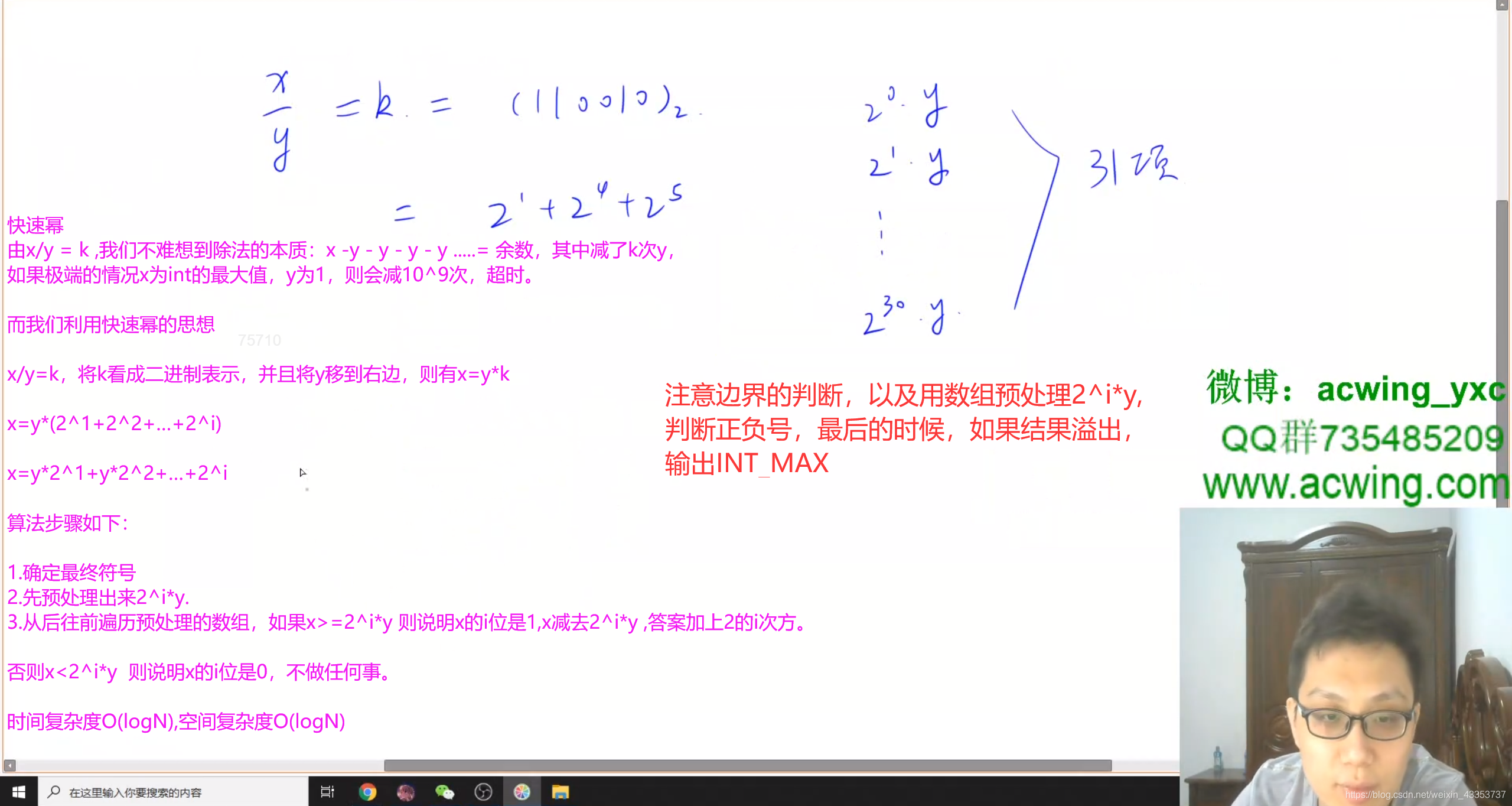
符号和数值分开计算 注意2个地方的溢出res += 1LL << i; 和 res > INT_MAX || res < INT_MIN

代码：

class Solution {
public:
    int divide(int x, int y) {
        typedef long long ll;   //下面方便一点
        vector<ll> exp; //指数项数组，下面我们需要预处理出来指数项数组，
        bool is=false;  //记录结果是否是负号，初始化为false,即不是负号
        if((x<0&&y>0)||(x>0&&y<0)) is=true; //即结果是负号把is改为true
        //先都直接用正数算，到时候结果加上负号就可以
        ll a=abs((ll)x),b=abs((ll)y);   //注意这里x,y之前一定要加long long ,否则如果x或者y是-2^31则变为绝对值会溢出
        //下面预处理指数项数组//即预处理2*b^i,存的就是2^0*y,2^1*y,......一直到最大的一个值乘以y
        //预处理y*(2的i次方)// 将分子对应的比特位存下来, 不需要存31位,只需将小于分母的所有比特位保存下来就行v
        for(ll i=b;i<=a;i=i+i) exp.push_back(i);//i从除数b开始，只要i还小于被除数a，就倍增i，然后将指数项插入到exp数组里,注意不是i++,而是i=i+i。
        //下面就需要从大到小枚举一下图片中的过程
        ll res=0;   //res存储答案
        //逆序遍历分子比特位, 如果被减数>=减数那么说明商的这一位是1, 对应比特位由1<<i位得到
        for(int i=exp.size()-1;i>=0;i--){ //从最高位(n-1)到最低位(0)开始减
            if(a>=exp[i]){  //x大于exp[i],即还可以做减法
                a-=exp[i];  //就从被减数中减去对应的数
                //够减，就让结果加上2^i（即1左移i位），注意不是加上exp[i],因为exp[i]中存放的是商乘以除数，而我们这里只能加上商。
                res+=(ll)1<<i;  //左移一位，相当于乘以2，因为是基于倍增的思想，所以能减多少次，就左移多少次即可得到结果,并且注意这里最多可能移31位,这样的话就会溢出，所以这里加上ll,且是加在i前面，不是（i<<i）的前面
            }
        }
        //负号的话就直接取反
        if(is==true) res=-res;  //如果答案是负数，res更新为负的res
        //处理溢出的情况// 判断有没有超出int范围
        if(res>INT_MAX||res<INT_MIN) res=INT_MAX;   //如果结果正溢出或者负溢出，res更新为INT_MAX(题目中规定的)
        return res; //注意到最后更新res之后（可能会更新也可能不会）再输出res
    }
};

java代码：

class Solution {
    public int divide(int a, int b) {
        List<Long> e=new ArrayList<>();
        long x=Math.abs((long)a),y=Math.abs((long)b);
        for(long i=y;i<=x;i=i+i) e.add(i);
        long res=0L;
        for(int i=e.size()-1;i>=0;i--){
            if(x>=e.get(i)){
                x-=e.get(i);
                res+=(long)1<<i;
            }
        }
        if((a>0&&b<0)||(a<0&&b>0)) res=-res;
        if(res>Integer.MAX_VALUE||res<Integer.MIN_VALUE) res=Integer.MAX_VALUE;
        return (int)res;
    }
}

2021年9月19日17:59:51：

class Solution {
    public int divide(int x, int y) {
        if(y==1) return x;
        if(x==Integer.MIN_VALUE&&y==-1) return Integer.MAX_VALUE; //溢出的情况特判掉
        int minus=1; //minus存储结果的符号，1表示结果为正，-1表示为负
        if((x>0&&y<0)||(x<0&&y>0)) minus=-1; //结果是负数，我们就将mihus设置为-1

        List<Long> e=new ArrayList<>(); //e数组记录图上的所有的2^n*y项
        long a=Math.abs((long)x),b=Math.abs((long)y); //处理完符号，我们就要将x,y都取其绝对值，转为正数除以正数的情况,注意一定要先将x,y转为long,再求其绝对值
        for(long i=b;i<=a;i=i+i) { //i最小是2^0*y,即b,最大不超过a, 
            e.add(i); //经过这一步操作就可以把2^0*y,2^1*y,...,2^30*y都放到e数组中了，i=i+i即i=2*i,而i初始化为b,即每次循环都让b乘以一个2
        }  
        //注意这里i<=a就停止了，即可能不会到2^30*y,只能直到2^10*y就停止计算了，
        long k=0L; //k是答案
        //再从大到小即e数组的最后一个数一直到e数组的第一个数，求一下商
        for(int i=e.size()-1;i>=0;i--){ //注意e数组中存储的就是2^0*y,2^1*y,...,2^n*y,我们从e数组的最后一位开始往前看
            if(a>=e.get(i)){  //当x比这个数大的时候，就让x减去这个数，并让k加上2^i，2的i次方即1左移i位，注意是a,因为我们这里用的是正的x即a，注意是>=，=的时候也要减去，=也够用了
                a-=e.get(i); //先让x减去这个数字即e[i]
                k+=(long)1<<i; //再让答案加上2^i次方，注意1左移,最多移位31位，结果会溢出，这里的一位操作也要用long
            }
        }
        k*=minus; //结果k要乘以对应的符号
        if(k>Integer.MAX_VALUE||k<Integer.MIN_VALUE) return Integer.MAX_VALUE;
        return (int)k;
    }
}

2021年11月10日11:49:36：

class Solution {

//不让我们使用乘除法,所以我们只能使用加减,而如果我们直接暴力减的话,当x特别大(2^31-1),而y特别小(1)的时候,就会超时,所以我们考虑使用快速幂优化
//假设x/y=k,也就是说x最多能被减k次y,我们现在不一个一个y的减,而是使用二进制的方式,比如k的二进制表示是(110010),即k=2^1+2^4+2^5,
//本来x-k*y=0,现在就变成了x-2^1*y-2^4^y-2^5*y,由于一个数在被二进制表示之后最多只有logn位(以2为底),也就是说x最多减31次,
//x最大是2^31-1,所以最大我们只需要预处理出来2^30*y
//所以我们可以先预处理出来2^0*y,2^1*y,...,2^30*y的值,之后再从2^30*y开始看,如果x>=2^30*y,则说明x/y>=2^30,则说明k中有2^30这一项,即k要加上2^30
//而如果有一项是负数的话,我们先存负号,最后用两个数的绝对值去除即可

    public int divide(int x, int y) {
        List<Long> st=new ArrayList<>();  //数组st存储我们预处理的2^?*y,?从0到30,结果可能溢出,所以需要用long来存储
        int is=1; //先判断结果的符号,is存储结果的符号,1代表是正号，-1代表是符号
        if((x>0&&y<0)||(x<0&&y>0)) is=-1; //x,y中有一个是负数,is就是true表示结果是负数
        long a=Math.abs((long)x),b=Math.abs((long)y); //先对x,y取绝对值再进行运算,注意a,b中可能是有-2^31的,如果取绝对值就会溢出,所以我们要用long来存储
        //之后要预处理出来2^? * y
        for(long k=b;k<=a;k=k*2){ //最小是2^0*b即是b,最大不能超过a,每次要乘以2，注意这里不能用乘法，所以k=k*2应该改为k=k+k=k*2
            st.add(k); //加到数组中
        }
        //之后再从高位往低位判断
        long res=0; //结果可能溢出所以这里要用long来存储答案
        int n=st.size();
        for(int i=n-1;i>=0;i--){  //从最高位开始看，即从大到小求商
            if(a>=st.get(i)) {  //如果a>=2^? *y,就说明组成商的这一位上是1
                a-=st.get(i);
                res+=(1L<<i);  //res要加上1<<i,而左移可能溢出，所以要使用long类型
            }
        }
        res*=is;  //最后res要乘以符号
        if(res>Integer.MAX_VALUE||res<Integer.MIN_VALUE) return Integer.MAX_VALUE;  //结果是溢出，就返回正无穷大
        return (int)res; //没有溢出就返回正常的结果
    }
}

50. Pow(x, n) （快速幂，二进制, 和29题很像）

实现 pow(x, n) ，即计算 x 的 n 次幂函数（即，x^n）。

示例 1：

输入：x = 2.00000, n = 10
输出：1024.00000

示例 2：

输入：x = 2.10000, n = 3
输出：9.26100

示例 3：

输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25

提示：

-100.0 < x < 100.0
-231 <= n <= 231-1
-104 <= xn <= 104

class Solution {
public:
    double myPow(double x, int n) {
        typedef long long LL;
        bool is_minus=(n<0);   //定义一个bool值is_minus,判断其是否小于0，如果为负数<0, 则is_minus为true; 如果为正数>0,则is_minus为false。
        double res=1;   //定义答案结果。
        for(LL k=abs(n);k;k>>=1){  //先把n取绝对值转为正值k，if语句即枚举k（n）的二进制中的每一位（个位->十位->百位->......），如果这一位上数值不为零，且x最开始就等于x的2^0;
            if(k&1) res*=x; //如果k的这一位的二进制不为零，答案里面就要乘上x对应的次幂，
            x*=x;   //并且每一次循环我们都要记录下来x对应的次幂，这一步是乘以上一次的x,即x*x=x^2。以便下次如果对应位上的数值不为零，我们要乘上x对应的次幂。
        }
        if(is_minus) res=1/res;     //如果is_minus为负数<0,则res=1/res;
        return res; //最后返回结果。
    }
};

2021年9月20日12:27:00：

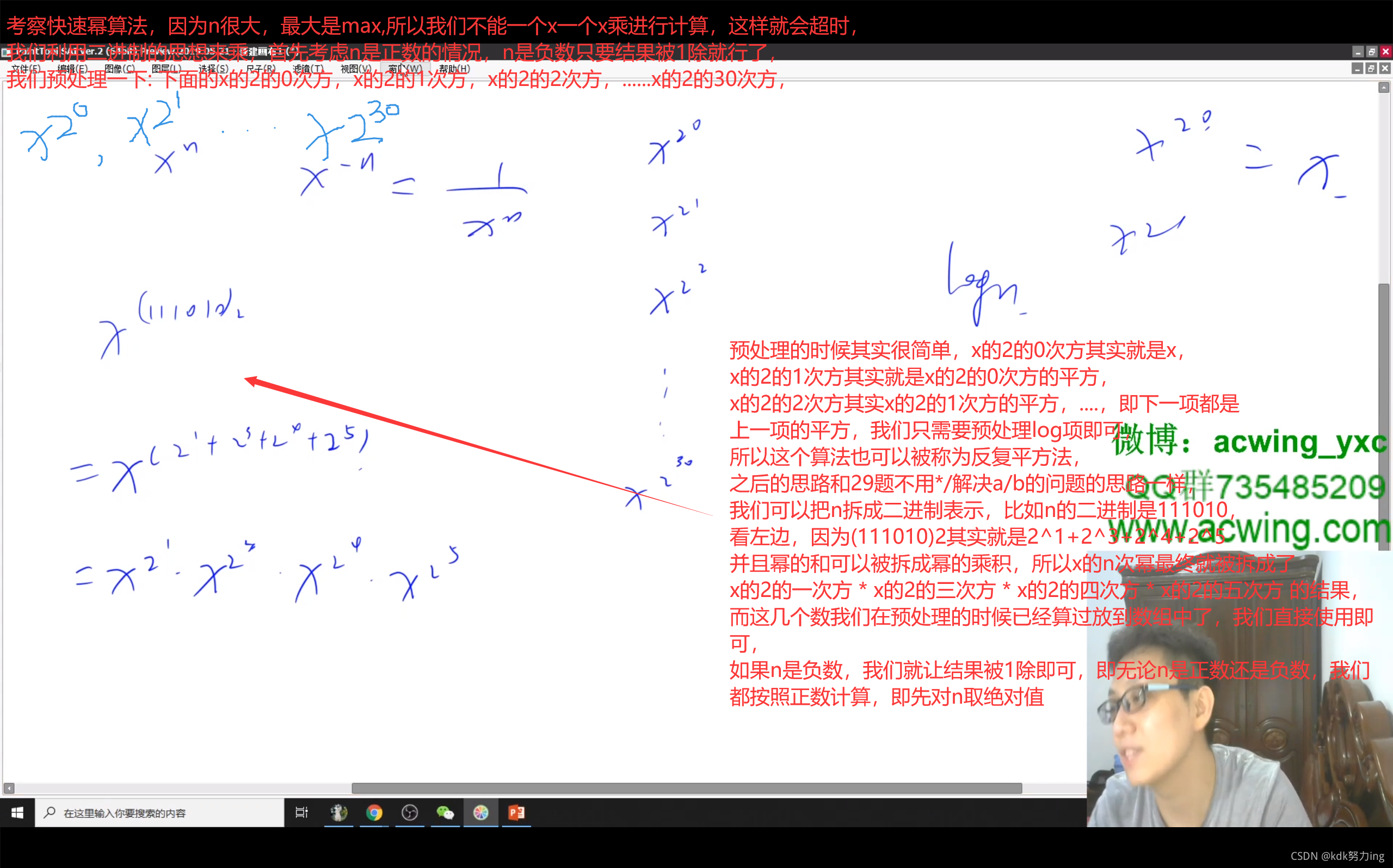
//考察快速幂算法，因为n很大，最大是max,所以我们不能一个x一个x乘进行计算，这样就会超时，我们利用二进制的思想来乘，
//注意x的2的n次幂数组我们可以不用预处理，我们可以在计算答案的过程中，边计算边预处理这个数组,这一点很巧妙
class Solution {
    public double myPow(double x, int _n) {
        int minus=1; //minus记录n的符号
        if(_n<0) minus=-1; //n是负数的话，结果要取倒数，我们先记录一下n的符号
        //下面将n取绝对值，因为n最小是min, 如果取绝对值的话会溢出，所以我们要将int转为long,即使用long型
        long n=Math.abs((long)_n); //先将_n取绝对值,因为一个变量不能被定义两次，我们要用一共新的变量定义，或者将给的n改一下
        //边计算答案边预处理数组
        double res=1.0; //res是答案
        for(;n>0;n>>=1){ //只要n还大于0，我们就需要取出n的二进制的每一位(从二进制的个位开始取，每次左移一位，即依次取到n的二进制表示的个位，十位，...)
            if((n&1) !=0) res*=x; //如果这一位不为0，即我们要在答案上乘以其对应的次幂，比如样例中的res=x的2^1+x的2^3+x的2^4,
            //之后还要更新x的2^?的平方的值
            x*=x; //算这个数的平方(此时x就是这个数的平方)就是这个数再乘以这个数本身一次就可以了 
        }
        if(minus<0) res=1/res; //如果是算的负次幂，就将结果取倒数
        return res;
    }
}

78. 子集

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

 示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]
 

提示：
1 <= nums.length <= 10
-10 <= nums[i] <= 10
nums 中的所有元素 互不相同

用二进制的方法

由于每个数有选和不选两种情况，因此总共有 2^n 种情况，用二进制 0 到 2^n-1 表示所有的情况（如3个数的集合就用000~111表示），在某种情况i中，若该二进制i的第j位是1，则表示第j位这个数选，加入到path中，枚举完i这种情况，将path加入到ans答案数组中。

代码：

class Solution {
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        vector<vector<int>> res;    //记录答案。
        int n=nums.size();  //n记录数组长度。
        for(int i=0;i< 1<<n;i++){   //枚举从0到2^n-1，共2^n个子集，注意这里是1<<n,不是2<<n。
            vector<int> path;   //记录这一次的答案
            for(int j=0;j<n;j++){   //枚举二进制每一位是0还是1（如图片样例n=3,）
                if(i>>j&1){    //看一下i的第j位是0还是1，如果第j为是1的话，我们就把这个数（nums[j]）加到方案数组中，注意这里是（i>>j&1）。
                    path.push_back(nums[j]);
                }
            }
            //每结束一次for循环，我们就得到了一个子集，就把这个子集加到方案里。
            res.push_back(path);
        }
        return res;    //最后记得将答案返回。
    }
};

136. 只出现一次的数字

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

说明：
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？

示例 1:

输入: [2,2,1]
输出: 1

示例 2:

输入: [4,1,2,1,2]
输出: 4

算法分析：
位运算，异或操作。

异或运算具有交换律，结合律（加法具有的性质异或运算均有），同零异一。

0异或任何数结果均是其本身，所以我们初始化res为0，不是1。一定要注意。

算法
(位运算) O(n)

1. 两个相同的数字经过异或之后会变为 0。
2. 将数组所有元素异或在一起即可得到出现 1 次的元素值。
   时间复杂度

• 仅遍历一次数组，故时间复杂度为 O(n)。
  空间复杂度
• 仅需要常数的额外空间。
  
  即我们在理解的时候把两个相同的数放在一起异或，结果是0,0异或任何数结果都是其本身。

思路
1.0与任何数异或都为原数：0 ^ n = n;
2.自己与自己异或为0 ：n ^ n = 0 ;
3.异或具有交换律 ： a ^ b ^ c = a ^ c ^ b

所以这个题目我们直接使用交换律：a ^ b ^ c ^ d ^ a ^ b ^ c =a ^ a ^ b ^ b ^ c ^ c ^ d=d(d就是那个只出现一次的数）

代码：

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int res=0;
        for(auto x:nums){
            res^=x;
        }
        return res;
    }
};

算法二：哈希表
若第一次出现，插入哈希集
第二次出现，冲哈希集内删除
最后剩下的就是那个只出现一次的数字

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        unordered_set<int> bobo;
        int ans;
        for(auto i : nums){
            if(bobo.count(i))   bobo.erase(i);
            else    bobo.insert(i);
        }
        for(auto j : bobo)  ans = j;
        return ans;
    }
};

2021年8月28日12:54:34：

思路：数组中有一个数只出现了一次，其他数都出现了两次，可以利用异或法，因为两个相同的数异或等于0，两两消去，剩下的就是那个只出现了一次的数。

位运算之异或运算的规律：

1. 交换律：a ^ b ^ c <=> a ^ c ^ b

2. 任何数与0异或为任何数 0 ^ n = n

3. 相同的数异或为0: n ^ n => 0

var a = [2,3,2,4,4]

2 ^ 3 ^ 2 ^ 4 ^ 4等价于 2 ^ 2 ^ 4 ^ 4 ^ 3 => 0 ^ 0 ^3 => 3

class Solution {
    public int singleNumber(int[] nums) {
        int res=0;  //注意res要初始化为0，因为最后剩下的的那个单独的数由于“同零异一”，所以必须是全零最后得到的才是那个独一无二的数
        for(int x:nums) res^=x;
        return res;
    }
}

137. 只出现一次的数字 II

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现了三次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？

示例 1:

输入: [2,2,3,2]
输出: 3

示例 2:

输入: [0,1,0,1,0,1,99]
输出: 99

算法一：
算法分析：
位运算：状态机

LeetCode上金木盐的解析：

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int a = 0, b = 0;
        for (auto num : nums)
        {
            a = (a ^ num) & ~b;
            b = (b ^ num) & ~a;
        }
        return a;
    }
};

解释下：假设有一个数为x,那么则有如下规律：

• 0 ^ x = x,

• x ^ x = 0；

• x & ~x = 0,

• x & ~0 =x;

那么就是很好解释上面的代码了。一开始a = 0, b = 0;

1. x第一次出现后，a = (a ^ x) & ~b的结果为 a = x, b = (b ^ x) & ~a的结果为此时因为a = x了，所以b = 0。

2. x第二次出现：a = (a ^ x) & ~b, a = (x ^ x) & ~0, a = 0; b = (b ^ x) & ~a 化简，

b = (0 ^ x) & ~0 ,b = x;

3. x第三次出现：a = (a ^ x) & ~b， a = (0 ^ x) & ~x ,a = 0; b = (b ^ x) & ~a 化简， b = (x ^ x) & ~0 , b = 0;所以出现三次同一个数，a和b最终都变回了0.

4. 只出现一次的数，按照上面x第一次出现的规律可知a = x, b = 0;因此最后返回在这里插入代码片a.
   
   代码：

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int two=0,one=0;    //用00表示余0这种状态，01表示余1这种状态，10表示余2这种状态
        for(auto x:nums){   //取出数组中所有数
            one=(one^x)&(~two); //更新one
            two=(two^x)&(~one); //更新two
        }
        return one; //最后返回one
    }
};

疑惑点：为啥return one 还是不太清楚。 two=0， one=1表示的是 1这个状态，也就是余数为1的状态，但是为啥返回值是 one就可以了呢？不太理解。

答：
每一位是独立的，每一位里我们希望统计的是1出现的次数是否模3余1，如果1的次数模3余0，那么one、two都是0，如果余1，那么one=1，two=0，如果余2，那么one=0，two=1。所以如果one=1，那这一位就应该是1，如果one=0，那这一位就应该是0。所以最后返回one就可以了。

算法二：
(位运算) O(n)

1. 根据 Single Number 的做法，可以推广到更一般的问题。
2. 考虑二进制每一位上出现 0 和 1 的次数，如果出现 1 的次数为 3k + 1，则证明答案中这一位是 1。
   时间复杂度：
   仅遍历 32 次数组，故时间复杂度为 O(n)。
   空间复杂度：
   仅需要常数的额外空间。

代码：
class Solution {

public:
    int singleNumber(vector<int>& nums) {
        int ans = 0;	//ans记录最终答案，初始化为0
        // 考虑每个数二进制某一位上出现 1 的次数，如果出现 1 的次数为 3k + 1，则证明只出现一次的数这一位是 1
        for (int bit = 0; bit < 32; bit++) {	//int类型数据是4B,即32位，所以这里我们需要遍历32位
            int count = 0;	//count记录每一位上1的个数
            for (int i = 0; i < nums.size(); i++)	//遍历整个数组，累积计算这一位上1的个数
                count += (nums[i] >> bit) & 1;	//累积计算这一位上1的个数，注意是右移
            ans += (count % 3) << bit;	//累积答案，注意右移bit位
        }

        return ans;	//最后返回答案
    }
};

算法三：暴力解：

class Solution {
    public int singleNumber(int[] nums) {
        if(nums.length==1){
            return nums[0];
        }
        Arrays.sort(nums);
        for(int i = 0; i< nums.length-1;i+=3){
            if(nums[i]!=nums[i+2]){
                return nums[i];
            }
        }
        return nums[nums.length-1];
    }
}

2021年8月28日13:11:06：

190. 颠倒二进制位

颠倒给定的 32 位无符号整数的二进制位。

示例 1：

输入: 00000010100101000001111010011100
输出: 00111001011110000010100101000000
解释: 输入的二进制串 00000010100101000001111010011100 表示无符号整数 43261596，
     因此返回 964176192，其二进制表示形式为 00111001011110000010100101000000。

示例 2：

输入：11111111111111111111111111111101
输出：10111111111111111111111111111111
解释：输入的二进制串 11111111111111111111111111111101 表示无符号整数 4294967293，
     因此返回 3221225471 其二进制表示形式为 10111111111111111111111111111111 。

算法分析

1、n >> i & 1表示的是取二进制位的第i位的值。
2、从低位到高位依次取每一位，接在res二进制的后面， 每次拼接时res需要进行res << 1操作

代码：

class Solution {
public:
    uint32_t reverseBits(uint32_t n) {
        uint32_t res=0;    //定义答案，也是无符号整数。
        for(int i=0;i<32;i++){  //从最低位到最高位依次取出每一位。
            res=((res<<1)+(n>>i&1));  //res更新为res先左移一位再加上当前为上的数（要么0，要么1） ，
            //加上0即意味着只是将res左移一位，加上1意味着不仅是将res左移一位同时加上了一个数。        
        }
        return res;    //将答案记得返回。
    }
};

2021年8月28日16:55:25：

//我们可以将int转为字符串，再翻转字符串，最后再将字符串转为int即可，我们在做的时候可以直接使用位运算的操作(这个题目用到了左移右移<<,>>,&)，省去中间两个步骤，即直接将int翻转得到int
//我们在做的时候，取n的第k位上的数(即(n>>k)&1,即是n右移k位和1相与&,就可以得到n的第k位上的数字)，然后我们定义答案res,
//我们在做的时候相当于将原数的最低位取出来放到新数的最高位，然后再取次低位放到最高位的后面一位，然后再取次次低位放到最高位后面一位的后面一位，......
//每一次就相当于在答案新数res的后面加一位，即是说：我们先把后一位空出来即res<<1，将res左移一位，再加上(n>>k&1),
//做的时候就是将原数从低位到高位遍历，使用(n>>k&1)取出n的每一位，取出n的每一位之后我们依次加到res的后面，即res<<1+(n>>k&1),
public class Solution {
    // you need treat n as an unsigned value
    public int reverseBits(int n) {
        int res=0;  //定义答案
        for(int k=0;k<32;k++){  //原数一共32位，我们需要移动32次
            res=(res<<1)+((n>>k)&1);  //先将res左移一位之后再将n右移k位之后的结果与上1再加到res后面,注意<<,>>的优先级很低，所以我们要加上（）
        }  
        return res; //最后将res返回
    }
}

191. 位1的个数

编写一个函数，输入是一个无符号整数（以二进制串的形式），返回其二进制表达式中数字位数为 ‘1’ 的个数（也被称为汉明重量）。

示例 1：

输入：00000000000000000000000000001011
输出：3
解释：输入的二进制串 00000000000000000000000000001011 中，共有三位为 '1'。

示例 2：

输入：00000000000000000000000010000000
输出：1
解释：输入的二进制串 00000000000000000000000010000000 中，共有一位为 '1'。

示例 3：

输入：11111111111111111111111111111101
输出：31
解释：输入的二进制串 11111111111111111111111111111101 中，共有 31 位为 '1'。

提示：

输入必须是长度为 32 的 二进制串 。

算法一：我们使用n>>k&1取出n的每一位如果为q，则答案加一

class Solution {
public:
    int hammingWeight(uint32_t n) {
        uint32_t res=0;  //定义答案即1的个数，初始化为0个。
        for(int i=0;i<32;i++){
            int a=n>>i&1;   //依次取出n的32位二进制数
            if(a==1) res++;    //如果a是1，答案加一。
        }
        return res;
    }
};

算法二：lowbit(x)操作：返回x&(-x)
每次我们减去一次(x&-x），直到x为零为止。
代码：

class Solution {
public:
    int hammingWeight(uint32_t n) {
        uint32_t res=0;    //记录答案，即1的个数。注意输入的是二进制数。
        while(n) {
            n-=(n&-n);    //注意输入的是二进制数，(n&-n)得到是最后一位1及其之后的0，不断减去lowbit(),每减一次，1的个数就多一个，我们每次减去100...00，直到n为0。
            //不理解的话自己举个例子即可（如10100）。
            res++;  
        }
        return res;
    }
};

2021年8月28日17:34:58：

//我们可以依次枚举n的每一位(一共32位)，如果是1就让res加一，或者使用lowbit操作即可实现
//解法一：
/**
public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        int res=0;
        for(int i=0;i<32;i++){
            if(((n>>i)&1)==1) res++;
        }
        return res;
    }
}
 */

 //解法二：使用lowbit操作，lowbit操作可以返回数字n的最后一位1及其后面的0，即是二进制表示中最右边的1，如：1101000，lowbit操作之后返回1000，
 //这样我们每次让n-lowbit(n)即可，直到n被减到0，n被减了多少次，n就有多少个1。对x进行lowbit操作即是x&(-x+1),即x和-x+1进行相与&操作，这样就可以得到上面例子中的1000
 //比如说：x=......100000,则-x=``````011111(``````就是......的取反的意思hhh),则-x+1就是``````100000,则将x和-x+1进行相与&结果就是：
 //x&(-x+1):000000100000(&与操作必须两者都是1结果才是1，只要有一个为0结果就是0),我们发现结果就是返回了x的最后一位1和这个1之后的0
 //注意哈：在计算机里面：取反x加一就相当于是负x,因为在计算机中负x的补码就是取反x加一，所以我们这里的运算就是x&(-x),就可以得到x的最后一位1
 //这样写的计算次数就比上面的写法的32次算一下，其计算次数等于n中的1的个数
 public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        int res=0;
        while(n!=0) {  //直到n被减到0为止
            n-=(n&(-n));  //每次n减去lowbit(n)
            res++;  //每运算一次res就加一
        }
        return res;
    }   
}

201. 数字范围按位与（*）

给定范围 [m, n]，其中 0 <= m <= n <= 2147483647（2^31-1），返回此范围内所有数字的按位与（包含 m, n 两端点）。

示例 1: 

输入: [5,7]
输出: 4

示例 2:

输入: [0,1]
输出: 0

&运算具有交换性。

算法分析

• 1、求[m, n]之间所有数的按位与，首先对于n和m这两个数在第i位前面都相同，由于n > m，因此n的第i位是1，m的第i位是0,即m = xxx0...，n = xxx1...(...表示后面是什么未知)，因此一定会存在一个数是t = xxx1000的形式，即这个数的第i位是1，且后面的都是0的形式，并且这个数t一定在[m,n]内
• 2、这样的话[m,n]中的所有数与t按位与后再第i位以至后面全是0，因此只需求两个数的公共前缀即可。

代码：

class Solution {
public:
    int rangeBitwiseAnd(int m, int n) {
        int res=0;  //定义答案；
        for(int i=30;i>=0;i--){  //数最大为2^31-1,所以我们从最高位开始找第一个m,n数位上的数不相同的数，
            if((m>>i&1)!=(n>>i&1)) break; //如果m的第i位和n的第i位不同，即找到了m,n不同的最高位，终止;
            if(((m>>i)&1)!=0) res+=(1<<i);   //如果当前位上的数是1的话，我们就将当前位上的数加到答案上。注意这里是将1左移i位。并且注意这里判断的是m,不是n，因为m更小。
            //如果是0的话就不用管了。
        }
        return res;    //记得将答案返回。
    }
};

2021年8月28日17:45:37：

至于为什么m,n不相同的那一位结果也是0， 因为与运算有交换律，所以我们让m,n的那一位相与结果就是0，再来其他数也不行，结果就是0了

//比如说是[3,7],我们就需要返回3^4^5^6^7,我们我们直接循环取相与的话，由于数据量最大大于一亿，所以会超时，我们要优化，
class Solution {
    public int rangeBitwiseAnd(int m, int n) {
        int res=0;  //定义答案res
        for(int i=30;i>=0;i--){ //从最高位即第30位开始从高位往低位遍历
            if(((m>>i)&1)!=((n>>i)&1)) break;  //我们先判断不相等，如果m的第i位和n的第i位上的数不一样了，我们就直接结束，因为从这一位开始后面都是0
            //否则m的第i位就和n的第i位相同，我们就再判断一下这一位上是否为1，如果是1的话，我们就累加到res上,如果是0我们就不用管
            if(((m>>i)&1)==1) res+=(1<<i);  //注意注意注意必须这一位上是1才累加到res上，如果这一位上是0的话，我们就不能累加1<<i位到res上，否则答案就是错的
        }
        return res; //最后将答案返回即可
    }
}

2021年11月9日20:57:26：

class Solution {

//我们先看m,n这两个数,首先m,n至少有一位是不同的,比如说m=xxxxx0...... , n=xxxxx1.....,xxxxx表示m,n的前k位是相同的,第k+1位不同,首先第k位由于m,n不同,所以最终结果中的第k位一定是0
//我们再考虑这样两个数,首先是xxxxx01111..111这个数,这个数必然是>=m的且是小于n的,因为这个数是m=xxxxx0......这个形式的最大的数,
//同理xxxxx10000...000这个数肯定是<=n的,且大于m,因为这个数是n=xxxxx1......这个形式的最小数,所以这两个数一定是在m,n之间的,
//我们考虑将这两个数进行异或则结果就是xxxxx0 0000...000,第一个零是m,n第k位异或的结果，后面的0是那两个特殊的数异或的结果
//而下面的xxxxx最后的结果还是xxxxx,所以这个题目的答案就是我们从高位到低位找到m,n第一位不一样的位，从这一位之后都是0，前面的相同的数就是答案

    public int rangeBitwiseAnd(int m, int n) {
        int res=0;
        for(int i=30;i>=0;i--){ //最大是2^31-1,所以最高位是30(下标从0开始)
            if(((m>>i)&1)!=((n>>i)&1)) break;  //第i位m,n上的数不同，则从这一位开始最后的结果后面都将是0
            else {  //否则m,n的第i位是相同的，我们再判断一下如果这一位上是1的话，我们就在最后结果中加上1<<i，注意是1左移位
                if(((m>>i)&1)!=0) res+=(1<<i);
            }
        }
        return res; //最后的结果就是res
    }
}

231. 2的幂

给定一个整数，编写一个函数来判断它是否是 2 的幂次方。

示例 1:
输入: 1
输出: true
解释: 2^0 = 1

示例 2:
输入: 16
输出: true
解释: 2^4 = 16

示例 3:
输入: 218
输出: false

首先n一定是正数，如果是负数，直接返回false即可。

代码：

class Solution {
public:
    int lowbit(int x){
        return x&-x;    //编写lowbit操作。
    }
    bool isPowerOfTwo(int n) {
        if(n<=0) return false;  //如果n<=0，则一定不是2的幂次方。
        if(lowbit(n)==n) return true;   //如果lowbit(n)==n,则n是2的整数次幂，返回true。
        else return false;  //不等于就不是2的整数次幂。返回false；
    }
};

时间复杂度：O(1);

2021年8月28日20:29:13：

/**
方法一：
class Solution {
    public boolean isPowerOfTwo(int n) {
        if(n<=0) return false;
        while(n%2==0) n/=2;
        return n==1;
    }
}
 */

//方法二：使用lowbit操作：首先如果是2的整次幂，一定>0, 如果是0或者负数则一定不是2的整次幂，注意0~1之间的数有可能是2的整次幂，比如2^-1=1/2,
//如果一个数是2的整次幂，则其二进制表示一定是100...00的结构，lowbit(x)=x&(-x)，其会返回这个数的最后一个1，所以如果一个数是2的整次幂，则我们调用lowbit(x)，
//其应该就是返回100...00,即x本身，所以我们只需要判断一下lowbit(x)和x是否相同即可，如果相同，就是2的整次幂，
class Solution {
    public boolean isPowerOfTwo(int n) {
        if(n<=0) return false;  //如果n<=0则一定不是2的整次幂，我们返回false
        return n==(n&(-n)); //否则只需要看一下n是否和lowbit(n)是否相同，相同返回true,否则返回false
    }
}

递归解决：

bool isPowerOfTwo(int n){
    if(n==1) return true;
    if(n==0) return false;
	if(n%2!=0) return false;
	return isPowerOfTwo(n/2);
}

260. 只出现一次的数字 III

给定一个整数数组 nums，其中恰好有两个元素只出现一次，其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序
返回答案。

进阶：你的算法应该具有线性时间复杂度。你能否仅使用常数空间复杂度来实现？

 示例 1：

输入：nums = [1,2,1,3,2,5]
输出：[3,5]
解释：[5, 3] 也是有效的答案。

示例 2：

输入：nums = [-1,0]
输出：[-1,0]

示例 3：

输入：nums = [0,1]
输出：[1,0]

提示：

2 <= nums.length <= 3 * 104
-231 <= nums[i] <= 231 - 1
除两个只出现一次的整数外，nums 中的其他数字都出现两次

1、对所有数字进行异或处理，最后得到的一定是a ^ b，且a ^ b != 0
2、在a ^ b结果中，任意找到某位不相同的位置t，可以通过该位区分出这两个数
3、再次通过枚举所有数，把第t位是0的所有数（一定不包括b）异或起来就会得到a，把第t位是1的所有数（一定不包括a）异或起来就会得到b
时间复杂度 O(n)
空间复杂度 O(1)

代码：

class Solution {
public:
    int get(vector<int>& nums,int k,int t){
        int result=0;  //定义每次调用的结果。
        for(auto x:nums){   //遍历整个数组。
            if((x>>k&1)==t){    //每次把第k位等于t的数进行异或。
                result^=x; 
            }
        }
        return result;
    }
    vector<int> singleNumber(vector<int>& nums) {
        int res=0;  //定义
        for(auto x:nums){
            res^=x;     //对所有数进行异或操作，最终结果是a^b的异或（同0异1）结果。
        }
        int k=0;    //我们从最低位开始查找a,b的二进制不同的最低的那一位，
        while((res>>k&1)==0) k++;    //如果a,b的异或结果为0,说明a，b在这一位上的数相同，不是我们所需要的，我们让k++，继续往后判断。==运算符优先级高于&,所以我们要加括号。
        //while循环结束，得到的k就是a,b数位不同的最低位位数。
        return {get(nums,k,0),get(nums,k,1)};   //编写get函数，对第k位上等于0的数进行异或得到a,对第k位上等于1的数进行异或得到b;
        //调用两次get函数，每次分别得到a,b;
    }
};

2021年8月28日13:14:55：

//这个题目是：有两个元素只出现一次,其余所有元素均出现两次,找出只出现一次的那两个元素,这个题目我们将所有数异或的结果就是a^b(a,b是那两个元素),由于a!=b,所以a^b!=0
//a,b不同，这就意味着a和b的二进制表示中至少有一位是不一样的，
class Solution {
    public int[] singleNumber(int[] nums) {
        int res=0;  //res记录数组中所有数异或的结果，即最后就是a,b异或的结果
        for(int x:nums) res^=x; //将数组中的所有数进行异或
        int k=0; //从低位(第0位)开始寻找a,b哪一位数不同,即res的哪一位为1(同零异一)
        while(((res>>k)&1)==0) k++; //只要res的这一位为0，我们就往高位移动(注意是k++,不是k--),直到res的这一位为1，当k停下来的时候，第k位就是res为1的位数，即是a,b位不同的位数
        //注意while循环是一定会停下来的，因为a,b是不同的，所以a,b异或之后至少有一位不同，当找到这一位之后，k就一定会停下来，最多32次
        int a=get(nums,k,0);  //自己编写get函数，因为求a,b都需要使用到这个函数，所以我们直接自己定义出来，参数k即第k位不同，参数0即是第k位为0，得到的数即是a
        int b=get(nums,k,1);  //参数1即是第k位为1，得到的数即是b 
        return new int[]{a,b};  //最后将a,b构造成数组进行返回
    }
    public int get(int[] nums,int k,int u){ //u根据传入的参数不同，可能取0或者1
        int ans=0;  //记录本次答案，即u=0,res得到a,u=1,res得到b,
        for(int x:nums){  //遍历数组中每一个数，
            if(((x>>k)&1)==u){  //如果x的第k位=0，注意这里是根据u的取值不同，取的值是不同的
                ans^=x; //将满足条件的数x进行异或
            }
        }
        return ans; //异或之后得到的数就是a或者b将其进行返回
    }
}

解法二：也可以使用lowbi操作得到res的最右边的一位1：

class Solution {
    public int[] singleNumber(int[] nums) {
        int s = 0;
        for (int num : nums) {
            s ^= num;
        }

        int lowbit = s & (-s);	//lowbit即是a,b不为0的位数,lowbit得到的就是000100000
        int res = 0;
        for (int num : nums) {
            if ((lowbit & num) == 0) res ^= num;  //这样得到的res即是b,最后b再和res相与得到的即是a
        }
        return new int[]{res, res ^ s};	
    }

268. 丢失的数字

给定一个包含 [0, n] 中 n 个数的数组 nums ，找出 [0, n] 这个范围内没有出现在数组中的那个数。

进阶：
你能否实现线性时间复杂度、仅使用额外常数空间的算法解决此问题?

示例 1：

输入：nums = [3,0,1]
输出：2
解释：n = 3，因为有 3 个数字，所以所有的数字都在范围 [0,3] 内。2 是丢失的数字，因为它没有出现在 nums 中。

示例 2：

输入：nums = [0,1]
输出：2
解释：n = 2，因为有 2 个数字，所以所有的数字都在范围 [0,2] 内。2 是丢失的数字，因为它没有出现在 nums 中。

示例 3：

输入：nums = [9,6,4,2,3,5,7,0,1]
输出：8
解释：n = 9，因为有 9 个数字，所以所有的数字都在范围 [0,9] 内。8 是丢失的数字，因为它没有出现在 nums 中。

示例 4：

输入：nums = [0]
输出：1
解释：n = 1，因为有 1 个数字，所以所有的数字都在范围 [0,1] 内。1 是丢失的数字，因为它没有出现在 nums 中。

提示：

n == nums.length
1 <= n <= 10^4
0 <= nums[i] <= n
nums 中的所有数字都 独一无二

这样时间复杂度为O(n),空间复杂度为O(1);
代码：

class Solution {
public:
    int missingNumber(vector<int>& nums) {
        int n=nums.size();  //注意n的值为数组长度，
        int sum=n*(n+1)/2;  //记录总和
        int s=0;    //s为实际这些数的总和
        for(auto x:nums){
            s+=x; 
        }
        return sum-s;   //得到缺少的数。
    }
};

2021年8月28日20:50:25：

//方法一：使用数学公式
//可以使用哈希表，时空间都是O(n), 这个题目和抽屉原理那个题目没有任何关系，这个题目要求O(n)时间，O(1)空间，我们可以累加0,1,2,...,n-1,n这n+1个数的总和即n*(n+1)/2
//假设数组中n个数的总和是S,则缺失的那个数就是n(n+1)/2-S;
/**
class Solution {
    public int missingNumber(int[] nums) {
        int n=nums.length;  //注意数组的长度n就是我们要计算的那个n(n+1)/2的那个n，不是n+1,就是n,因为这个数组中是包含0了，
        int res=n*(n+1)/2;  //res是0,1,2,.....,n这些数的总和
        int S=0;  //S累积数组中数的总和
        for(int x:nums) S+=x;
        return res-S;   //作差就是答案
    }
}
 */

 //上面的做法中当n很大时会溢出，可以转为long处理，我们还可以使用位运算求解,类似于只出现一次的数字那个题目
class Solution {
    public int missingNumber(int[] nums) {
        int res = nums.length;
        for (int i = 0; i < nums.length; ++i){
            res ^= nums[i];
            res ^= i;
        }
        //经过上面的操作，我们发现除了缺失的那个数字只被异或了一次，其他数(0~n，除了缺失值)都被异或了两次，所以得到的结果就是缺失值
        //这样写就不会溢出了
        return res;
    }
}

289. 生命游戏

2021年11月10日10:29:50：

class Solution {

//注意不能新开数组(题目要求),并且不能修改原数组(否则会影响下面细胞的状态),每一个b[i][j]都是int类型的,即都是32位的,而这个题目每一个格子只有0,1两种状态
//即只用了最后一位,所以我们可以继续使用原数组，我们使用其每一个数字的倒数第2位即可，比如之前是000...0001,并且之后其活，我们就用000...0011表示其之后的状态
//这样操作既不会影响其之后细胞的状态(看最后一位即可)，也可以知道这个细胞最后的状态(看倒数第二位即可,把倒数第二位移到个位就可以看了)
//

    public void gameOfLife(int[][] b) {
        int n=b.length,m=b[0].length;
        int[] dx={-1,-1,-1,0,0,1,1,1},dy={-1,0,1,-1,1,-1,0,1};  //方向数组，共8个方向
        for(int i=0;i<n;i++){  
            for(int j=0;j<m;j++){ //看一个细胞之后的存活状态
                int cnt=0; //cnt统计这个细胞周围8个格子的活细胞的数量
                for(int k=0;k<8;k++){
                    int p=i+dx[k],q=j+dy[k];
                    if(p>=0&&p<n&&q>=0&&q<m&&((b[p][q]&1)!=0)) cnt++; //注意要取个位，即b[p][q]要和q相与&,因为这个位置上可能已经被我们修改的倒数第二位
                }
                int cur=b[i][j]&1,next=0; //cur是当前细胞的状态，next是这个细胞之后的状态
                if(cur==1){ //分两种情况，即当前细胞是活着或者是死亡
                    if(cnt>3||cnt<2) next=0;
                    else next=1;
                }else{
                    if(cnt==3) next=1;
                    else next=0;
                }
                //求完next之后，我们要把next存到倒数第二位
                b[i][j] |=(next<<1); //把next左移一位再和b[i][j]进行或，就可以把其最后的状态存到其十位上了
            }
        }

        //最后再根据每一个细胞的倒数第二位的状态更新原数组
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                b[i][j]>>=1;
            }
        }
        //返回为空，不需要写返回值
    }
}

318. 最大单词长度乘积（二进制位存状态，类似于bitmap）

2021年11月10日10:03:59：

class Solution {

//由于每一个单词只包含小写字母,而小写字母只有26个,题目要求要找的两个单词中不能含有公共字母,
//这个题目的难点就变成了如何快速的判断两个字符串是否含有公共字母,我们可以使用二进制的思想,我们用一个长度为26的二进制数,即类似于bitmap的思想来表示26个字母出现的各种情况
//如果对应位置上的字母出现了就写1,没有出现就写0,这样每一个字符串都可以对应一个长度为26的二进制数,如101就表示有字母a和c
//这样当我们想判断两个字符串x,y是否有交集的时候.直接使用x&y就可以了,如果x&y不是0就有交集,没有交集的话就是0,如101和010相与就是0,这两个没有交集

    public int maxProduct(String[] words) {
        int n=words.length;
        List<Integer> st=new ArrayList<>(); //数组st存储单词列表中每一个字符串对应的26位二进制数
        for(String w:words){  //枚举单词列表中的每一个单词
            int s=0;  //s记录字符串w对应的26位的二进制数
            for(char c:w.toCharArray()){ //枚举单词w的每一个字母
                int t=c-'a';  //t是字母c的偏移位数
                s |=(1<<t); //在s上或(|)上这个100..00,
            }
            st.add(s); //最后别忘了将这个单词对应的26位的二进制数加到数组st中
        }

        int res=0;  //res记录最大长度
        //之后就要使用双重for循环枚举单词列表中的任意两个单词的相乘的长度了
        for(int i=0;i<n;i++){
            for(int j=i+1;j<n;j++){
                if((st.get(i)&st.get(j))==0) res=Math.max(res,words[i].length()*words[j].length()); //如果两个字符串相与的结果是0，就说明两个字符串没有交集，我们就用其长度之积更新res
            }
        }
        return res; //最后返回res
    }
}

338. 比特位计数

给定一个非负整数 num。对于 0 ≤ i ≤ num 范围中的每个数字 i ，计算其二进制数中的 1 的数目并将它们作为数组返回。

示例 1:

输入: 2
输出: [0,1,1]

示例 2:

输入: 5
输出: [0,1,1,2,1,2]

代码：

class Solution {
public:
    vector<int> countBits(int num) {
        vector<int> f(num+1,0); //申请一个大小为num+1(注意从0开始，所以大小加1), 且所有值均初始化为0；用于记录各个数字1的个数。
        for(int i=1;i<=num;i++){    //从1开始枚举，一直枚举到num。
            f[i]=f[i>>1]+(i&1);   //递推表达式。
        }
        return f;   //最后将答案数组返回。
    }
};

2021年8月28日21:01:25：

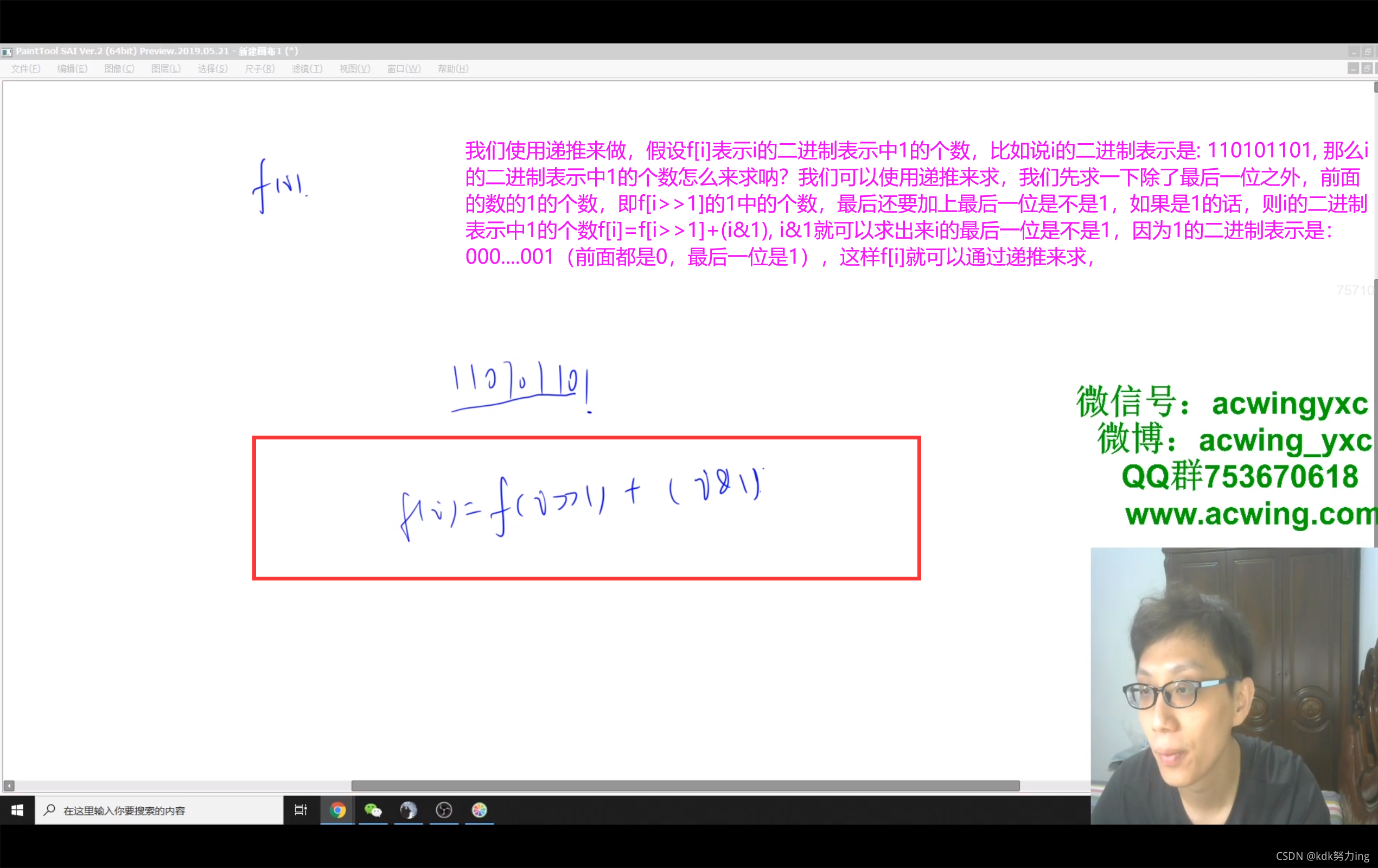
时空间复杂度都是O(n)

//使用递推来求：f[i]表示i的二进制表示中1的个数，从小到大依次递推出来f数组
class Solution {
    public int[] countBits(int n) {
        int[] f=new int[n+1]; //注意f数组的长度是n+1,因为题目求的是从0到n的二进制表示的数目,f数组初始化时都为0，并且f[0]=0,所以我们没有必要再显示初始化f[0]了
        for(int i=1;i<=n;i++){  //我们要递推出来整个从0到n的数组的值，即从0到n的二进制表示中1的个数，而f[0]我们已经知道了，所以我们这里要从1枚举到n
            f[i]=f[i>>1]+(i&1); //递推更新f数组，看图上的分析
        }
        return f; //最后将f数组返回

    }
}

算法二：
(位运算) O(n)
本题只需利用位运算的一个小技巧： a&(a−1)恰好消去了a最靠近右边的1，所以a的二进制表示中1的个数比 a&(a−1)多1个。
比如11&10=10，110&101=100。

class Solution {
public:
    vector<int> countBits(int num) {
        vector<int> res(num + 1, 0);
        for (int i = 1; i <= num; ++i) {
            res[i] = res[i & (i - 1)] + 1;	//新的方式更新f数组
        }
        return res;
    }
};

342. 4的幂

给定一个整数，写一个函数来判断它是否是 4 的幂次方。如果是，返回 true ；否则，返回 false 。

整数 n 是 4 的幂次方需满足：存在整数 x 使得 n == 4^x

示例 1：

输入：n = 16
输出：true

示例 2：

输入：n = 5
输出：false

示例 3：

输入：n = 1
输出：true

提示：

-2^31 <= n <= 2^31 - 1

代码：

class Solution {
public:
    bool isPowerOfFour(int n) {
        if(n<=0) return false;  //如果n<=0,则一定不是4的整次幂；
        if((n&(-n))!=n) return false;   //如果n不是2的整数次幂，则一定不是4的整次幂。
        int r=sqrt(n);  //这两句代码是判断其是否是平方数，即其开方之后还能否变回本身，如16开方之后为4,4*4为其本身，8开方之后是2点多，再平方之后不是其本身
        if(r*r!=n) return false;
        else return true;   //如果以上三个if条件全部满足，则一定是4的整数次幂。
    }
};

2021年8月28日21:33:49：

//题目要求我们不能使用循环或者递归，如果一个数可以表示成4的整次幂，即n=4^k=2^2k=(2^k)^2,即这个数一定可以表示成2的2k次幂，和2k的平方，
//所以一个数是4的整次幂的条件就是:1.>0， 2.只包含因子2， 3.是一个平方数，
class Solution {
    public boolean isPowerOfFour(int n) {
        if(n<=0) return false;
        //判断是否是平方数
        int r=(int)Math.sqrt(n); //求n的开方,注意java中Math.sqrt(x)返回是double型，我们要强制转换为int
        if(r*r!=n) return false;  //如果开完方回不去了，就不是平方数
        //判断是否是2的幂，可以使用lowbit或者2^30能否整除n
        if((1<<30)%n!=0) return false; //如果2的30次幂能够整除n,上面n是2的整次幂，否则不是
        //上面三个都满足了，才是4的整次幂，返回true
        return true;
    }
}

371. 两整数之和

不使用运算符 + 和 - ​​​​​​​，计算两整数 ​​​​​​​a 、b ​​​​​​​之和。

示例 1:

输入: a = 1, b = 2
输出: 3

示例 2:

输入: a = -2, b = 3
输出: 1

代码：

class Solution {
public:
    int getSum(int a, int b) {
        if(!a) return b;    //进位为0，则结束。
        int sum=(a^b),carry=(unsigned)(a&b)<<1; //sum记录总和，carry记录进位，且进位左移一位可能溢出，所以我们将其转化为无符号整型。
        return getSum(carry,sum);  //a是进位，b是总和。递归计算
    }
};

2021年8月29日09:54:32：

//不让使用+，-，我们可以使用位运算的方法，a^b，异或(同零异一)又叫不进位的加法，再加上进位即可，使用递归
class Solution {
    public int getSum(int a, int b) {
        if(b==0) return a;  //如果b等于0，我们直接返回a,这也是递归结束的条件，我们之后在递归传参的时候，将b视为进位(a&b<<1),当进位为0的时候，只返回异或结果即可
        int sum=a^b,carry=(a&b)<<1; //sum是a与b异或的结果，carry是进位值
        return getSum(sum,carry);  //将sum和carry再传到getSum参数中，递归计算下去，当递归结束的时候就得到的a+b的值
    }
}

int getSum(int a, int b) 
{
    int sum, carry; 
    sum = a ^ b;  //异或这里可看做是相加但是不显现进位，比如5 ^ 3
                 /*0 1 0 1
                   0 0 1 1
                 ------------
                   0 1 1 0      
              上面的如果看成传统的加法，不就是1+1=2，进1得0，但是这里没有显示进位出来，仅是相加，0+1或者是1+0都不用进位*/
    
    carry = (a & b) << 1;
    
                //相与为了让进位显现出来，比如5 & 3
                /* 0 1 0 1
                   0 0 1 1
                 ------------
                   0 0 0 1
              上面的最低位1和1相与得1，而在二进制加法中，这里1+1也应该是要进位的，所以刚好吻合，但是这个进位1应该要再往前一位，所以左移一位*/
    
    if(carry != 0)  //经过上面这两步，如果进位不等于0，那么就是说还要把进位给加上去，所以用了尾递归，一直递归到进位是0。
    {
        return getSum(sum, carry);
    }
    return sum;
}

389. 找不同

给定两个字符串 s 和 t，它们只包含小写字母。

字符串 t 由字符串 s 随机重排，然后在随机位置添加一个字母。

请找出在 t 中被添加的字母。

示例 1：

输入：s = "abcd", t = "abcde"
输出："e"
解释：'e' 是那个被添加的字母。

示例 2：

输入：s = "", t = "y"
输出："y"

示例 3：

输入：s = "a", t = "aa"
输出："a"

示例 4：

输入：s = "ae", t = "aea"
输出："a"
 

提示：

0 <= s.length <= 1000
t.length == s.length + 1
s 和 t 只包含小写字母

这个题目除了多余的元素，其他元素在两个字符串出现的次数这和均为2，所以我们可以借鉴前面题的思路，对两个字符串都进行异或操作，结果剩余的就是多余的那个元素。
https://blog.youkuaiyun.com/wjf7496/article/details/109211379

代码：

//字符型数据也可以进行位运算。https://blog.youkuaiyun.com/wjf7496/article/details/109211379
class Solution {
public:
    char findTheDifference(string s, string t) {
        int res=0;   //记录答案
        for(auto c:s) res^=c;   //对两个字符串中所有字符进行异或操作，最后结果就是多出的那个元素。
        for(auto c:t) res^=c;
        return res; //最后记得将答案返回。这里返回的类型是char,会进行自动类型转换。
    }
};

java：

class Solution {
    public char findTheDifference(String s, String t) {
        int res = 0;
        for(char c: s.toCharArray()) res ^= (c-'a');	//java中不能直接对字符进行位运算，且迭代运算记得将其转为字符数组。
        for(char c: t.toCharArray()) res ^= (c-'a');
        return (char)(res+'a');		//+'a'转为字符，且记得进行强制类型转换。
    }
}

2021年8月29日11:05:53：

//可以使用哈希表来解决，
/**
class Solution {
    public char findTheDifference(String s, String t) {
        Map<Character,Integer> map=new HashMap<>();
        for(char c:t.toCharArray()) map.put(c,map.getOrDefault(c,0)+1); //先遍历t字符串，再遍历s字符串从哈希表中将s中的字符的个数减一，
        for(char c:s.toCharArray()) map.put(c,map.getOrDefault(c,0)-1);
        for(char c:t.toCharArray()){  //最后再遍历哈希表，注意这里哈希表中t字符串中的每一个字符都有，只不过其个数是0个，但是字符还是都有的，而不是没有，
        //所以下面的判断条件绝对不能是map.containsKey(c)是否为true,这样写的话，则每一个字符都包含，这一点之前都错过一次了
            if(map.get(c)>0){
                return c;
            }
        }
        return 'a';
    }
}
 */
 //也可以使用位运算来解决，即和只存在一个数的那个题目相同，我们将两个字符串中的每一个字符进行异或操作，最后得到的结果就是那个被添加的字符，
 class Solution {
    public char findTheDifference(String s, String t) {
        int res=0;  //我们定义答案，注意int型的0对应的字符是null,33对应的是！
        for(char c:s.toCharArray()) res^=c; //将字符串s中的每一个字符和res进行异或操作，注意这里进行异或操作的时候，是将字符c转为int进行异或操作
        for(char c:t.toCharArray()) res^=c; //将字符串t中的每一个字符和res进行异或操作，
        return (char)res; //最后res是int型，而结果要求是char型，所以我们要强制转为char，如将33强制转为char，结果就是！
    }
}

401. 二进制手表

2022年1月2日11:58:13：

class Solution {

//其实就是问我们从0:00到11:59这么多时间内有多少个时间中有n个灯是亮着的,也就是说在一天所有的分钟表示里面,有多少个时间的二进制表示里面恰好有n个1
//在做的时候就是要枚举一下二进制的所有情况,判断一下如果当前的二进制表示里面恰好有n个1,并且这个二进制表示的时间是合法的(0:00到11:59),那么我们就把这个时间输出即可


    public List<String> readBinaryWatch(int n) {
        List<String> res=new ArrayList<>(); //答案数组
        int t=1<<10;  //一共用10个灯,所以一共是用1<<10种表示的情况,即1024种
        for(int i=0;i<t;i++){  //枚举二进制表示的所有情况
            int s=0;  //s统计当前这种情况中1的个数
            for(int j=0;j<10;j++){ //枚举i的每一位
                if(((i>>j)&1)!=0) s++;  //累加i中的1的个数
            }
            if(s==n){ //只有当s=n的时候，i才是一种有效的时间
                int a=i>>6,b=i&63; //i右移6位得到的就是i的小时数,i&63(2^6=64)就是得到的就是分钟数,妙啊！！！tql
                if(a<12&&b<60){
                    if(b<10) res.add(a+":0"+b); //如果分钟数不够10就要补上一个0
                    else res.add(a+":"+b);//否则不补0
                }
            }
        }
        return res;
    }
}

405. 数字转换为十六进制数

给定一个整数，编写一个算法将这个数转换为十六进制数。对于负整数，我们通常使用 补码运算 方法。

注意:

• 十六进制中所有字母(a-f)都必须是小写。
• 十六进制字符串中不能包含多余的前导零。如果要转化的数为0，那么以单个字符’0’来表示；对于其他情况，十六进制字符串中的第一个字符将不会是0字符。
• 给定的数确保在32位有符号整数范围内。 不能使用任何由库提供的将数字直接转换或格式化为十六进制的方法。

示例 1：

输入:
26

输出:
"1a"

示例 2：

输入:
-1

输出:
"ffffffff"

2021年8月29日11:19:52：

//题目中说：对于负整数，我们通常使用 补码运算 方法。但是对于负数我们无需特殊处理，因为在计算机中int型变量在表示负数的时候，本身就是用补码表示的,
//但是在java中右移负数的时候可能有问题，我们应该使用>>>即无符号右移进行右移操作
//比如-1，在计算机中就是111...111，即32个1，我们将数字转为16进制数，其实就是将这32位分成8组，每组4位，即每一组都是0000~1111,转为0~9,a~f, 
class Solution {
    public String toHex(int n) {
        if(n==0) return "0";  //特殊情况，如果n是0，返回字符串"0"
        String res="";  //否则的话我们定义一下答案
        String nums="0123456789abcdefg";  //定义16进制答案的字符串表示，即16进制的每一个数字，从小到大表示，每4位二进制数对应着字符串中的一个字符
        while(n!=0){  //只要n不是0，我们就要取低4位
            res+=nums.charAt(n&(0xf)); //0xf即1111，n&0xf即取n的二进制表示的低4位的值，比如26:11010,低4位是1010，即是10，对应着nums字符串中的a
            n>>>=4;  //取完n的低4位就将n的低4位删除，即将n右移4位，继续取n的低4位,注意这里使用>>>进行右移，是为了处理负数的情况，即是>>>是无符号右移
        }
        //最后得到的字符串是反过来的，因为其个位在最前面，十位在后面，比如26得到了"al",而其实应该是la,所以我们要翻转字符串
        char[] c=res.toCharArray();
        int m=res.length();
        int l=0,r=m-1;
        while(l<r){
            char t=c[l];
            c[l]=c[r];
            c[r]=t;
            l++;r--;
        }
        String ans="";
        for(char t:c) ans+=t;
        return ans;
        //我们可以发现对字符串进行翻转操作，不仅麻烦，而且时间很慢，所以我们应该是用StringBuilder
    }
}

//StringBuilder只需要写10行代码

class Solution {
    public String toHex(int n) {
    	//分成8组，每组4位（取低4位，删除4位，最后字符串翻转)
        if(n==0) return "0";  //下面的循环中处理不了0的情况，0需要我们特判
        StringBuilder res=new StringBuilder("");
        String nums="0123456789abcdef";
        while(n!=0){
            res.append(nums.charAt(n&(0xf)));
            n>>>=4;	//无符号右移
        }
        return res.reverse().toString();
    }
}

2021年11月10日09:29:45：

class Solution {

//注意负数在计算机中是用补码表示的,所以负数无需特殊处理,把10进制转化为16进制,一共32位,每4位一组,共8组,注意使用无符号左/右移符号
//即把每4个0000~1111转化为对应的16进制数,

    public String toHex(int n) {
        if(n==0) return "0";  //特判0
        StringBuffer s=new StringBuffer("");  //定义答案
        char[] num={'0','1','2','3','4','5','6','7','8','9','a','b','c','d','e','f'};  //定义16进制的每一个数字
        while(n!=0){
            s.append(num[n&0xf]); //n&0xf即是取数字n的低4位的值,0xf即是1111
            n>>>=4;   //每取4位，n就要去掉低4位，即右移4位
        }  
        //最后的s是反过来的，所以我们需要翻转一下
        return s.reverse().toString();
    }
}

461. 汉明距离

两个整数之间的汉明距离指的是这两个数字对应二进制位不同的位置的数目。

给出两个整数 x 和 y，计算它们之间的汉明距离。

注意：
0 ≤ x, y < 2^31.

示例:

输入: x = 1, y = 4

输出: 2

解释:
1   (0 0 0 1)
4   (0 1 0 0)
       ↑   ↑

上面的箭头指出了对应二进制位不同的位置。

算法分析：

这个题目就是让我们判断一下x,y的二进制有多少位不同，不用把它们转为二进制数字，直接运用二进制的位运算即可(&,^,|,) 我们每次取x的最低位和y的最低位进行异或操作，异或操作的结果是同零异一，所以如果x和y的这一位不同，结果将是1，我们就将这个1累加到res上，之后再右移一位x,y, 直到它们都变成了0。

代码：

class Solution {
public:
    int hammingDistance(int x, int y) {
        int res=0;  //res记录答案
        while(x||y){    //x或者y中有一个不为零就要进行运算
            res+=(x&1)^(y&1);   //x&1即求出x的个位，y&1同理，^操作同零异一，即两者不相同就是1，
            x>>=1,y>>=1;    //将个位删掉
        }
        return res; //最后返回答案
    }
};

2021年8月29日11:16:25：

//看一下这两个数字对应二进制中有多少位不一样，我们每次看一下x,y的个位上的数是否相同即看x&1和y&1是否相同，不同res++, 之后再将x，y各左移一位
class Solution {
    public int hammingDistance(int x, int y) {
        int res=0;  //定义答案
        while(x!=0||y!=0){  //x，y中有一个不是0的时候我们就要看一下x,y的各个位上是否相同，
            if((x&1)!=(y&1)) res++;  //x和y的个位上的数不同，res就加一
            x>>=1;y>>=1;  //将x,y都移除个位，即将x,y分别右移一位，x,y都右移才是去掉个位，而不是左移
        }
        return res; //最后将答案res返回
    }
}

477. 汉明距离总和

2021年11月9日21:36:58：

class Solution {

//数据量是1万,所以n^2的复杂度会超时,这个题目我们考虑的不是每两个数之间的汉明距离,而是考虑的是每一位(每一位和每一位之间是独立的),即从第0位到第30位
//比如先看个位上两两之间的汉明距离是多少,比如有五个数:101,100,111,011,010,我们可以把这些数字分成两组：一组是个位数字是1的,一组是个位数字是0的
//组内的汉明距离是0,而组之间的汉明距离都是1,而组与组之间的任意两个数字组合的汉明距离都是1,比如说这五个数中个位数字是1的有3个数,是0的有2个数,则在个位上的汉明距离是2*3=6
//即对于每一位其汉明距离就是x*y,x是这些数中第i位是0的数有x个，y是指这些数中第i位是1的数有y个,我们累积每一位上的汉明距离即可

    public int totalHammingDistance(int[] nums) {
        int res=0;  //res记录答案
        for(int i=0;i<=30;i++){ //枚举每一位
            int x=0,y=0;  //x,y分别累加这一位上0的个数和1的个数
            for(int n:nums){  //枚举数组中的每一个数n
                if(((n>>i)&1)==0) x++; //如果n的第i位是0，x就加一
                else y++; //否则y加一
            } 
            res+=(x*y);  //别忘了累加x*y  
        }
        return res;
    }
}

476. 数字的补数

2021年11月9日21:50:58：

class Solution {

//注意这个题目不是整个将数字的全部32位取反，而是只看那些从第i位是1的位数开始看起，比如5=101，我们只把数字5的最后3位取反即可
//所以这个题目我们先看这个数有多少位，只把最后几位取反即可，

    public int findComplement(int num) {
        if(num==0) return 1;  //特判0的补数是1
        int tmp=num;  //下面num会被改变，所以我们先用tmp存下来num
        int n=0;  //先求出数字num的位数
        while(num!=0){
            num>>=1;
            n++;
        }
        return tmp^((1<<n)-1);
        //或者写：return (~tmp)&((1<<n)-1) //只对最后n位取反。1<<n-1是为了得到1000-1=111，最后我们和~tmp相与就是答案
    }
}

504. 七进制数

2022年1月2日14:12:33：

class Solution {
    public String convertToBase7(int n) {
        if(n==0) return "0";
        StringBuffer res=new StringBuffer("");
        int t=1;
        if(n<0){
            t=-1;
            n=-n;
        }
        while(n!=0){
            res.append(n%7+"");
            n/=7;
        }
        if(t<0) return "-"+res.reverse().toString();
        return res.reverse().toString();
    }
}

709. 转换成小写字母

2021年12月19日11:50:40：

class Solution {

//我们当然可以直接使用toLowerCase函数，但是肯定不是面试官想要的结果，一种更好的方法是观察小写字母和大写字母的 ASCII 码表示：

// 大写字母 A - Z 的 ASCII 码范围为 [65, 90]
// 小写字母 a - z 的 ASCII 码范围为 [97, 122]。

// 因此，如果我们发现 ch 的 ASCII 码在 [65, 96] 的范围内，那么我们将它的 ASCII 码增加 32，即可得到对应的小写字母。

// 近而我们可以发现，由于 [65, 96]对应的二进制表示为 [(01000001)_2, (01011010)_2]，32 对应的二进制表示为 (00100000)_2，而对于 [(01000001)_2, (01011010)_2内的所有数，表示 32 的那个二进制位都是 0，因此可以对 ch 的 ASCII 码与 32 做按位或运算，替代与 32 的加法运算，即可得到小写字母对应的的大写字母了。

    public String toLowerCase(String s) {
        int n=s.length();
        char[] c=s.toCharArray();
        String res="";
        for(int i=0;i<n;i++){
            int t=c[i]; //注意这里因为我们要用ASCII码(数字)做判断，所以这里是要用int型变量来接收c[i]
            if(t>=65&&t<=90){ //注意大写字母的范围是65~97,而小写祖母的范围是97~122
                t |=32; //大写字母就让其与32相与
            }
            res+=(char)t; //res要拼接上字符型的变量t
        }
        return res; //最后要返回res字符串
    }
}

腾讯： IP地址与int整数的转换

题目描述
ip地址与整数的转换。

例如，ip地址为10.0.3.193，把每段拆分成一个二进制形式组合起来为00001010 00000000 00000011 11000001，然后把这个二进制数转变成十进制整数就是167773121。

2021年12月19日22:07:03：
题目分析
借助位运算实现。如IP10.0.3.193，将10左移24位，0左移16位，3左移8位，193左移0位。4个seg或运算，即为结果。

public static void main(String[] args) {
        String ip=in.next();
        String[] s=ip.split("\\.");
        int a=Integer.valueOf(s[0])<<24;  //最高位左移24位
        int b=Integer.valueOf(s[1])<<16;  //次高位左移16位
        int c=Integer.valueOf(s[2])<<8; //第三高位左移8位
        int d=Integer.valueOf(s[3]);  //最低位不用左移
        int res=a|b|c|d;
        System.out.println(res);
    }

反过来，如何将整数转成IP

将整数和255做与运算，结果为IP的第4段（即最后/最低那一段）。整数右移8位，和255做与运算的结果就是IP的第3段…最后再将每轮与运算的结果拼接起来便是最终的IP地址。

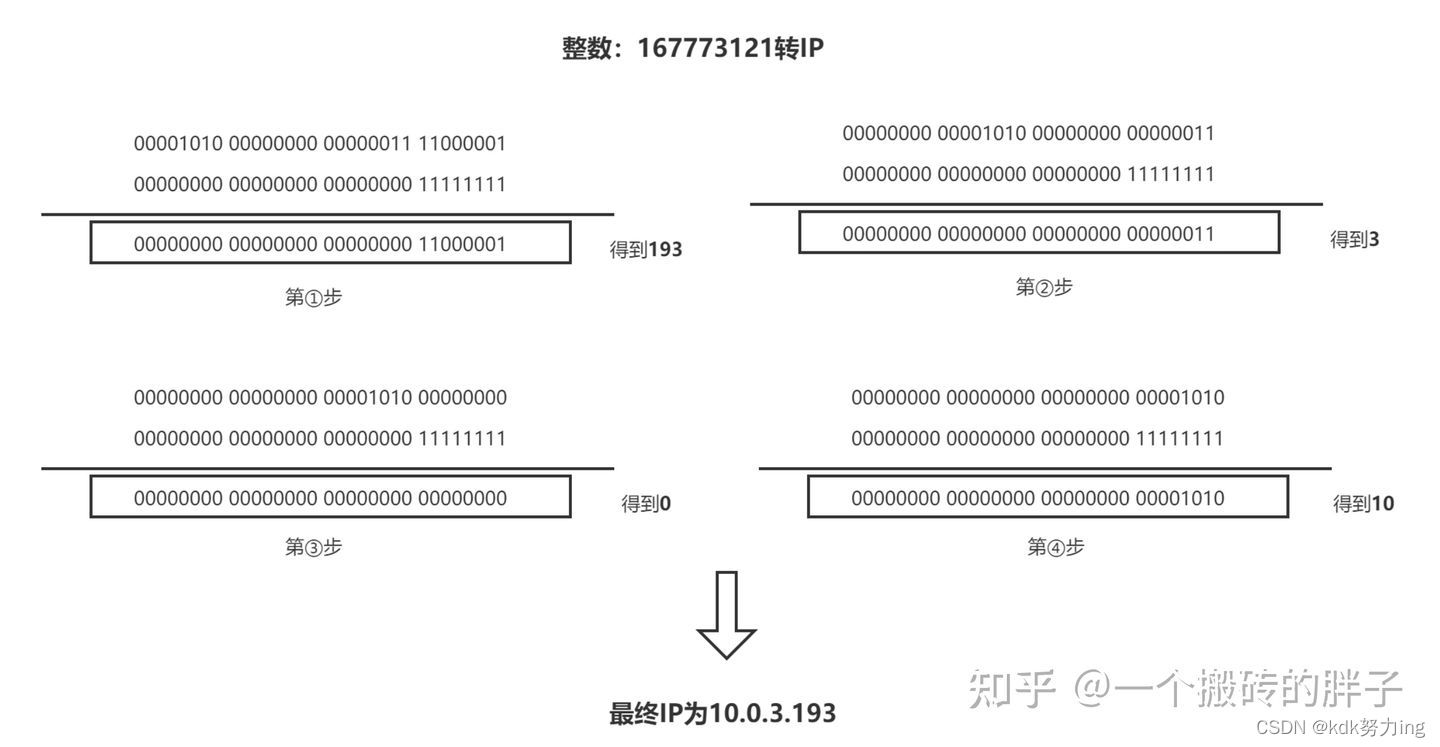
2021年12月19日22:23:57：

public static void main(String[] args) {
        int n=in.nextInt();
        StringBuffer res=new StringBuffer("");
        res.append(((n>>24)&255)+"."); //这是最高位
        res.append(((n>>16)&255)+"."); //这是第二段
        res.append(((n>>8)&255)+"."); //这是第三段
        res.append((n&255));  //这是最低位
        System.out.println(res);
    }