2024亚太地区数学建模竞赛（亚太杯）选题建议+初步分析-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_43345535/article/details/143930470

提示：C君认为的难度和开放度评级如下：

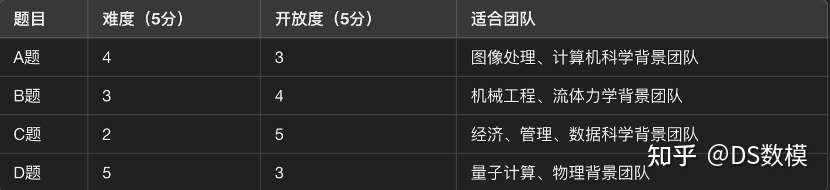
以下为ABCD题选题建议及初步分析：

A题：复杂场景下的水下图像增强研究

A题聚焦水下图像在复杂环境中的质量提升，属于图像处理与物理建模结合的经典问题。题目要求通过统计分析对图像降解问题进行分类（如色偏、低光和模糊），并基于物理模型构建降解模型，然后提出针对性的图像增强方法，最后验证效果。题目还需综合多种图像质量评价指标（如PSNR、UCIQE、UIQM）进行对比。核心难点在于处理复杂的水下环境对光学特性的影响，以及结合传统方法和深度学习进行增强算法设计。

建议有如下的建模过程：

l 数据分析与分类：对提供的图像进行多角度分析（直方图、边缘检测等），并依据降解特性分类。

l 降解建模：基于Jaffe-McGlamery物理模型，构建水下图像降解方程，分析光吸收和散射效应。

l 提出增强算法：根据不同场景问题（如色偏、模糊）设计增强方法，可选用传统图像处理或深度学习模型。

l 评价与优化：计算图像增强效果的PSNR、UCIQE、UIQM值，调整模型参数优化效果。

推荐的算法有：传统方法：直方图均衡化、拉普拉斯滤波、CLAHE（自适应直方图均衡化）、深度学习：基于GAN的对抗生成网络（如CycleGAN）、卷积神经网络（CNN）、优化算法：遗传算法用于调优模型参数。

这里尤其推荐利用深度学习中的GAN进行图像增强，该类方法效果较好。这道题目属于CV领域的题目，适合有基础的同学进行选择。

B题：三合一空调外形优化设计

B题是物理类+建模类题目。B题结合空气动力学与设备优化设计，探讨空调、加湿器和空气净化器三合一设备的外形优化。需考虑进出口位置、方向、风速、风量等参数对设备性能的影响，并基于仿真和数学建模优化设计外形，兼顾能效、舒适性及安全性。核心难点在于空气流体建模和多目标优化算法的结合。

建议有如下的建模过程：

l 物理建模：根据设备气流特性，构建基于Navier-Stokes方程的流体力学模型，描述空气流动及换热过程。

l 参数优化：对不同的外形设计进行仿真，优化气流分布与设备性能。

l 多目标优化：平衡设备能效（耗能最小）、舒适性（空气分布均匀）和安全性。

l 最优设计输出：提供设计方案的具体尺寸及外形参数，并进行仿真验证。

推荐的算法有：

流体仿真：CFD工具（如ANSYS Fluent）用于模拟气流、优化算法：遗传算法、粒子群优化（PSO）用于多目标参数优化、数据处理：Matlab或Python处理仿真数据。这里建模考虑的因素尽量越多越好，有物理实验背景，且具备良好数据分析与优化建模能力的团队可以优先选择。

C题：宠物产业及相关产业的发展分析与策略

这道题就是很多同学在训练的时候经常做的题目类型了，属于大数据、数据分析类题目，同时也是团队擅长的题目。需要一定的建模能力，和其他赛事赛题类型类似，建议数学、自动化、数据科学、计算机科学相关专业的同学。C题聚焦于宠物产业的发展与市场需求分析，要求基于历史数据分析产业趋势，构建预测模型并提供策略建议。题目需从多个维度（如宠物类型、市场需求）分析行业数据，同时需结合全球产业特点与中国市场现状，制定符合实际的商业发展策略。

推荐的建模过程：

l 数据分析：清理并处理提供的附件数据，分析宠物数量和市场变化趋势。

l 时间序列建模：构建ARIMA模型预测未来三年的宠物产业发展。

l 全球对比分析：结合欧美市场的宠物产业数据，建立回归模型预测全球宠物食品需求。

l 策略建议：分析出口数据与政策影响，提出产业发展建议。

这里推荐利用EDA进行分析，以及利用回归方法和时间序列模型，比如ARIMA模型或Prophet模型进行预测。

在开始大家需要对数据进行分析和数值化处理，也就是EDA（探索性数据分析）。并且可以使用一些可视化方法，可以使用常见的EDA可视化方法：

l 直方图和密度图：展示数值变量的分布情况。

l 散点图：展示两个连续变量之间的关系。

l 箱线图：展示数值变量的分布情况和异常值。

l 条形图和饼图：展示分类变量的分布情况。

l 折线图：展示随时间或顺序变化的趋势。