C - Train Problem II HDU - 1023 （有趣的卡特兰数）

最新推荐文章于 2020-03-30 22:49:35 发布

原创最新推荐文章于 2020-03-30 22:49:35 发布 · 166 阅读

0 ·

CC 4.0 BY-SA版权

数论专栏收录该内容

22 篇文章

订阅专栏

卡特兰数第一道题科普一下卡特兰数先；
卡特兰数的维基百科：https://zh.wikipedia.org/wiki/卡塔兰数
1-100的卡特兰数：http://blog.youkuaiyun.com/lttree/article/details/29392541
简单来讲卡特兰数就是
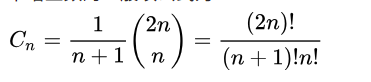
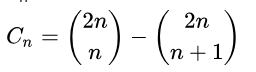
在这里插入图片描述

递推式cn=cn-1*(4*n-2)/(n+1);
常见应用：具体看维基百科，我的理解就是由两个相同数量的东西匹配而其中一个从前遍历一定比后面得多
1.栈的出入有多少的出去顺序。
2.dyck word数
3.合法运算式数
4.n个节点组成不同构二叉树的方案数
5.在n × n格点中不越过对角线的单调路径的个数
6.连结顶点而将n + 2边的凸多边形分成三角形的方法个数
7.Cn表示表为2×n的矩阵的标准杨氏矩阵的数量。也就是说，它是数字 1, 2, …, 2n 被放置在一个2×n的矩形中并保证每行每列的数字升序排列的方案数。
给个例题：C - Train Problem II HDU - 1023
链接：https://vjudge.net/contest/295931#problem/C
java实现
javatqlhttps://blog.youkuaiyun.com/qq_27599517/article/details/51027296
c++实现
将数字i的各个位数放在数组里然后乘除即可

#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
const int MAXN = 105;
int a[MAXN][MAXN];
///可以作为模板
void Catalan()
{
    int len=1,yushu=0;
    a[1][0]=1;
    a[1][1]=1;
    for(int i=2/*1*/;i<MAXN;i++){
        yushu=0;/**/
        for(int j=1;j<=len;j++)
        {
            int k=a[i-1][j]*(4*i-2)+yushu;
            a[i][j]=k%10;yushu=k/10;
        }
        while(yushu)
        {a[i][++len]=yushu%10;
        yushu/=10;}
        for(int j=len;j>=1;j--)
        {
            int k=a[i][j]+yushu*10;
            a[i][j]=k/(i+1)/*10*/;
            yushu=k%(i+1);
        }
        while(!a[i][len])
            len--;
        a[i][0]=len;
    }
}
int main()
{
    Catalan();
    int n;
    while(cin>>n)
    {
        for(int i=a[n][0]; i>0; i--)
            cout<<a[n][i];
        cout<<endl;
    }
    return 0;
}

优秀的题解https://blog.youkuaiyun.com/qingshui23/article/details/51001054