9 TensorFlow重要算法基础

实现最小二乘法

程序9-1：

import numpy as np
from matplotlib import pyplot as plt

A = np.array([[5],[4]])
C = np.array([[4],[6]])
B = A.T.dot(C)
AA = np.linalg.inv(A.T.dot(A))
l=AA.dot(B)
P=A.dot(l)
x=np.linspace(-2,2,10)
x.shape=(1,10)
xx=A.dot(x)
fig = plt.figure()
ax= fig.add_subplot(111)
ax.plot(xx[0,:],xx[1,:])
ax.plot(A[0],A[1],'ko')

ax.plot([C[0],P[0]],[C[1],P[1]],'r-o')
ax.plot([0,C[0]],[0,C[1]],'m-o')

ax.axvline(x=0,color='black')
ax.axhline(y=0,color='black')

margin=0.1
ax.text(A[0]+margin, A[1]+margin, r"A",fontsize=20)
ax.text(C[0]+margin, C[1]+margin, r"C",fontsize=20)
ax.text(P[0]+margin, P[1]+margin, r"P",fontsize=20)
ax.text(0+margin,0+margin,r"O",fontsize=20)
ax.text(0+margin,4+margin, r"y",fontsize=20)
ax.text(4+margin,0+margin, r"x",fontsize=20)
plt.xticks(np.arange(-2,3))
plt.yticks(np.arange(-2,3))

ax.axis('equal')
plt.show()

结果：

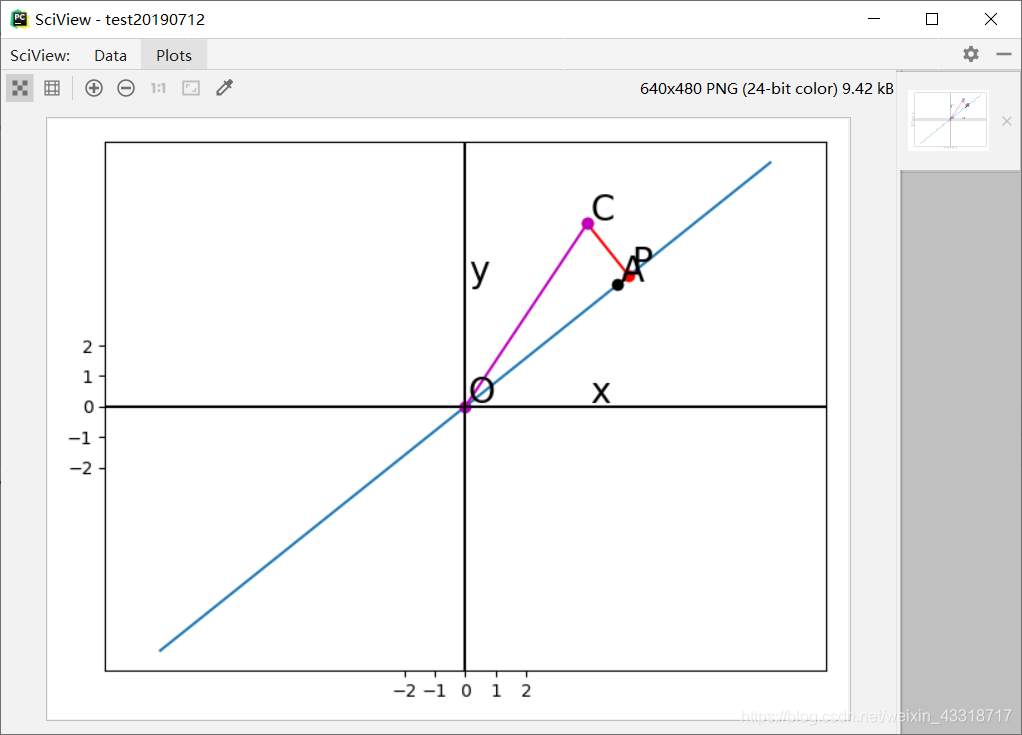
随机梯度下降算法实现
程序9-2：

x = [(2, 0, 3), (1, 0, 3), (1, 1, 3), (1,4, 2), (1, 2, 4)]
y = [5, 6, 8, 10, 11]

epsilon = 0.002

alpha = 0.02
diff = [0, 0]
max_itor = 1000
error0 = 0
error1 = 0
cnt = 0
m = len(x)

theta0 = 0
theta1 = 0
theta2 = 0

while True:
    cnt += 1

    for i in range(m):
        diff[0] = (theta0 * x[i][0] + theta1 * x[i][1] + theta2 * x[i][2]) - y[i]
        theta0 -= alpha * diff[0] * x[i][0]
        theta1 -= alpha * diff[0] * x[i][1]
        theta2 -= alpha * diff[0] * x[i][2]

    error1 = 0
    for lp in range(len(x)):
        error1 += (y[lp] - (theta0 + theta1 * x[lp][1] + theta2 * x[lp][2])) ** 2 / 2
    if abs(error1 - error0) < epsilon:
        break
    else:
        error0 = error1

print('theta0 : %f, theta1 : %f, theta2 : %f, error1 : %f' % (theta0, theta1, theta2, error1))
print('Done: theta0 : %f, theta1 : %f, theta2 : %f' % (theta0, theta1, theta2))
print('迭代次数: %d' % cnt)

结果：

theta0 : 0.100684, theta1 : 1.564907, theta2 : 1.920652, error1 : 0.569459
Done: theta0 : 0.100684, theta1 : 1.564907, theta2 : 1.920652
迭代次数: 24

Python实现反馈神经网络
程序9-3：

import numpy as np
import math
import random

def rand(a, b):#生成随机数
    return (b - a) * random.random() + a

def make_matrix(m,n,fill=0.0):#生成相对应的矩阵
    mat = []
    for i in range(m):
        mat.append([fill] * n)
    return mat

def sigmoid(x):#激活函数
    return 1.0 / (1.0 + math.exp(-x))

def sigmod_derivate(x):#激活函数的倒函数
    return x * (1 - x)

class BPNeuralNetwork:#定义BP神经网络类

    def __init__(self):
        #各层中节点的个数
        self.input_n = 0
        self.hidden_n = 0
        self.output_n = 0
        #各层中节点的数值
        self.input_cells = []
        self.hidden_cells = []
        self.output_cells = []
        #各层的权重
        self.input_weights = []
        self.output_weights = []

    def setup(self,ni,nh,no):#数据初始化
        self.input_n = ni + 1
        self.hidden_n = nh
        self.output_n = no

        self.input_cells = [1.0] * self.input_n
        self.hidden_cells = [1.0] * self.hidden_n
        self.output_cells = [1.0] * self.output_n

        self.input_weights = make_matrix(self.input_n,self.hidden_n)
        self.output_weights = make_matrix(self.hidden_n,self.output_n)

        # random activate
        for i in range(self.input_n):
            for h in range(self.hidden_n):
                self.input_weights[i][h] = rand(-0.2, 0.2)
        for h in range(self.hidden_n):
            for o in range(self.output_n):
                self.output_weights[h][o] = rand(-2.0, 2.0)

    def predict(self,inputs):#前向的计算
        for i in range(self.input_n - 1):
            self.input_cells[i] = inputs[i]

        for j in range(self.hidden_n):
            total = 0.0
            for i in range(self.input_n):
                total += self.input_cells[i] * self.input_weights[i][j]
            self.hidden_cells[j] = sigmoid(total)

        for k in range(self.output_n):
            total = 0.0
            for j in range(self.hidden_n):
                total += self.hidden_cells[j] * self.output_weights[j][k]
            self.output_cells[k] = sigmoid(total)

        return self.output_cells[:]

    def back_propagate(self,case,label,learn):

        self.predict(case)
        #计算输出层的误差
        output_deltas = [0.0] * self.output_n
        for k in range(self.output_n):
            error = label[k] - self.output_cells[k]
            output_deltas[k] = sigmod_derivate(self.output_cells[k]) * error

        #计算隐藏层的误差
        hidden_deltas = [0.0] * self.hidden_n
        for j in range(self.hidden_n):
            error = 0.0
            for k in range(self.output_n):
                error += output_deltas[k] * self.output_weights[j][k]
            hidden_deltas[j] = sigmod_derivate(self.hidden_cells[j]) * error

        #更新输出层权重
        for j in range(self.hidden_n):
            for k in range(self.output_n):
               self.output_weights[j][k] += learn * output_deltas[k] * self.hidden_cells[j]

        #更新隐藏层权重
        for i in range(self.input_n):
            for j in range(self.hidden_n):
                self.input_weights[i][j] += learn * hidden_deltas[j] * self.input_cells[i]

        error = 0
        for o in range(len(label)):
            error += 0.5 * (label[o] - self.output_cells[o]) ** 2

        return error

    def train(self,cases,labels,limit = 100,learn = 0.05):#训练函数
        for i in range(limit):
            error = 0
            for i in range(len(cases)):
                label = labels[i]
                case = cases[i]
                error += self.back_propagate(case, label, learn)
        pass

    def test(self):#测试函数
        cases = [
            [0, 0],
            [0, 1],
            [1, 0],
            [1, 1],
        ]
        labels = [[0], [1], [1], [0]]
        self.setup(2, 5, 1)
        self.train(cases, labels, 10000, 0.05)
        for case in cases:
            print(self.predict(case))

if __name__ == '__main__':
    nn = BPNeuralNetwork()
    nn.test()

结果：

[0.10161506275617728]
[0.8956560067670083]
[0.8829086849780357]
[0.10864929306973252]