文章目录
从图的某一顶点出发,按照某种搜索方法沿着图中的边对图中所有顶点访问一次,且只访问一次。
一、广度优先搜索(Breadth-First-Search,BFS)
类似于二叉树的广度优先遍历(层序遍历),先访问起始顶点v,依次访问v的各个未被访问的邻接顶点w1、w2、……、wi,再依次访问w1、w2、……、wi的所有未被访问过的邻接顶点,直到该连通分量的所有顶点都被访问过为止。若此时图中尚有顶点未被访问过,则另选一个未曾被访问过的顶点作为起始点,重复上述过程,直到图中所有顶点都被访问到为止。
在算法中,需要使用的一个基本操作是:通过某一顶点找到与之相邻的其他顶点。可以先实现图的两个基本操作:
- FirstNeighbor(G, x):求图G中顶点x的第一个邻接点,若有则返回顶点号。若x没有邻接点或图中不存在x,则返回-1。
- NextNeighbor(G, x, y):若图G中顶点y是顶点x的一个邻接顶点,返回除y之外顶点x的下一个邻接点的顶点号,若y是x的最后一个邻接点,则返回-1。
利用这两个基本操作编写一个for循环,就可以实现通过某一顶点找到于之相邻的其他顶点:
利用这两个基本操作编写一个for循环,就可以实现通过某一顶点找到于之相邻的其他顶点:
// 通过顶点x找到与之相邻的其他顶点
for(w = FirstNeighbor(G, x);w >= 0;w = NextNeighbor(G, x, w)) {
}
在二叉树的广度优先遍历(层序遍历)中,由于二叉树不存在**“回路”,搜索相邻结点时,不可能搜到已经访问过的结点。但在图中,搜索相邻的顶点时,有可能搜到已经访问过的顶点。因此需要使用一个数组visited标记各个顶点是否已经被访问过**,只需在搜索过程中检查visited数组,就可以知道当前顶点是否已经被访问过:
// 通过顶点x找到与之相邻的其他顶点
for(w = FirstNeighbor(G, x);w >= 0;w = NextNeighbor(G, x, w)) {
// 检查x的所有邻接顶点是否被访问过
if(!visited[w]) { // 若当前顶点未被访问过
}
}
算法过程




伪代码
bool visited[MAX_VERTEX_NUM]; // 访问标记数组
// 图的广度优先遍历
void BFS(Graph G, int v) { // 从顶点v出发,广度优先遍历图G
queue<int> que; // 辅助队列
visit(v); // 访问起始顶点v
visited[v] = true; // 标记v已被访问
que.push(v); // 顶点v入队列
// 队列非空时,进入循环
while(!que.empty()) {
int x = que.front(); // 获取队头顶点x
que.pop(); // 队头顶点出队列
// 通过顶点x找到与之相邻的其他顶点
for(w = FirstNeighbor(G, x);w >= 0;w = NextNeighbor(G, x, w)) {
// 检查x的所有邻接顶点是否被访问过
if(!visited[w]) { // 若当前顶点未被访问过
visit(w); // 访问当前顶点
visited[w] = true; // 标记当前顶点已被访问
que.push(w); // 当前顶点入队列
}
}
}
}
存在的问题:
若图是非连通图,BFS函数只能遍历完起始顶点所在的连通分量,无法遍历完所有顶点。

需要在调用完BFS函数后,再次检查visited数组,看是否还有顶点未被访问,若尚有顶点未被访问过,则另选一个未曾被访问过的顶点作为起始点,再次调用BFS函数,直到图中所有顶点都被访问到为止。
最终伪代码:
bool visited[MAX_VERTEX_NUM]; // 访问标记数组
// 图的广度优先遍历
void BFS_traverse(Graph G) { // 对图G进行广度优先遍历
// 初始化visited数组
for(int i = 0;i < G.vexnum;i ++) {
visited[i] = false;
}
// 遍历顶点
for(int i = 0;i < G.vexnum; i ++) {
if(!visited[i]) { // 若当前顶点未被访问过
BFS(G, i); // 从当前顶点开始广度优先遍历图G
}
}
}
void BFS(Graph G, int v) { // 从顶点v出发,广度优先遍历图G
queue<int> que; // 辅助队列
visit(v); // 访问起始顶点v
visited[v] = true; // 标记v已被访问
que.push(v); // 顶点v入队列
// 队列非空时,进入循环
while(!que.empty()) {
int x = que.front(); // 获取队头顶点x
que.pop(); // 队头顶点出队列
// 通过顶点x找到与之相邻的其他顶点
for(w = FirstNeighbor(G, x);w >= 0;w = NextNeighbor(G, x, w)) {
// 检查x的所有邻接顶点是否被访问过
if(!visited[w]) { // 若当前顶点未被访问过
visit(w); // 访问当前顶点
visited[w] = true; // 标记当前顶点已被访问
que.push(w); // 当前顶点入队列
}
}
}
}
对于无向图,调用BFS函数的次数=图的连通分量数。
复杂度
空间复杂度:O(|V|)。
时间复杂度:
- 邻接矩阵:O(|V|2)。
- 邻接表:O(|V|+|E|)。
二、深度优先搜索(Depth-First-Search,DFS)
类似于树的先序遍历(深度优先遍历),首先访问图中某一起始顶点v,然后由v出发,访问与v邻接且未被访问的任一顶点w1,再访问与w1邻接且未被访问的任一顶点w2……重复上述过程。当不能再继续向下访问时,依次退回到最近被访问的顶点,若它还有邻接顶点未被访问国,则从该点开始继续上述搜索过程,直至图中所有顶点均被访问过为止。
在算法中,依然要使用FirstNeighbor(G, x)和NextNeighbor(G, x, y)来实现通过某一顶点找到与之相邻的其他顶点的基本操作。也需要使用数组visited标记各个顶点是否已经被访问过:
// 通过顶点x找到与之相邻的其他顶点
for(w = FirstNeighbor(G, x);w >= 0;w = NextNeighbor(G, x, w)) {
// 检查x的所有邻接顶点是否被访问过
if(!visited[w]) { // 若当前顶点未被访问过
}
}
算法过程




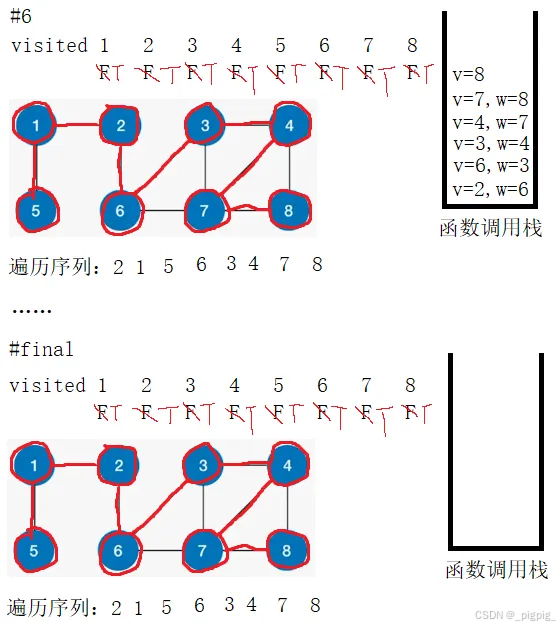
伪代码
bool visited[MAX_VERTEX_NUM]; // 访问标记数组
void DFS(Graph G, int v) { // 从顶点v出发,深度优先遍历图G
visit(v); // 访问顶点v
visited[v] = true; // 标记v已被访问
// 通过顶点v找到与之相邻的其他顶点
for(w = FirstNeighbor(G, v);w >= 0;w = NextNeighbor(G, v, w)) {
// 检查v的所有邻接顶点是否被访问过
if(!visited[w]) { // 若当前顶点未被访问过
DFS(G, w);
}
}
}
存在的问题:
若图是非连通图,DFS函数只能遍历完起始顶点所在的连通分量,无法遍历完所有顶点。

需要在调用完DFS函数后,再次检查visited数组,看是否还有顶点未被访问,若尚有顶点未被访问过,则另选一个未曾被访问过的顶点作为起始点,再次调用DFS函数,直到图中所有顶点都被访问到为止。
最终伪代码:
bool visited[MAX_VERTEX_NUM]; // 访问标记数组
// 图的深度优先遍历
void DFS_traverse(Graph G) { // 对图G进行深度优先遍历
// 初始化visited数组
for(int i = 0;i < G.vexnum;i ++) {
visited[i] = false;
}
// 遍历顶点
for(int i = 0;i < G.vexnum; i ++) {
if(!visited[i]) { // 若当前顶点未被访问过
DFS(G, i); // 从当前顶点开始深度优先遍历图G
}
}
}
void DFS(Graph G, int v) { // 从顶点v出发,深度优先遍历图G
visit(v); // 访问顶点v
visited[v] = true; // 标记v已被访问
// 通过顶点v找到与之相邻的其他顶点
for(w = FirstNeighbor(G, v);w >= 0;w = NextNeighbor(G, v, w)) {
// 检查v的所有邻接顶点是否被访问过
if(!visited[w]) { // 若当前顶点未被访问过
DFS(G, w);
}
}
}
对于无向图,调用DFS函数的次数=图的连通分量数。
复杂度
空间复杂度:O(|V|)。
时间复杂度:
- 邻接矩阵:O(|V|2)。
- 邻接表:O(|V|+|E|)。
例题

分析:在二维数组grid中,将值为’1’的元素看作是顶点,将竖向或横向的连续两个’1’看作是一条边,问题实际上就是求图grid中的连通分量的个数。遍历整个二维数组,当遇到’0’时,表示此处无顶点,或该顶点已被访问过;当遇到’1’时,表示该顶点还未被访问,从该顶点开始进行广/深度优先搜索,被访问过的顶点就将其值改为’0’表示已被访问过,直到遍历完整个二维数组,岛屿的数量就是调用广/深度优先搜索函数的次数。
广度优先搜索解法
class Solution {
public:
// 从顶点[i][j]开始广度优先搜索
void bfs(vector<vector<char>>& grid, int a ,int b) {
int m = grid.size(); // 行数
int n = grid[0].size(); // 列数
queue<pair<int, int>> que; // 定义一个辅助队列
// 访问初始顶点
grid[a][b] = '0'; // 将顶点值设为'0'表示该顶点已被访问过
que.push({a, b}); // 将初始顶点入队列
while(!que.empty()) { // 当队列不为空时进入循环
// 取出队头顶点
int i = que.front().first;
int j = que.front().second;
que.pop();
// 依次将其邻接的未被访问的顶点访问并入队列
if(i-1 >= 0 && grid[i-1][j] == '1') {
grid[i-1][j] = '0';
que.push({i-1, j});
}
if(i+1 < m && grid[i+1][j] == '1') {
grid[i+1][j] = '0';
que.push({i+1, j});
}
if(j-1 >= 0 && grid[i][j-1] == '1') {
grid[i][j-1] = '0';
que.push({i, j-1});
}
if(j+1 < n && grid[i][j+1] == '1') {
grid[i][j+1] = '0';
que.push({i, j+1});
}
}
}
int numIslands(vector<vector<char>>& grid) {
int m = grid.size(); // 行数
if(m == 0) return 0;
int n = grid[0].size(); // 列数
int count = 0; // 记录调用dfs函数的次数
// 遍历整个二维数组
for(int i = 0;i < m;i ++) {
for(int j = 0;j < n;j ++) {
// 当顶点值为'1'时表示该顶点未被访问过
if(grid[i][j] == '1') {
// 从该顶点开始广度优先地访问其所在的连通分量
bfs(grid, i, j);
count ++;
}
}
}
return count;
}
};
深度优先搜索解法
class Solution {
public:
// 从顶点[i][j]开始深度优先搜索
void dfs(vector<vector<char>>& grid, int i ,int j) {
int m = grid.size(); // 行数
int n = grid[0].size(); // 列数
// 访问初始顶点
grid[i][j] = '0'; // 将顶点值设为'0'表示该顶点已被访问过
// 按照上下左右的顺序递归的调用dfs函数访问其邻接顶点
if(i-1 >= 0 && grid[i-1][j] == '1') dfs(grid, i-1, j);
if(i+1 < m && grid[i+1][j] == '1') dfs(grid, i+1, j);
if(j-1 >= 0 && grid[i][j-1] == '1') dfs(grid, i, j-1);
if(j+1 < n && grid[i][j+1] == '1') dfs(grid, i, j+1);
}
int numIslands(vector<vector<char>>& grid) {
int m = grid.size(); // 行数
if(m == 0) return 0;
int n = grid[0].size(); // 列数
int count = 0; // 记录调用dfs函数的次数
// 遍历整个二维数组
for(int i = 0;i < m;i ++) {
for(int j = 0;j < n;j ++) {
// 当顶点值为'1'时表示该顶点未被访问过
if(grid[i][j] == '1') {
// 从该顶点开始深度优先地访问其所在的连通分量
dfs(grid, i, j);
count ++;
}
}
}
return count;
}
};
代码中访问顶点四个方向的邻接顶点可以优化为使用两个数组+for循环实现:
class Solution {
public:
// 从顶点[i][j]开始深度优先搜索
void dfs(vector<vector<char>>& grid, int i ,int j) {
int m = grid.size(); // 行数
int n = grid[0].size(); // 列数
if(i < 0 || i >= m || j < 0 || j >= n || grid[i][j] == '0') return; // 出界或等于'0'
// 访问初始顶点
grid[i][j] = '0'; // 将顶点值设为'0'表示该顶点已被访问过
// 递归的调用dfs函数访问其邻接顶点
int di[4] = {0, 0, 1, -1};
int dj[4] = {1, -1, 0, 0};
for(int index = 0;index < 4;index ++) {
dfs(grid, i+di[index], j+dj[index]);
}
}
int numIslands(vector<vector<char>>& grid) {
int m = grid.size(); // 行数
if(m == 0) return 0;
int n = grid[0].size(); // 列数
int count = 0; // 记录调用dfs函数的次数
// 遍历整个二维数组
for(int i = 0;i < m;i ++) {
for(int j = 0;j < n;j ++) {
// 当顶点值为'1'时表示该顶点未被访问过
if(grid[i][j] == '1') {
// 从该顶点开始深度优先地访问其所在的连通分量
dfs(grid, i, j);
count ++;
}
}
}
return count;
}
};
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








