FP增长算法

【2021 第一组 FP增长算法】

问题描述

        寻找频繁项是数据挖掘中一个常见问题。比如上图中，输入【数据挖掘】，搜索引擎会自动显示【工具】这个词汇，{数据挖掘，词汇}是搜索引擎记录的频繁项集。{啤酒，尿布}是交易记录中的频繁项集。

支持度&置信度

        支持度和置信度可以用来量化项集的频繁程度

        支持度：数据集中出现某个项集的比例

        置信度：置信度是针对关联规则来定义，如{尿布}->{葡萄酒}的置信度为：

                       支持度{尿布，葡萄酒} / 支持度{尿布}

Apriori算法：

        在给定数据集中，找出所有满足支持度阈值的项集，很容易想到用暴力搜索来解决问题。但是暴力搜索的时间代价是难以接受的。对于有n个商品的商店，其所有商品的可能组合共有2^n - 1种。（等价于n个元素的集合共有多少个非空子集）当n为100时，这个数字就达到了1.26*10^30。 

       

        Apriori原理： 如果某个项集是频繁的， 那么它的所有子集都是频繁的。

        Apriori原理看起来似乎对于我们来说没有什么帮助，但是它的逆否命题非常有用：

         有了这个命题，可以大幅减少暴力搜索的次数。由此产生了Apriori算法：

缺点：

• 需要多次扫描数据库
• 产生大量的候选频繁集
• 时间和空间复杂度高

        从算法第3步可以看出，候选项集不一定是原始数据集中某一项的子集

        即：x为频繁项，y为频繁项，{x，y}可以组成一个候选频繁项集，但是原始数据集中不一定存在{x，y}的组合。这使得Apriori算法有大量时间浪费在无效的集合上。

FP增长算法

        FP增长算法需要根据数据集生成FP树，FP树如右图所示

       

步骤一：过滤和排序

        统计数据集中每个元素出现次数，保留频繁元素（假设次数>3），按照元素出现次数降序排序。

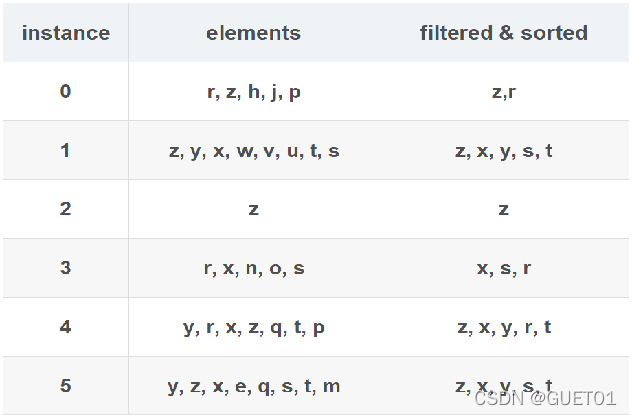
 步骤二：构造FP树

        从一个空的根结点，将步骤一过滤排序后的数据集按行依次加入树中。

        根据每一行中的元素按顺序查找结点，结点已存在时可共用结点，结点的计数需要增加。如果不存在对应结点，则创建新结点，计数为1。

 

        最终结果为： 

步骤三：在FP树中找到所有元素的前缀路径

        以r为例，r的前缀路径为：以根结点为起点，r为终点的所有路径。

        先找到FP树中所有“r”结点，然后从每一个“r”结点向根结点方向查找，找到的所有路径就是“r”的前缀路径。

        前缀路径中元素的排序是从根结点向下排序。

 

        路径后面的数字，为“r”结点上的计数，这个数字的含义表示：在原始数据集中，对应的集合与“r”共同出现的次数。

        寻找FP树中所有的“r”结点，需要遍历整棵树，这会导致算法时间复杂度较高。为了方便查找，可以用链表来加快寻找的前缀路径。将FP树中所有相同的结点用链表连接，可以将查找结点的时间复杂度从O(n)降到常数级。

        所有频繁项的前缀路径

步骤四：对每一个频繁项构造条件FP树

        以“t”为例，“t”的前缀路径为

{z，x，y，t} 2，{z，x，y，r} 1

        前缀路径可以看做是一个数据集，统计频繁元素为：

{z：3，x：3，y：3}

        类似步骤一的过滤和排序，得到：

{z，x，y}  2，{z，x，y}  1

        然后构造的FP树，是t的条件FP树

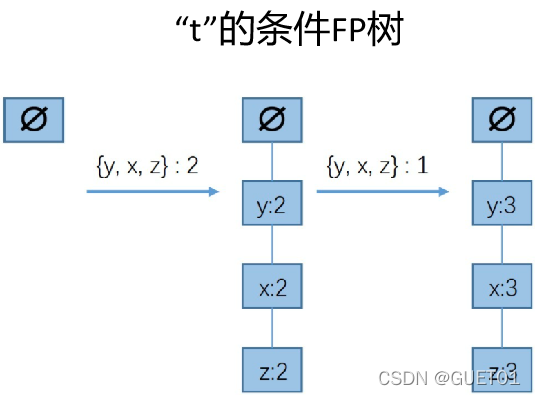
         t前缀路径中的频繁元素：{z：3，x：3，y：3}，这个数字表示：对应的元素在原始数据集中和t一起出现的次数，如{z，t}出现3次，{x，t}出现3次，{y，t}出现3次。显然，这些集合都是频繁项。

         我们也可以在t的条件FP树基础上构造x的条件FP树，对应的就是{t，x}的条件FP树。很容易发现这是一个递归的过程。

步骤五

         递归构造下一层条件FP树，直至条件FP树为空。

挖掘频繁集

        以上步骤结束之后，所有的频繁项都会有一个对应的条件FP树。对于FP增长算法很容易陷入一个误区：认为FP增长算法是通过条件FP树挖掘频繁集。

        实际上，FP树和条件FP树的作用是把遍历数据集的结果用树的结构保存下来，避免重复扫描数据集。而挖掘频繁集，是通过每一层递归中统计的频繁元素组合产生的。

        例如第一层递归中统计的频繁元素为：

z、r、x、y、s、t

        那么这些单个元素的集合：{z}，{r}，{x}...都是频繁项集。

        第二层递归，其中 t 的前缀路径中的频繁元素为：

z：3，x：3，y：3

        那么这些元素和t的组合：{t，z}，{t，x}，{t，y}也是频繁项集。

        第三层递归，{t，x} 前缀路径的频繁元素为

y：3

        所以{t，x，y}是频繁项集

......

        这些频繁项集在FP增长算法的每一层递归时同步产生，而不是算法结束后去条件FP树上去找。

附问题结果

总结

       FP增长算法和Apriori算法都利用了Apriori原理。

       共同点：找到k项频繁项集后，在其基础上找k+1项的频繁项集。

       区别：    Apriori通过k项集生成k+1项候选集，统计候选项次数。  FP增长算法生成条件FP树，根据前缀路径找k+1项的频繁项。

       FP增长算法的时间效率远远高于Apriori算法。但是由于要保存大量的条件FP树，空间效率并没有提升。

几个关键问题讨论

        1、出现次数相同的项如何排序？排序不同是否影响结果？

        无影响，但是要保证每个序列的排序相同。比如x，y出现次数相同，某个序列中x排在y前，别的序列不能出现y在x前。

        2、{x，t}的条件FP树和{t，x}的条件FP树是否相同？ 算法是否重复计算了这两个条件FP树？

        这个问题涉及到FP增长算法的一个根本问题：为什么要使用前缀路径？

        算法中找到前缀路径后，需要对前缀路径集合进行过滤和排序，获得下一层递归的数据集。那么其实使用完整的路径也可以达到目的。

        前缀路径有个非常重要的优点， 由于构造FP树之前由于对元素进行了排序，如果x出现在t的前缀路径中，那么t不可能再出现在x的前缀路径中，所以使用前缀路径避免了相同集合的重复计算！

        另外，前缀路径的查找非常方便，一个结点向根结点方向查找，只有一条路径。如果使用完整路径，结点向下查找时可能会出现分叉，处理起来会复杂很多。