概率图模型

---

1.概率图模型定义

• 概率图模型是一类用图的形式表示随机变量之间条件依赖关系的概率模型
• 图中的一个结点表示一个或者一组随机变量，结点之间边表示变量之间的概率相关关系
• 有向图称为贝叶斯网络，分为静态贝叶斯网络和动态贝叶斯网络，动态贝叶斯网络包括隐马尔科夫模型，卡尔曼滤波器
• 无向图称为马尔科夫网，包括吉布斯/波尔兹曼机 条件随机场

2. 有向概率图模型

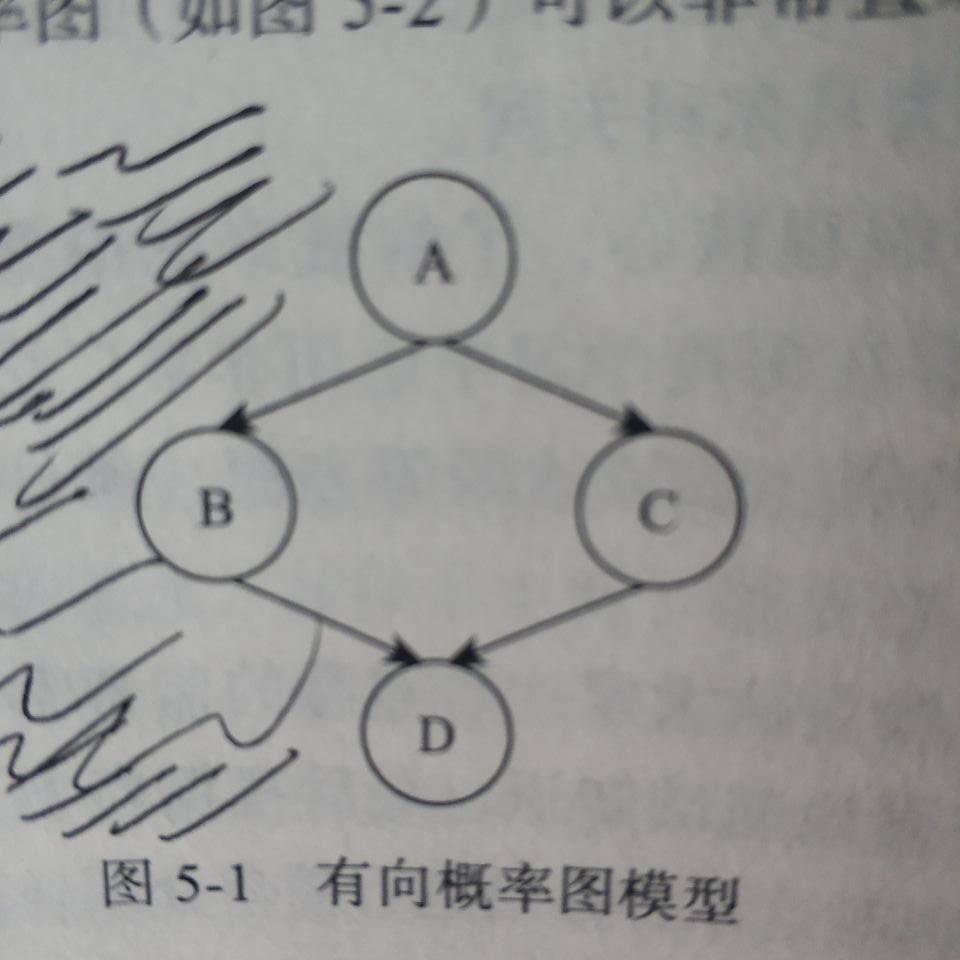
$\forall x_i\in X$都含有一个影响因子，称为父节点$g(xi)$

联合概率为$p(X)=\prod _{x_i\in X}p(xi|g(xi))$

如上图的联合概率为$P(A,B,C,D)=P(A)P(B|A)P(C|A)P(D|BC)$

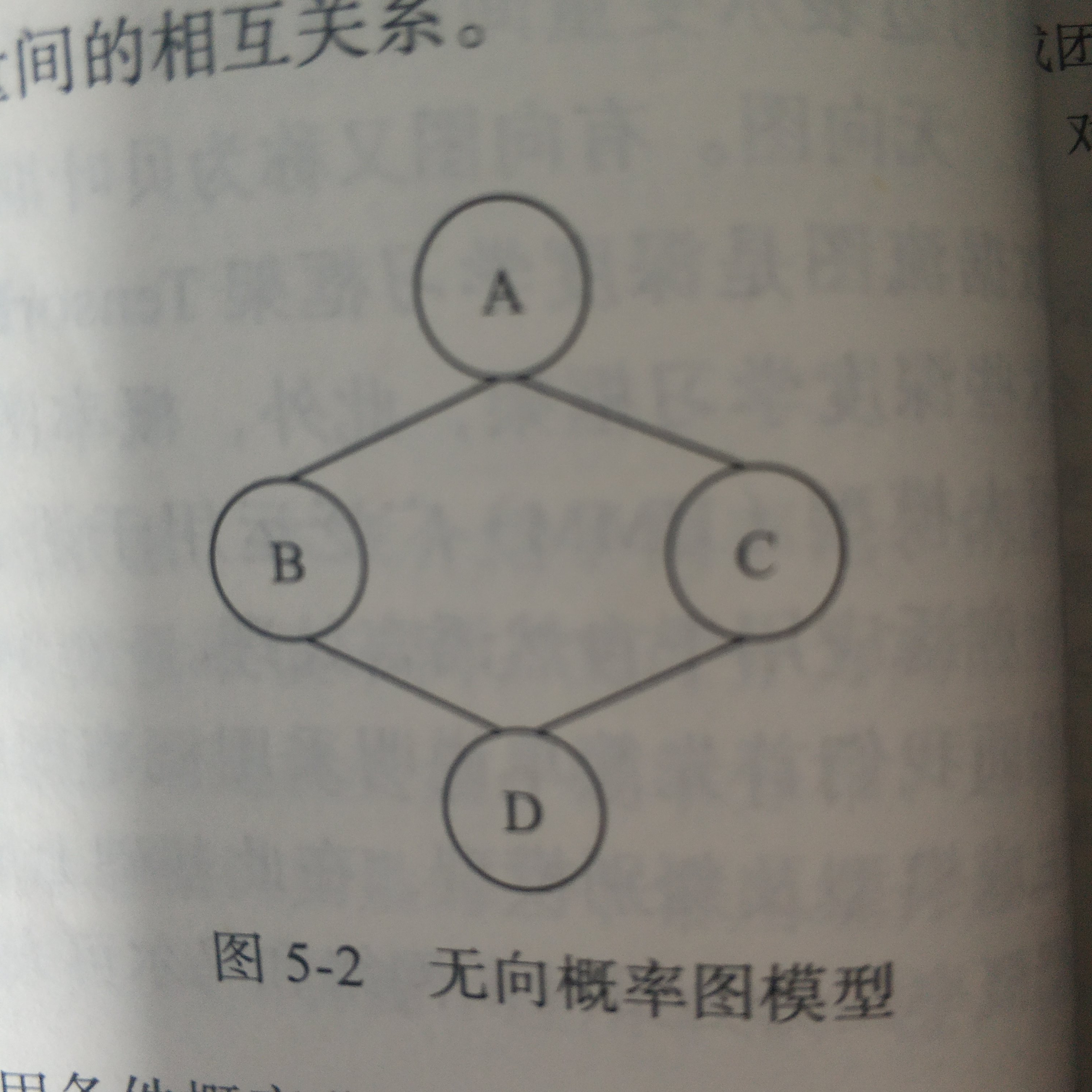
3. 无向概率图模型

1. 任意两两之间有边连接的结点集合称为团 极大团 在团中加入任意一个结点都不再形成团。

2. 无向概率图模型中每个团$C^i$都伴随着一个因子或者称为势函数，即为${\psi }^i(C^i)$, 这些因子仅仅是函数，并不是概率分布

3. 随机变量的联合概率与所有这些因子的乘积成比例，虽然不能保证乘积为1，但是可以归一化得到一个概率分布，除以常数Z使其归一化,常数通常定义为$\psi$乘积所有状态的求和或者积分$p(X)=\frac{1}{z}\prod _i{\psi }^i(C^{(i)}$

   例: $P(A,B,C,D)=\frac{1}{Z}{\psi }^1(A,B){\psi }^2(A,C){\psi }^3(B,D){\psi }^4(C,D)$

4. 有向图的联合概率可以写成各条件概率的乘积，无向图的联合概率可以写成极大团随机变量函数的乘积

4. 隐马尔科夫模型简介

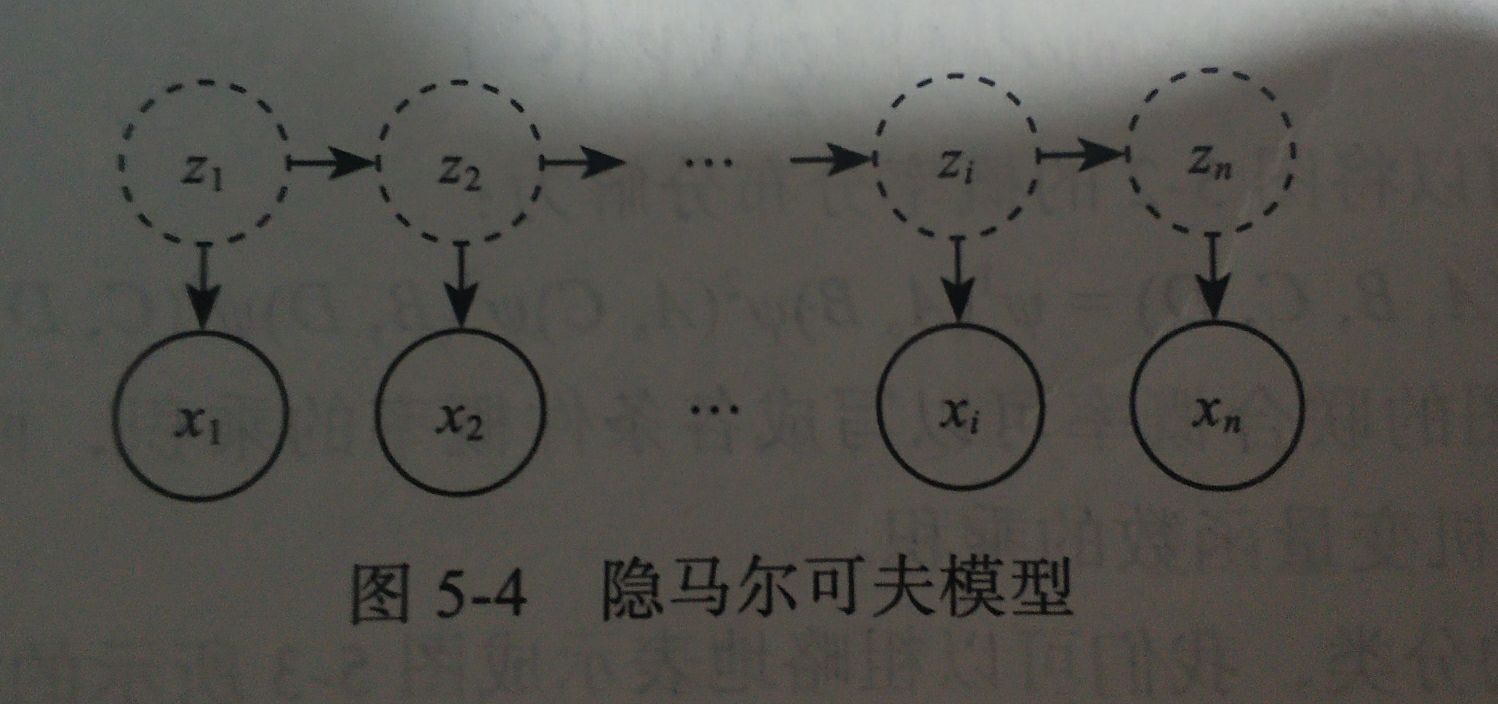
4.1 参数介绍

$->$表示状态转移 |表示观察值输出
$[z_1,z_2,z_3,z4,\cdots ,z_n]$ $z_i$表示时刻i的系统状态,通常状态变量是隐藏的，不可被观察的，此时的状态变量称为隐变量
$[x_1,x_2,x_3,x_4,\cdots ,x_n]$ $x_i$表示时刻i的系统的观察值

4.2 联合概率

$Z_{t-1}->Z_t$
|
$x_t$
横向箭头表示t时刻的状态$Z_t$仅依赖于前一个时刻t-1的状态$Z_{t-1}$与其前面的t-1的任何状态无关, $X_t$纵向箭头仅依赖于当前的状态变量,$Xt$仅由$Z_t$确定，与其他状态变量或者观察值无关，这就是所谓的马尔科夫链,所有变量的联合概率为所有条件概率的乘积(即有向图的联合概率)

$p(x_1,z_1,x_2,z_2,\cdots ,x_n,z_n)=p(z_1)p(x_1|z_1)p(z_2|z_1)p(x_2|z_2)\cdots p(z_n|z_{n-1})p(x_n|z_n)$

4.3 隐马尔科夫模型的三要素

1. 初始状态项链$(\pi =[{\pi }_1,{\pi }_2,{\pi }_3,\cdots ,{\pi }_n])$: 模型在初始时刻各状态出现的概率

   $\pi =p(z_i=s_i)i\in (1,N)$

2. 状态转移概率A : 模型在各个状态之间转移的概率.记为矩阵$A=[a_{ij}{]}_{N\times N}$

   $a_{ij}=p(z_{t+1}=s_j|z_t=s_i)i\in (1,N)$

3. 观测概率矩阵B: 模型根据当前状态获得各个观测值的概率，记为$B=[b_{ij}{]}_{N\times N}$

   $b_{ij}=p(x_t=o_j|z_t=s_i)i\in (1,N)$

4. $\pi A^n=\lambda A^n$最终$\pi$收敛在$A$的特征向量上

4.4 步骤

根据初始参数确定获取观测序列 θ = { π , A , B } \theta=\{\pi,A,B\} θ={π,A,B}

(1):根据初始状态$\pi$获取初始状态$z_1$
(2):根据状态$Z_t$和输出观测概率矩阵B选择观测变量取值$x_t$
(3):根据状态$Z_t$和状态转移矩阵A,选择确定$Z_{t+1}$
(4):若t<n,令t++,并返回第二步，否则停止

4.5 一个简单的隐马尔科夫链简单实例

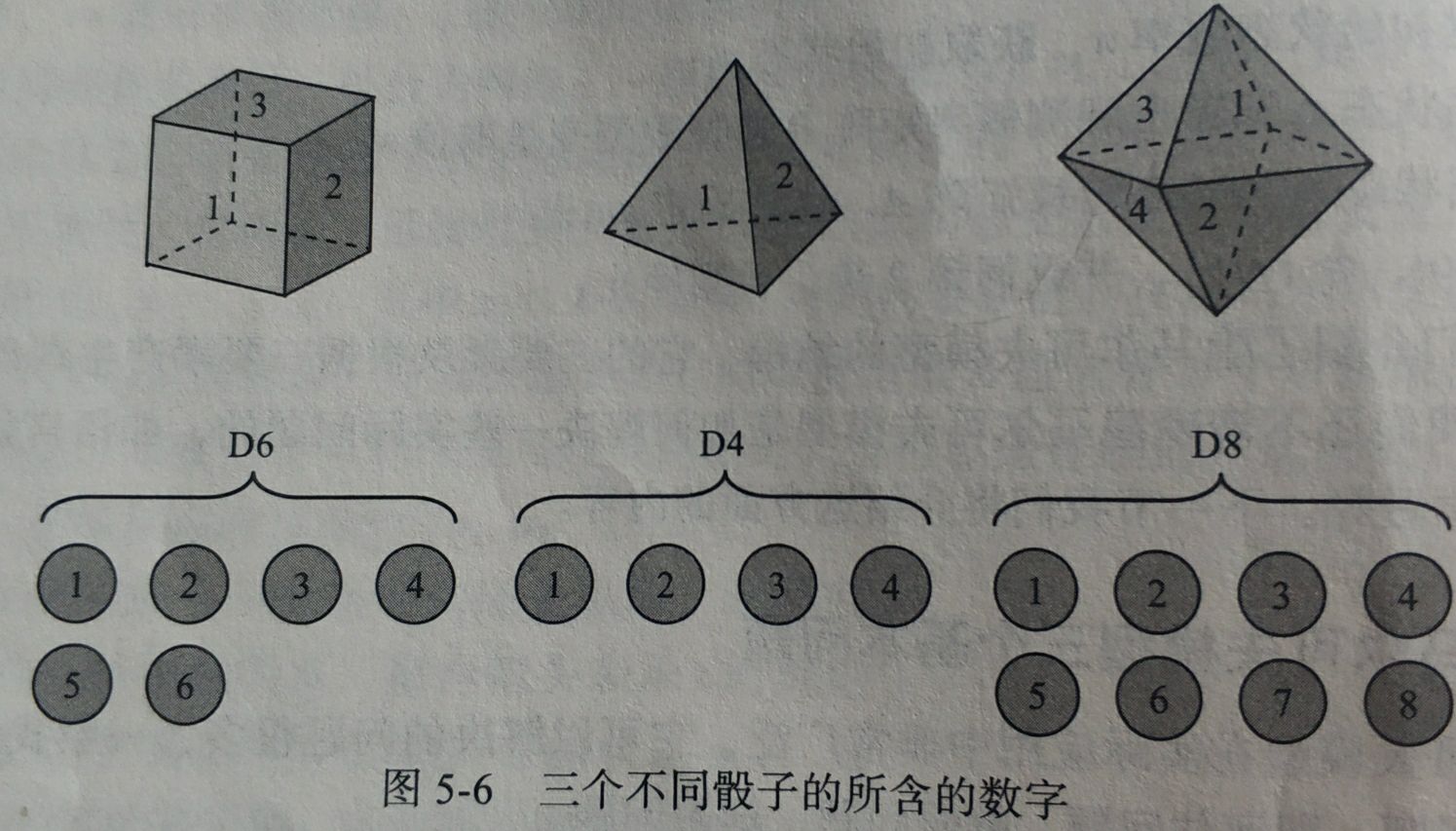
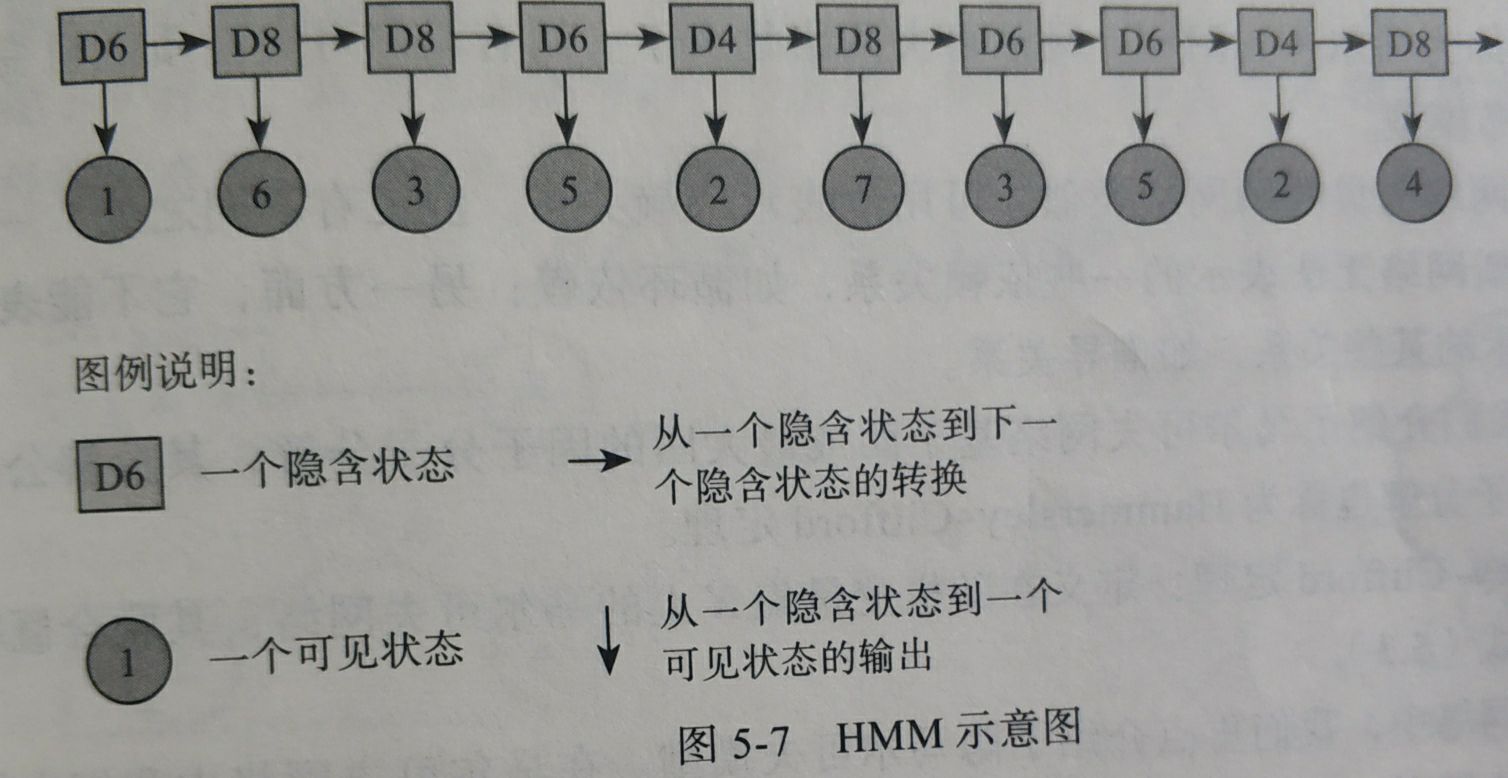
假设有三种骰子，分别由4,6,8个面
(1):每次从3个骰子中挑一个 ，获得 θ = { π , A , B } \theta=\{\pi,A,B\} θ={π,A,B}

(2):掷骰子，得到一个数字

$p(1)=p(1\cap ({\cup }_{i=1}^{n}stat{e}_i))=p(1|D_6)p(D_6)+p(1|D_4)p(D_4)+p(1|D_8)p(D_8)$

4.6 隐马尔科夫模型一般用于解决三类问题

6.1 评估问题

许多任务需要根据以往的观测序列 { x 1 , x 2 , x 3 , ⋯   , x n } \{x_1,x_2,x_3,\cdots,x_n\} {x1​,x2​,x3​,⋯,xn​}来推测当前时刻最有可能的观测值$x_n$ 这个问题可以转换为求概率$p(x|\theta )=\frac{p(x)p(\theta |x)}{p(\theta )}$
知道骰子有几种(隐含状态数量)、知道每种骰子是什么(转换概率A)、根据骰子掷出的结果(可见状态链)，了解掷出这个结果的概率
其实是检查观察到的结果和已知的模型是否吻合，如果每次结果都对应一个小的概率说明我们已知的这个模型有可能是错误的
前向算法

6.2 解码问题

给定模型{π,A,B}和观测序列 { x 1 , x 2 , x 3 , ⋯   , x n } \{x_1,x_2,x_3,\cdots,x_n\} {x1​,x2​,x3​,⋯,xn​}如何找到与之最为匹配的隐含序列 { z 1 , z 2 , z 3 , ⋯   , z n } \{z_1,z_2,z_3,\cdots,zn\} {z1​,z2​,z3​,⋯,zn}
在语音识别中观测值为语言信号，隐含状态为文字，目标就是根据观测信号来推测最有可能的隐含状态序列，也就是根据语音推测出最有可能的文字
知道骰子有几种(隐含状态数量)、知道每种骰子是什么(转换概率)、根据骰子掷出的结果(可见状态链)，推测掷出的这个结果属于哪种骰子
维比特算法

6.3 学习问题

给定观测序列 X = { x 1 , x 2 , x 3 , ⋯   , x n } X=\{x_1,x_2,x_3,\cdots,x_n\} X={x1​,x2​,x3​,⋯,xn​}如何调整参数{π,A,B}使得该序列出现的概率$p(x|\theta) $最大，这个问题就是如何根据训练样本学得最优化模型参数
Baum-Welch算法
知道骰子有几种(隐含状态数量)、知道每种骰子是什么(转换概率)、根据骰子掷出的结果(可见状态链)，反推出每种骰子是什么(转换概率)

5. 马尔科夫网络

• 一方面可以表示贝叶斯网络无法表示的一些依赖关系，如循环依赖

  另一方面不可以表示贝叶斯网络能够表示的某些关系，如推导关系

• 马尔科夫网络基于团或者最大团分解，Hammerslay-Clifford定理 联合概率$p(X)=\frac{1}{z}\prod _i{\psi }^i(C^{(i)}$

5.1 MRF 马尔科夫随机场

在概率图模型中一个重要的任务是分解概率联合函数，而函数分解通常利用随机变量的独立性或者条件独立性

设X,Y分别为两个最大团，如果X中的结点到Y中的结点都必须经过结点Z中的结点，则称结点集X和Y被结点集Z分离，Z称为分离集

5.1.1 全局马尔科夫性

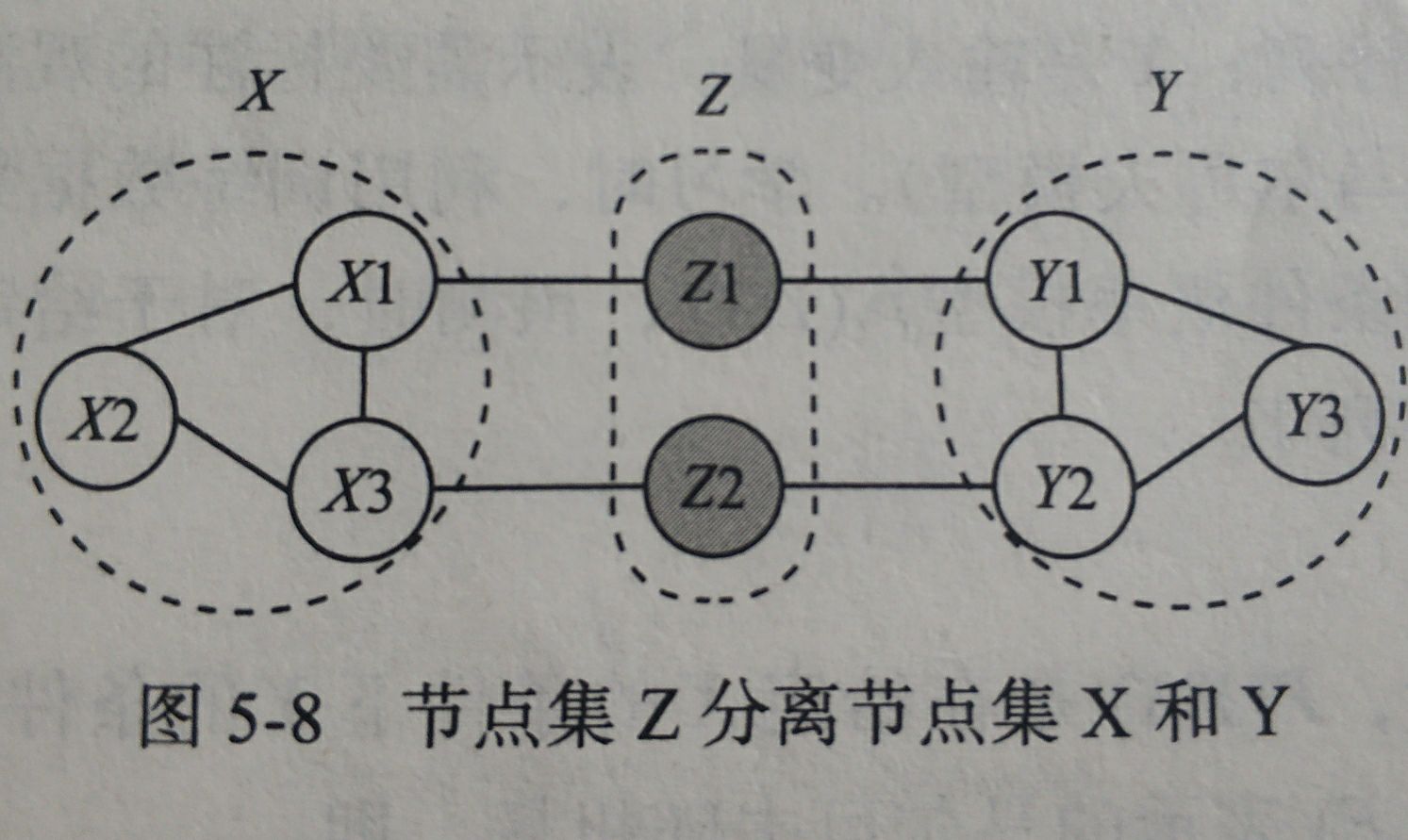
给定这两个变量子集的分离集，则两个变量子集条件独立
$P(X,Y|Z)=P(X|Z)P(Y|Z)$

5.1.2 局部马尔科夫性

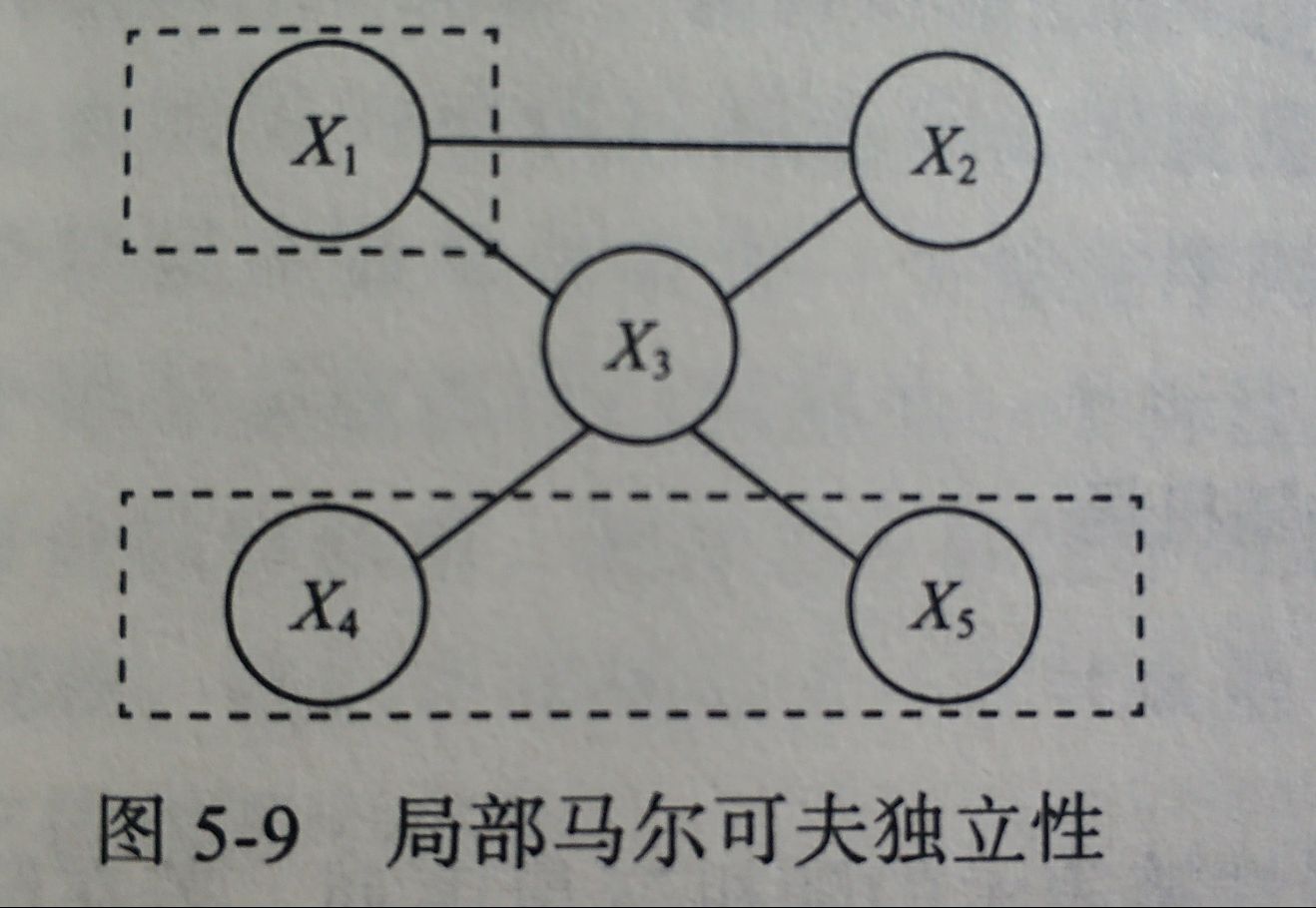
$X_1$是无向图中的一个结点， W = { X 2 , X 3 } W=\{X_2,X_3\} W={X2​,X3​}是与$ X_1$相连的所有结点，$O={X_4,X_5}$是$X_1、W$外的所有结点，则$X_1$与O独立
$P(X,O|W)=P(X|W)P(O|W)$

5.1.3 成对马尔科夫性

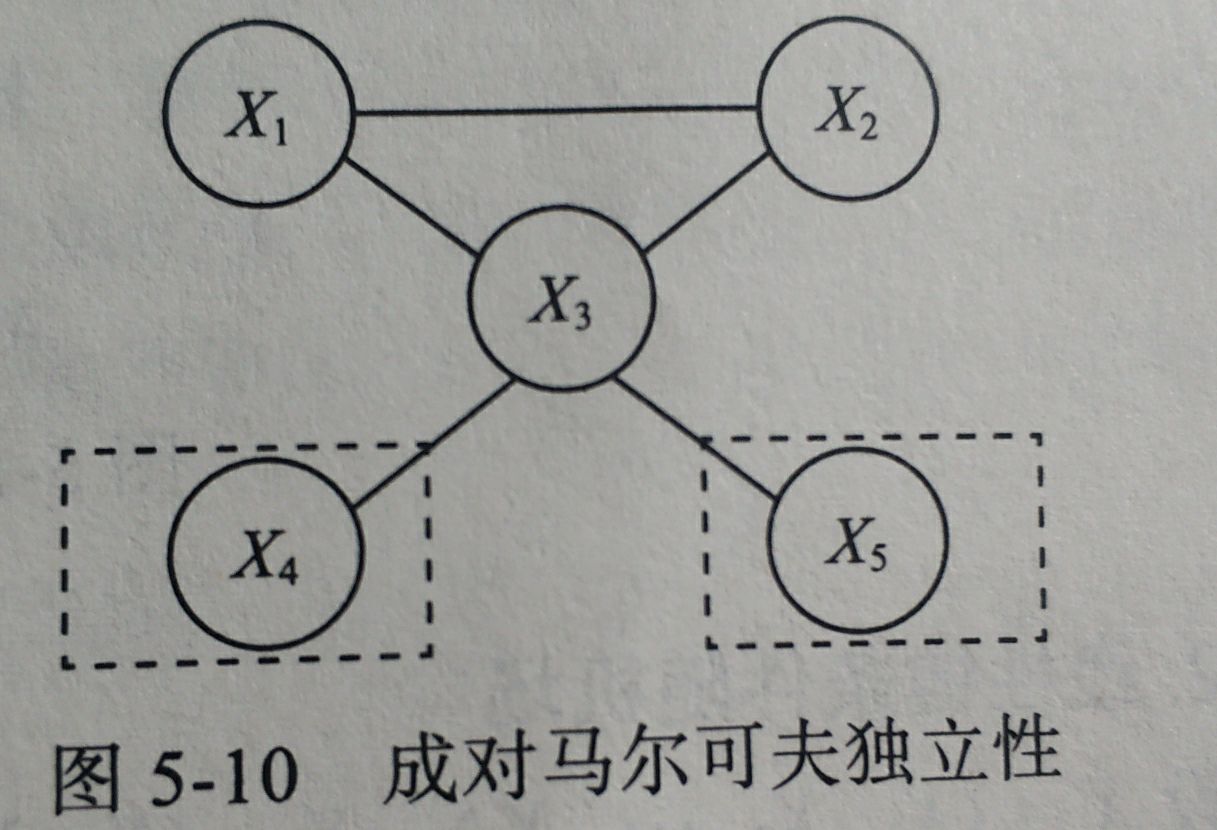
$X_4$和$X_5$是无向图中任意两个不相邻的结点，其他所有结点 O = { X 1 , X 2 , X 3 } O=\{X_1,X_2,X_3\} O={X1​,X2​,X3​}
则有$P(X_4,X_5|O)=P(X_4|O)P(X_5|O)$

5.2 CRF 条件随机场

条件随机场是条件概率分布模型$P(Y|X)$，表示的是在给定一组输入随机变量X的条件下另一组输出随机变量Y的马尔科夫随机场。CRF的特点是假设输出随机变量构成马尔科夫随机场。在$P(Y|X)$模型中，Y为输出变量，表示标记序列；X为输入变量，表示需要标注的观测序列。(可以用来进行词性标注，X为一个序列，Y为序列标注或者标记为状态序列，也就是利用X观测序列预测出来自的状态序列).训练时通过极大似然估计或者正则化的极大似然估计得到条件概率模型$\hat{P}(Y|X)$，预测时得到使$\hat{P}(Y|X)$的输出序列Y

5.2.1 条件随机场的定义

设X与Y是随机变量，$P(Y|X)$是在给定X的条件下Y的条件概率分布。若随机变量Y构成一个由无向图$G=<V,E>$表示的是马尔科夫随机场,即
$$P(Y_v|X,Y_w,w\ne v)=P(Y_v|X,Y_w,w\sim v)$$
$\forall v\in V$上述条件成立，则称$P(Y|X)$为条件随机场。

$w\ne v$表示结点v以外的所有结点，$w\sim v$表示G中与v连接的所有结点。

5.2.2 线性链条随机场

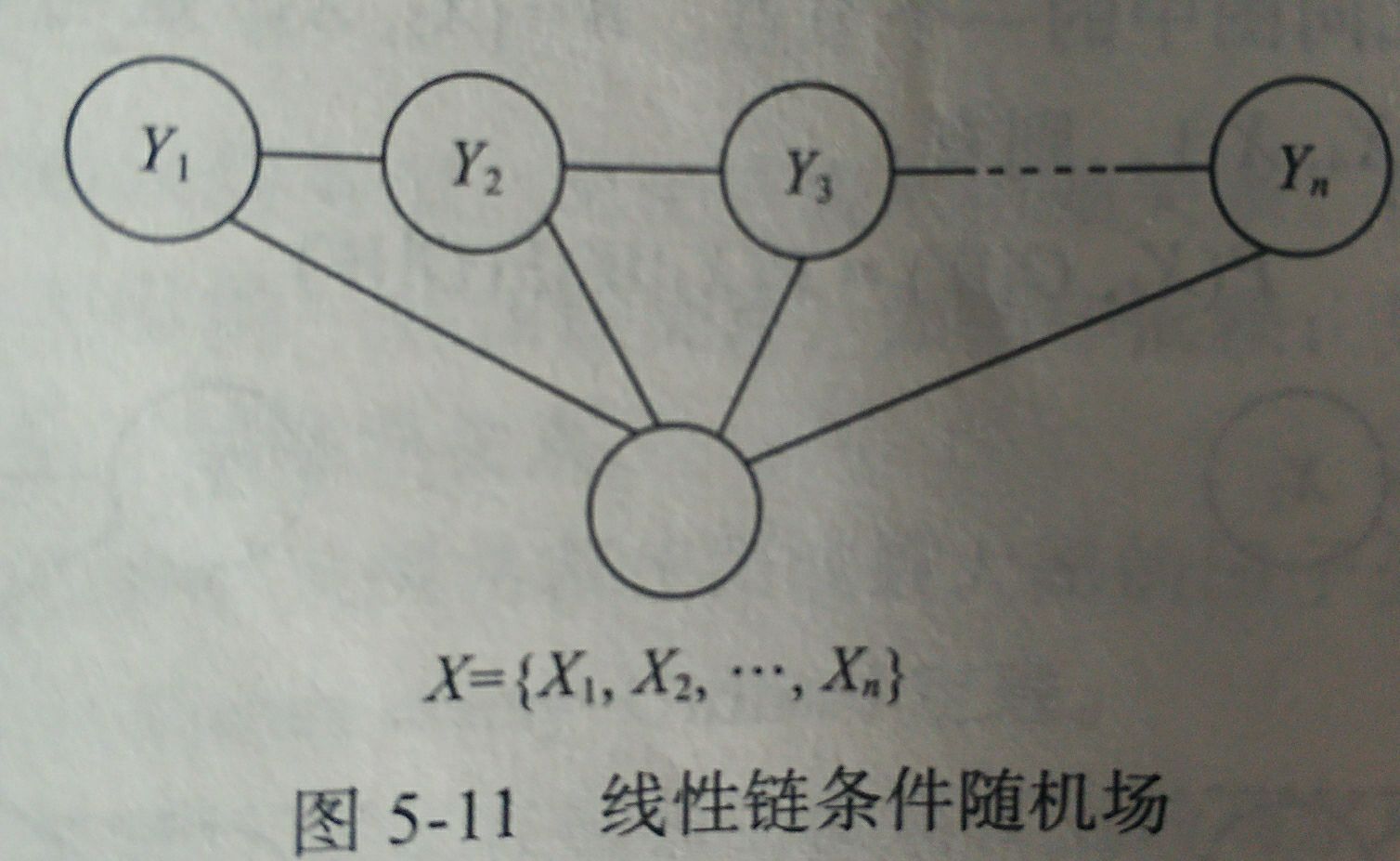
随机变量Y的条件概率分布P(Y|X)构成条件随机场，即满足马尔科夫性

$p(Y_i|X,Y_1,Y_2,\cdots ,Y_{i-1},Y_{i+1},\cdots ,Y_n)=P(Y_i|X,Y_{i-1},Y_{i+1})$

则称$P(Y|X)$为线性链条件随机场。