递归

递归

递归是程序设计语言中的一种广泛引用的算法。

递归的定义：

• 递归指函数/子程序在运行过程中直接或间接调用自身而产生的重新进入的现象，在计算机编程中，递归指的是一个过程：函数不断引用自身，直到引用的对象是已知的。

递归的优点

• 使用递归解决问题，思维清晰，而且代码少。但是在主流的高级语言中使用递归算法要耗用更多的栈空间。所以在堆栈受限时，应将量避免采用递归算法。所有的递归算法度可以改写成与之等价的非递归算法。

递归的缺点

• 递归算法解题相对常用的算法（如普通循环等），运行效率较低。
• 尽量避免使用递归算法，递归次数过多容易造成栈溢出

构成递归所必须具备的条件

• （1）子问题必须与原始问题为同样的事情，且更为简单，相对于子问题来说。
• （2）在使用递归算法时，不能无限调用本身，必须有个出口，使其化简为非递归状况处理。

递归的应用

• （1）数据的定义是按照递归定义的。（如斐波那契数列）
• （2）问题解决是按递归算法实现的。
  这类问题虽然本身没有明显的递归结构，但是递归求解比迭代求解更简单。（汉诺塔问题）
• （3）数据的结构形式是按递归定义的。（二叉树、广义表）
• 例子

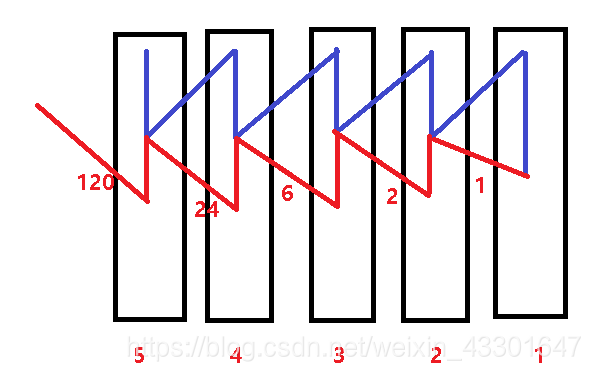
（1）求5的阶乘

public static int fac(int n){
int tmp = 1;
for(int i = 1;i <= n;i++){
tmp *=i;
}
return tmp;

//递归

public static int fac2(int n){
int tmp = 1;
if(n==1){
 tmp = 1;
 return tmp;
 }else {
        tmp = fac2(n-1)*n;
        return tmp;
    }
    }

(2)汉诺塔

public static void move(int n,char pos1,char pos2){
System.out.println(pos1+"===》"+pos2+"  ")}
public static void hanio(int n,char pos1,char pos2,char pos3) {
    if(n == 1) {
        move(pos1,pos3);
    } else {
        hanio(n-1,pos1,pos3,pos2);
        move(pos1,pos3);
        hanio(n-1,pos2,pos1,pos3);
    }
}

public static void main(String[] args) {
    hanio(1,'A','B','C');
    System.out.println();
    hanio(2,'A','B','C');
    System.out.println();
    hanio(3,'A','B','C');
}

练习题

• 1、斐波那锲数列

public static void main1(String[] args) {
     int[] Fab = new int[20];
     int i;
     Fab[0] = 1;
     Fab[1] = 1;
     for (i = 2; i < 20; i++)
         Fab[i] = Fab[i - 1] + Fab[i - 2];
     for (i = 0; i < 20; i++) {
         if (i % 5 == 0)
             System.out.println();
         System.out.printf("%6d", Fab[i]);

     }
 }

递归

public class Fab {
public static int fab(int n) {
    if (n == 0) {
        return 0;
    } else if (n == 1 || n == 2) {
        return 1;
    } else {
        return fab(n - 1) + fab(n - 2);
    }
}
    public static void main(String[] args){
        for (int i = 1; i <= 10; i++) {
            System.out.print(fab(i) + " ");

        }
    }

}

• 2、二分查找

 import  java.util.Arrays;
public class BinarySearch {
    public static int binarySearch(int[] array, int key){
    int low = 0;
    int high = array.length - 1;
    while(low <= high) {
        int mid = low + (high - low) / 2;
        if (array[mid] > key) {
            high = mid - 1;
        } else if (array[mid] >= key) {
            low = mid + 1;
        } else return mid;
    }
    return -(low+1);
}
    public static void main(String[] agrs) {
        int[] array = {1, 2, 3, 4, 5, 6};
        System.out.println(Arrays.binarySearch(array, 6));
        System.out.println(Arrays.binarySearch(array, 8));
    }
}

递归

public static int BinarySearch(int key, int[] array, int start, int end) {
    if (start > end) {
        return -1;
    }
    int mid = start + (end - start) / 2;
    if (key < array[mid]) {
        return BinarySearch(key, array, start, mid - 1);
    } else if (key > array[mid]) {
        return BinarySearch(key, array, mid + 1, end);
    } else {
        return mid;
    }
}