线性回归算法总结

线性回归原理

通常对于一组特征数据和其标记值：$(x_1,y_1)$, ($x_2$, $y_2$), …, ($x_n$, $y_n$)​，在使用特征值$x_i$​对$y_i$​进行预测时，根据习惯，如果y_i​是连续的，则称这种操作或者技术为回归；如果y_i​是离散的，则通常称为分类。
线性回归的一般形式：

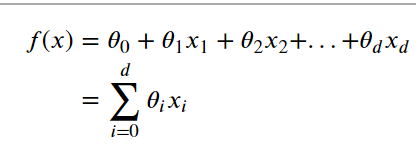
目标是找到特定的𝜃的值使f(x)尽可能接近y。均方误差是回归中常用的性能度量，即：

我们可以选择 𝜃 ，试图让均方误差最小化

极大似然估计（概率角度的诠释）

线性回归损失函数、代价函数、目标函数

损失函数(Loss Function)：度量单样本预测的错误程度，损失函数值越小，模型就越好。
代价函数(Cost Function)：度量全部样本集的平均误差。
目标函数(Object Function)：代价函数和正则化函数，最终要优化的函数。

常用的损失函数包括：0-1损失函数、平方损失函数、绝对损失函数、对数损失函数等；常用的代价函数包括均方误差、均方根误差、平均绝对误差等。

正则化

当模型复杂度增加时，有可能对训练集可以模拟的很好，但是预测测试集的效果不好，出现过拟合现象，这就出现了所谓的“结构化风险”。
结构风险最小化即为了防止过拟合而提出来的策略，定义模型复杂度为 𝐽(𝐹) ，当样本特征很多，样本数相对较少时，模型容易陷入过拟合。为了缓解过拟合问题，有两种方法：

   方法一：减少特征数量（人工选择重要特征来保留，会丢弃部分信息）。

   方法二：正则化（减少特征参数𝜃的数量级）

正则化是结构风险（损失函数+正则化项）最小化策略的体现，是在经验风险（平均损失函数）上加一个正则化项。正则化的作用就是选择经验风险和模型复杂度同时较小的模型。

防止过拟合的原理：正则化项一般是模型复杂度的单调递增函数，而经验风险负责最小化误差，使模型偏差尽可能小经验风险越小，模型越复杂，正则化项的值越大。要使正则化项也很小，那么模型复杂程度受到限制，因此就能有效地防止过拟合。
目标函数可表示为：

其中， 是用来平衡正则化项和经验风险的系数。

按正则项可分为

L_2范数正则化（Ridge Regression，岭回归）

L_1范数正则化（LASSO回归）

L_1正则项L_2正则项结合（Elastic Net）

其中，L1范数正则化、L2范数正则化都有助于降低过拟合风险。
L2范数通过对参数向量各元素平方和求平方根，使得范数最小，从而使得参数的各个元素接近0 ，但不等于0。
L1范数正则化比L2范数更易获得“稀疏”解，即范数正则化求得的会有更少的非零分量，所以范数可用于特征选择。
L2范数在参数规则化时经常用到（事实上，L0范数得到的“稀疏”解最多，但L0范数是参数中非零元素的个数，不连续，难以优化求解。因此常用L1范数来近似代替）。

优化方法

梯度下降

由于这个方法中，参数在每一个数据点上同时进行了移动，因此称为批梯度下降法，对应的，我们可以每一次让参数只针对一个数据点进行移动，即：

这个算法成为随机梯度下降法，随机梯度下降法的好处是，当数据点很多时，运行效率更高；缺点是，因为每次只针对一个样本更新参数，未必找到最快路径达到最优值，甚至有时候会出现参数在最小值附近徘徊而不是立即收敛。但当数据量很大的时候，随机梯度下降法经常优于批梯度下降法。

最小二乘法矩阵求解

线性回归评价指标

python手写代码

import numpy as np
from .metrics import r2_score

class LinearRegression:
    def __init__(self):
        '''初始化'''
        self.coef_ = None#系数
        self.interception_ = None#偏置
        self._theta = None# 系数矩阵

    def fit_normal(self,X_train,y_train):
        '''根据训练集，使用正规方程训练模型'''
        assert X_train.shape[0]==y_train.shape[0],\
            'the size of X_train must be equal to the size of y_train'
        X_b = np.hstack([np.ones((len(X_train),1)), X_train])#水平方向堆叠形成新数组，加一列1作为偏置的权重
        self._theta = np.linalg.inv(X_b.T.dot(X_b)) . dot(X_b.T) . dot(y_train)#np.linalg.inv求逆

        self.interception_ = self._theta[0]
        self.coef_ = self._theta[1:]

        return self

    def fit_gd(self,X_train,y_train,eta=0.01,n_iters=1e4,epsilon=1e-8):
        '''根据训练集，使用梯度下降法训练模型'''
        def J(theta,X_b,y):
            try:
                return np.sum((y-X_b.dot(theta))**2)/len(y)#损失函数

            except:
                return float('inf')
        def dJ(theta,X_b,y):
            return X_b.T.dot(X_b.dot(theta)-y)*2/len(X_b)
        def gradient_descent(X_b,y,initial_theta,eta=0.01,n_iters=1e4,epsilon=1e-8):
            theta = initial_theta
            i_iter = 0
            while i_iter<n_iters:
                last_theta = theta
                theta = theta - eta*dJ(theta,X_b,y)
                if abs(J(theta,X_b,y)-J(last_theta,X_b,y))<epsilon:
                    break
                i_iter+=1
            return theta

        X_b=np.hstack([np.ones((len(X_train),1)),X_train])
        initial_theta = np.zeros(X_b.shape[1])#初始化系数矩阵
        self._theta = gradient_descent(X_b,y_train,initial_theta,eta,n_iters,epsilon)
        self.interception_=self._theta[0]
        self.coef_ = self._theta[1:]
        return self

    def predict(self,X_predict):
        '''返回待预测数据集的结果向量'''
        X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
        return X_b.dot(self._theta)

    def score(self,X_test,y_test):
        y_predict=self.predict(X_test)
        return r2_score(y_test,y_predict)
    def __repr__(self):
        return 'LinearRegression()'


from sklearn import datasets
boston=datasets.load_boston()#加载波士顿房价数据集
X=boston.data#array形式
y=boston.target
X=X[y<50.0]
y=y[y<50.0]
X_train,X_test,y_train,y_test=train_test_split(X,y,seed=666)
reg=LinearRegression()
reg.fit_normal(X_train,y_train)#正规方程解,不需要归一化，公式计算
reg.coef_#系数w
reg.interception_#偏置b
reg.score(X_test,y_test)

#如果调用reg.fit_gd(X_train,y_train)
#会有警告,有溢出。这是因为使用梯度下降时没有先进行归一化
from sklearn.preprocessing import StandardScaler
standardScaler = StandardScaler()
standardScaler.fit(X_train)
X_train_standard = standardScaler.transform(X_train)
X_test_standard = standardScaler.transform(X_test)

reg=LinearRegression()
reg.fit_gd(X_train_standard,y_train)

print(reg.score(X_test_standard,y_test))

在数据量大的情况下，梯度下降法比正规方程速度快得多

sklearn封装

>>> from sklearn import linear_model
>>> reg = linear_model.LinearRegression()
>>> reg.fit ([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
>>> reg.coef_
array([ 0.5,  0.5])

>>> from sklearn import linear_model
>>> reg = linear_model.Ridge (alpha = .5)
>>> reg.fit ([[0, 0], [0, 0], [1, 1]], [0, .1, 1])
Ridge(alpha=0.5, copy_X=True, fit_intercept=True, max_iter=None,
 normalize=False, random_state=None, solver='auto', tol=0.001)
>>> reg.coef_
array([ 0.34545455,  0.34545455])
>>> reg.intercept_
0.13636...