三相分数槽绕组的设计与应用解析

分数槽绕组（q = m/p为分数）在永磁电机设计中具有多项技术优势，尤其在低速水轮发电机和永磁同步电机中表现显著。以下是其核心优势的详细分析：

1.1减少平均每极槽数

分数槽绕组通过将每对极下的槽数设计为分数，显著降低了电机的槽数与极数比例。这种设计简化了电机结构，降低了制造复杂度，同时保持了电磁性能的均衡性。

1.2改善反电势波形正弦性

通过调整绕组的短距或长距配置，分数槽技术增强了绕组的分布效应。这种优化有效抑制了反电势中的高次谐波，使得波形更接近理想正弦波，从而提升电机运行平稳性和效率。

1.3实现集中绕组设计（y=1）

分数槽绕组允许采用线圈节距y=1的集中绕组方案。这种设计缩短了端部绕组长度，减少铜耗，提高功率密度。集中绕组还简化了制造工艺，特别适合大批量生产。

1.4适配自动化绕线设备

分数槽集中绕组的对称性和规律性使其易于与专用绕线机配合。自动化绕线不仅提高生产效率，还能保证绕组的一致性，降低人工操作误差。

1.5提升整体电机性能

采用分数槽设计的电机通常表现出更高的转矩密度和更低的转矩波动。优化后的磁路分布减少了铁损和铜损，提高了电机的效率和动态响应能力。

1.6抑制齿槽转矩效应

分数槽绕组的齿槽转矩频率较高，但幅值通常小于整数槽绕组。这是由于分数槽分布破坏了磁阻变化的周期性，从而削弱了齿槽转矩的峰值，有利于低速平稳运行和精准控制。

1.7齿槽转矩次数公式

齿槽转矩次数计算公式：

N = {LCM}(Z, 2p)

其中LCM表示最小公倍数，Z为总槽数，2p为极数。分数槽设计通过增加N的次数，分散了转矩波动能量。

1.8代码示例（齿槽转矩分析）
import math

def calculate_cogging_frequency(Z, p):
    return math.lcm(Z, 2 * p)

# 示例：36槽48极分数槽设计
Z = 36
p = 8
print(f"齿槽转矩次数: {calculate_cogging_frequency(Z, p)}")
该代码输出结果为144，表明每转产生144次齿槽转矩波动，高频小幅特性显著。

2.分数槽集中绕组设计分析

2.1分数槽集中绕组的设计条件

分数槽集中绕组的设计依赖于特定的极槽配合（极对数与槽数的组合）。并非所有极槽配合都适用，需满足以下条件：
单元电机原理：分数槽绕组通常基于单元电机结构，即整个电机由多个相同的单元电机组成。每个单元电机的绕组连接方式一致。
最大公约数约束：对于分数槽电机，总槽数 ( Z ) 和极对数 ( p ) 的最大公约数为 ( t )，即 gcd(Z, p) = t )。

2.2整数槽与分数槽单元电机的区别

2.2.1整数槽电机

每极每相槽数 ( q ) 为整数

2.2.2分数槽电机

单元电机的极对数 p和槽数 Z由最大公约数决定。
每极每相槽数 q 为分数

2.3典型分数槽集中绕组的极槽配合

以下是一些常见的适用分数槽集中绕组的极槽组合（以三相电机为例）：

2.3.1 8极9槽

特点：绕组系数较高，适合小型电机设计，能够有效减少转矩波动。
应用场景：小型伺服电机、无人机电机。

2.3.2 10极12槽

特点：平衡了电磁性能和制造复杂度，齿槽转矩较低。
应用场景：电动工具、家用电器电机。

2.3.3 14极15槽

特点：绕组分布均匀，谐波含量低，适合高效率电机设计。
应用场景：工业驱动电机、电动汽车驱动系统。

2.4设计分析步骤

2.4.1验证极槽配合可行性

计算 ( gcd(Z, p) )。若为1，可直接作为单元电机；若大于1，需分解为多个单元电机。

2.4.2绕组对称性检查

分数槽绕组的每相槽数必须均等。通过电角度分布验证对称性，确保各相绕组在空间上间隔 ( 120度) 电角度。

2.4.3绕组因数计算：

分数槽绕组的分布因数 k和短距因数 k_p )需重新计算。

2.4.4注意事项

谐波抑制：分数槽绕组可能引入低次空间谐波，需通过斜极或分段设计优化。
磁动势波形：分数槽的磁动势谐波含量较高，可能影响电机噪声和转矩脉动。

3.分数槽电机单元电机参数选择约束条件

分数槽电机设计中，定子槽数 ( Z ) 和极对数 ( p ) 的组合需满足特定约束条件，以确保电机性能与对称性。以下是关键约束条件分析：

3.1相绕组对称性条件

每相绕组必须分配到相同的槽数，即： [ Z / m = 整数 ] 对于三相电机 (( m = 3 ))，( Z ) 必须为 3 的倍数，例如 ( Z = 3, 6, 9, 12, 15 ) 等。

3.2极对数选择限制

因 ( Z / p ) 为不可约分数，对于三相电机，( p ) 不能为 3 的倍数（如 3、6、9 等）。例如，( p ) 可选 1、2、4、5、7、8 等。

3.3槽数奇偶性与极对数的关系

( Z ) 为偶数时：( Z / p ) 为不可约分数，故 ( p ) 必须为奇数。例如 ( Z = 6 )，( p ) 可选 1、5、7 等。
( Z ) 为奇数时：( p ) 可为奇数或偶数。例如 ( Z = 9 )，( p ) 可选 2、4、5、7、8 等。

3.4典型参数组合示例

以下为满足条件的三相电机参数组合：
( Z = 3 )：( p = 1, 2, 4, 5, 7, ... )
( Z = 6 )：( p = 1, 5, 7, 11, 13, ... )
( Z = 9 )：( p = 2, 4, 5, 7, 8, 10, ... )
( Z = 12 )：( p = 1, 5, 7, 11, 13, 17, ... )

3.5设计注意事项

避免选择 ( p ) 为相数倍数
偶数槽时极对数需为奇数，奇数槽时极对数无奇偶限制。
实际设计中需结合电机性能目标（如转矩波动、谐波抑制）进一步优化参数。

4.开始分数槽集中绕组设计（10极12槽）

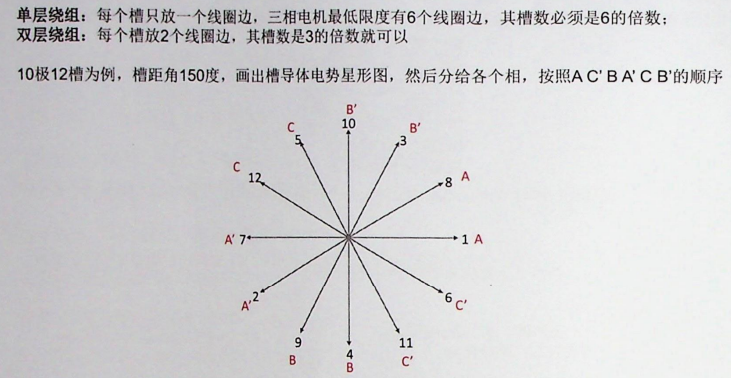
分数槽集中绕组的设计需要考虑槽数、极数以及绕组排列方式。以10极12槽为例，槽距角和电势星形图的绘制步骤如下。

4.1槽距角计算

槽距角（α）是指相邻槽之间的电角度，计算公式为：180*p/Q 其中，( p )为极对数，( Q )为槽数。对于10极12槽电机： [ p = 5 ] [ Q = 12 ] 180*5/12因此，每个槽的电角度间隔为75度。

4.2电势星形图绘制

电势星形图表示各槽导体感应电势的相位关系。12个槽的电势星形图绘制如下：
将12个槽的电势相位按75度间隔排列在圆周上。
槽1电势相位为0度，槽2为75度，槽3为150度，依此类推，槽12为825度（实际等同于165度，因为360度为一周期）。
电势星形图显示出12个电势相量，相邻相量间隔75度。

4.3相带分配

对于三相绕组，按照ACBACB的顺序分配相带：

4.3.1 A相

选择电势星形图中相位接近0度的槽。例如槽1（0度）、槽2（75度）、槽7（375度，等效为15度）、槽8（450度，等效为90度）。

4.3.2 C相

选择相位接近120度的槽。例如槽3（150度）、槽4（225度）、槽9（525度，等效为165度）、槽10（600度，等效为240度）。

4.3.3 B相

选择相位接近240度的槽。例如槽5（300度）、槽6（375度，等效为15度）、槽11（750度，等效为30度）、槽12（825度，等效为165度）。
实际分配时需根据具体绕组设计调整槽的归属，确保三相平衡。

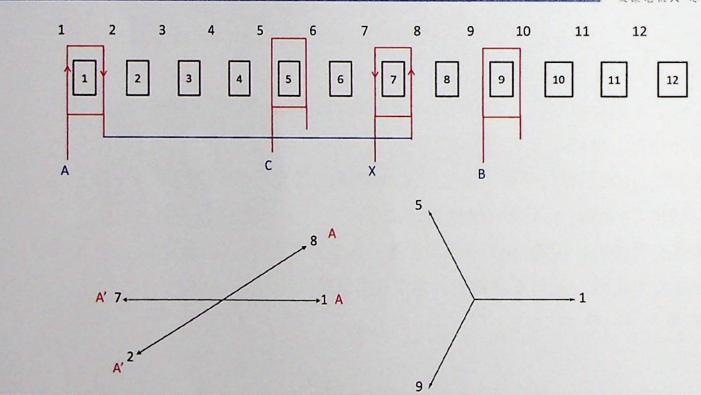
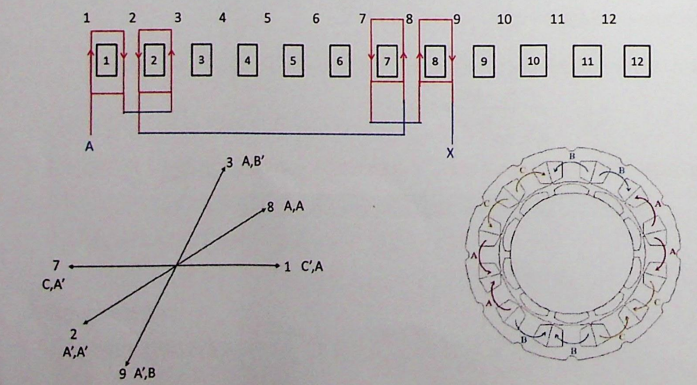
4.4绕组排列示例

以双层绕组为例，每个槽包含两个线圈边，上层和下层：
A相：上层线圈边选择槽1、槽2、槽7、槽8，下层线圈边根据跨距选择对应槽。
C相：上层线圈边选择槽3、槽4、槽9、槽10，下层线圈边根据跨距选择对应槽。
B相：上层线圈边选择槽5、槽6、槽11、槽12，下层线圈边根据跨距选择对应槽。
线圈跨距通常选择为极距的整数倍，极距计算为：Q/2p= 1.2 ] 取整后跨距为1槽。

4.5注意事项

分数槽绕组设计需确保：
三相电势对称，避免谐波过大。
绕组系数计算需考虑槽距角和短距效应。
实际应用中需结合电机具体参数优化设计。

5.计算分布系数和短距系数

5.1分布系数（Distribution Factor）

分布系数用于描述交流电机绕组中，由于线圈分布在不同的槽中，导致感应电动势在相位上存在差异，从而使得合成电动势小于各线圈电动势的算术和。分布系数反映了线圈分布对合成电动势的影响。
计算公式为： [ K_d = \frac{\sin\left(\frac{q \alpha}{2}\right)}{q \sin\left(\frac{\alpha}{2}\right)} ] 其中：
( q ) 为每极每相槽数
( \alpha ) 为槽距角，即相邻槽之间的电角度，( \alpha = \frac{180^\circ}{\text{每极槽数}} )
分布系数通常小于1，表明分布绕组会减小合成电动势。

5.2短距系数（Pitch Factor）

短距系数用于描述当线圈的节距（跨距）小于极距时，线圈两边的感应电动势相位差不是180度，导致合成电动势小于全距绕组时的值。短距系数反映了线圈节距对电动势的影响。
计算公式为： [ K_p = \cos\left(\frac{\beta}{2}\right) ] 其中：
( \beta ) 为短距角，即线圈节距与极距的电角度之差。若极距为 ( \tau )，线圈节距为 ( y )，则 ( \beta = 180^\circ \times \left(1 - \frac{y}{\tau}\right) )
短距系数通常也小于1，表明短距绕组会减小合成电动势。

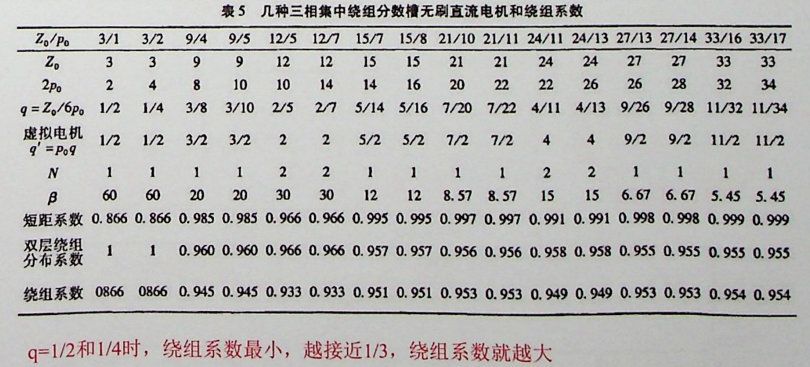
5.3绕组系数（Winding Factor）

分布系数和短距系数共同决定了绕组的有效电动势，两者的乘积称为绕组系数： [ K_w = K_d \times K_p ] 绕组系数综合反映了分布和短距对合成电动势的影响，其值小于或等于1。