蓝桥杯培训1

例题1 数字三角形问题
有一个由非负整数组成的三角形，第一行只有一个数，除了最下行之外每个数的左下方和右下方各有一个数，如下图所示：

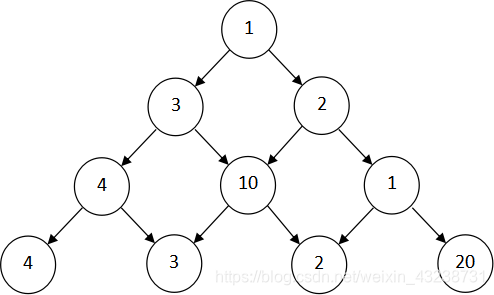
从第一行的数开始，每次可以往左下或右下走一格，直到走到最下行，把沿途经过的数全部加起来，如何走才能使得这个和最大？
分析：
这是一个动态的决策问题：每次有两种选择，是可以用回溯法求出所有路线，再从中选取最优，但是效率太低，一个n层的数字三角形的完整路线有2n-1条。
用状态和状态转移的思路：把当前位置(i , j)看成一个状态，然后定义状态(i , j)的指标函数d(i , j)——从格子(i , j)出发时能得到的最大和(包括当前格子本身的值)。这样理解，原问题就变成求解d(1 , 1)。

从(i , j)出发，要么是(i+1 , j)，要么是(i+1 , j+1)，所以得到如下状态转移方程：
d(i , j) = a(i , j) + max{ d(i+1 , j) , d(i+1 , j+1) }  其中，a(i , j)为当前节点的值。
这个性质称为最优子结构(optimal substructure)，或者描述为“全局最优解包含局部最优解”。

方法1：递归计算
int solve(int i , int j) {
return a[i][j] + ( i == n ? 0 : max(solve(i+1 , j) , solve(i+1, j+1)));
}
正确但效率低，有重复计算的问题。比如solve(2,1)时计算了一次solve(3,2)，而计算solve(2,2)时又计算了一次solve(3,2)。n层的三角形，一共算了2n-1个结点，时间复杂度为O(2n)。
方法2：递推计算
int i , j;
for( j=1 ; j<=n ; j++)
d[n][j] = a[n][j];
for( i=n-1 ; i>=1 ; i–)
for( j=1 ; j<=i ; j++)
d[i][j] = a[i][j] + max( d[i+1][j] , d[i+1][j+1] );
递推方法之所以这样，是因为i为逆序枚举的，因此在计算d[i][j]之前，必须先把d(i+1 , j)和d(i+1 , j+1)计算出来。此法的时间复杂度降低到O(n2)。
方法3：记忆化搜索
首先用语句“memset(d , -1 , sizeof(d))”(Java中可以用Arrays.fill(d , -1))，把数组d全部初始化为-1，然后编写改进的递归函数：
int solve(int i , int j) {
if(d[i][j] >= 0) return d[i][j];
return d[i][j] = a[i][j] + ( i == n ? 0 : max(solve(i+1 , j) , solve(i+1, j+1))); //赋值语句本身有返回值，所以赋值与return合并
}
上述程序用初始化的-1指示接点未计算，如果d[i][j] >= 0则表示它已被计算过，直接返回d[i][j]值。改进后，该方法计算的结点数就是原本三角形里的结点数，即n*(n+1) / 2，时间复杂度降为O(n2)。

完成过程：
1.可能因为DEV的本身软件问题，在开始做的时候出现没法定义二维数组的情况。。。删了好多语句才找到这个，真的无语。
2.原理真的很简单，第一个方法复杂了点，每次挑选下一行结点中较大的。第二个方法冲下往上堆数值，左右中挑大的堆，直到根（根节点？就看作是吧）节点。

代码：
#include <stdio.h>
#include <math.h>
#define MAXSIZE 100
int a[MAXSIZE][MAXSIZE],row;
int max(int a,int b)
{
return a>b?a:b;
}
int solve(int i,int j)
{
return a[i][j]+(irow?0:max(solve(i+1,j),solve(i+1,j+1)));
}
int main()
{
FILE *f1,*f2;
int n,x,i,j,ans;
f1=fopen(“count.in”,“r”);
f2=fopen(“Count.out”,“w”);
if(f1NULL)
{
printf(“This file does not exist!!!”);
}
fscanf(f1,"%d",&row);
n=((int)pow(2,row))-1;
for(i=0;i<row;i++)
{
for(j=0;j<=i;j++)
{
fscanf(f1,"%d",&a[i][j]);
}
}
ans=solve(0,0);
printf("%d",ans);
fclose(f1);
fclose(f2);
}