高斯消元：列主消元法

什么是列主消元

（注： akk代表第k行第k列的权值， 以下摘自百度百科：列主消元法）
列主元素消去法是为控制舍入误差而提出来的一种算法，列主元素消去法计算基本上能控制舍入误差的影响，其基本思想是：在进行第 k(k=1,2,…,n-1)步消元时，从第k列的 akk及其以下的各元素中选取绝对值最大的元素，然后通过行变换将它交换到主元素akk的位置上，再进行消元。
BZ：好吧！其实思路的挺清晰的，那么，我们就开始放代码了：：：

//#include<bits/stdc++.h>
#include<stdio.h>
#include<iostream>
#include<algorithm>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#include<stack>
#include<queue>			//stack的头文件
using namespace std ;
typedef long long ll;
#define MAXN 501
#define INF 0x3f3f3f3f
#define MALL (BiTnode *)malloc(sizeof(BiTnode));

double a[MAXN][MAXN+1];
double b[MAXN][MAXN+1];
double x[MAXN];
void init(int n)                            //输入n阶矩阵,包含输入增广矩阵，即[n*(n-1)]
{
    memset(a, 0, sizeof(a));
    for(int i=1; i<=n; ++i)
        for(int j=1; j<=n+1; ++j)
        {
            scanf("%lf", &a[i][j]);
            b[i][j] = a[i][j];
        }
}

int gaosi(int n)
{
    for(int i=1; i<n; ++i)
    {
        if(!b[i][i])
            return 0;
        for(int j=i+1; j<=n+1; ++j)
        {
            double ans = 1.0*b[j][i]/b[i][i];
            for(int k=i; k<=n+1; ++k)
                b[j][k] = b[j][k] - 1.0*ans*b[i][k];
        }
    }
     if(!b[n][n])
        return 0;
    return 1;
}

int gaosi_liezhu(int n)                      //列主消元（上三角）
{
    for(int i=1; i<n; ++i)
    {
        double tem = fabs(a[i][i]);          //tem标记第i行第i列以下第x(x >= i)列中的绝对值最大的数
        int cnt = i;                         //cnt标记第几行，用于行交换。

        for(int j=i+1; j<=n; ++j)
        {
            if(fabs(a[j][i]) > tem)
            {
                tem = fabs(a[j][i]);
                cnt = j;
            }
        }
        for(int j=i; j<=n+1; ++j)           //行交换
        {
            double p = a[i][j];
            a[i][j] = a[cnt][j];
            a[cnt][j] = p;
        }

        if(!a[i][i])                        //正常的高斯消元
            return 0;
        for(int j=i+1; j<=n; ++j)
        {
            double ans = 1.0*a[j][i]/a[i][i];
            for(int k=i; k<=n+1; ++k)
                a[j][k] = a[j][k] - 1.0*ans*a[i][k];
        }
    }
     if(!a[n][n])
        return 0;
    return 1;
}

void print_a(int n)           //输出消元后的上三角矩阵
{
    for(int i=1; i<=n; ++i)
    {
        for(int j=1; j<=n+1; ++j)
            if(a[i][j] < 1e-5 && a[i][j] > -1e-5)
                printf("0.0 ");
            else
                printf("%.1f ", a[i][j]);
        cout << '\n';

    }
}

void print_b(int n)           //输出消元后的上三角矩阵
{
    for(int i=1; i<=n; ++i)
    {
        for(int j=1; j<=n+1; ++j)
            if(b[i][j] < 1e-5 && b[i][j] > -1e-5)
                printf("0.0 ");
            else
                printf("%.1f ", b[i][j]);
        cout << '\n';
    }
}

void jie_a(int n)                //回代方程求出方程组的解；
{
    memset(x, 0, sizeof(x));
    x[n] = 1.0*a[n][n+1]/a[n][n];
    for(int i=n-1; i>0; --i)
    {
        double ans=0.0;
        for(int j=i+1; j<=n; ++j)
            ans+=1.0*a[i][j]*x[j];
        x[i] = (a[i][n+1] - ans)*1.0/a[i][i];
    }

    for(int i=1; i<=n; ++i)
        if(x[i] < 1e-5 && x[i] > -1e-5)
            printf("x%d = 0.0\n", i);
        else
            printf("x%d = %.1f\n", i, x[i]);
}

void jie_b(int n)                //回代方程求出方程组的解；
{
    memset(x, 0, sizeof(x));
    x[n] = 1.0*b[n][n+1]/b[n][n];
    for(int i=n-1; i>0; --i)
    {
        double ans=0.0;
        for(int j=i+1; j<=n; ++j)
            ans+=1.0*b[i][j]*x[j];
        x[i] = (b[i][n+1] - ans)*1.0/b[i][i];
    }

    for(int i=1; i<=n; ++i)
        if(x[i] < 1e-5 && x[i] > -1e-5)
            printf("x%d = 0.0\n", i);

        else
            printf("x%d = %.1f\n", i, x[i]);
}
int main()
{
    double a[MAXN][MAXN+1];
    cout << "请输入方程的阶数n：";
    int n;
    cin >> n;
    cout << "请输入n阶方程的增广矩阵：" << '\n';
    init(n);
    cout << "\n-------高斯消元后的结果为------" << '\n';
    int j = gaosi(n);
    if(j)
    {
        print_b(n);
        cout << "----利用该矩阵回代后解出其解为----" << '\n';
        jie_b(n);
    }
    else
        cout << "该方程组顺序消元后无解！" << '\n';
    cout << "\n-------列主消元后的结果为------" << '\n';
    int i = gaosi_liezhu(n);
    if(i)
    {
        print_a(n);
        cout << "----利用该矩阵回代后解出其解为----" << '\n';
        jie_a(n);
    }
    else
        cout << "该方程组列主消元后无解！" << '\n';
    return 0;
}

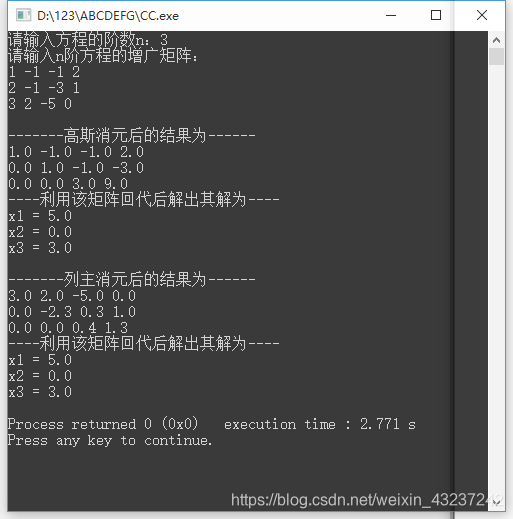
##### 样例检测：

方程组：
x1 - x2 - x3 = 2,
2 * x1 - x2 - 3 * x3 = 1,
3 * x1 + 2 * x2 - 5 * x3 = 0.