数组扩容以及优化的冒泡排序法

最新推荐文章于 2025-08-11 15:37:01 发布
最新推荐文章于 2025-08-11 15:37:01 发布
阅读量271 收藏
点赞数
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/weixin_43229819/article/details/83041738

关于数组扩容

，我们通常用到的地方可能就是关于对于数组的处理，比如对于指定的索引位置，我们需要删除这个元素，也有可能就是增加元素，那么在增加元素的过程中，原数组的大小已经固定，我们就需要对其进行扩容。
在这里我们封装一个方法，可在main中调用（实际这个方法在之前并没有进行封装处理，为了测试其他元素故进行封装处理）

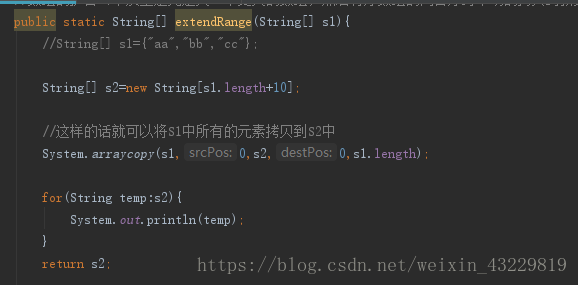
在这里插入图片描述

然后我再调用，这里我们可以看到，扩容的本质其实就是重新定义一个对象数组，在之前的length加上需要的大小
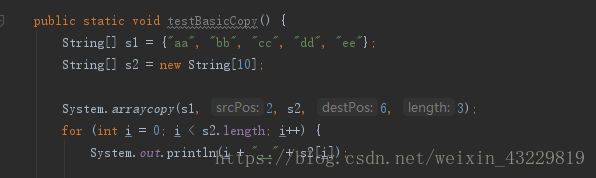
在这里插入图片描述

下面关于是冒泡排序方法

的优化处理，我们知道，冒泡方法的原理就是逐一比较大小在这里直接给出代码，进行解释
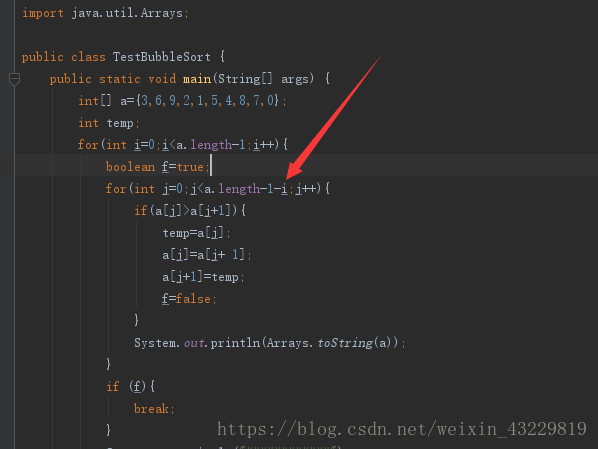
在这里插入图片描述
在这里，我们看到是j<a,lengthj-1-i,那么为什么减去i，原因是因为我们可以省略重复的比较步骤，比如说，在算法的某一步我们已经得到2，1，0，4，5，6，但是由于算法的问题这一个步骤会重复处理，我们在之前的for循环定义的i减去之后便可以省略。

另外还有一个优化的问题就是在这行代码的前面，我们定义了一个boolean类型的变量f，这个和为什么减去i类似，不过解释起来更容易，比如说我们已经将0123456排序好但是这是i并没有到最大值，由于算法的问题，计算机仍然需要将i的值处理到i<a.length-1为止，我们定义的这个boolean类型的f，原理是如果检测到有进行交换，那么此时f的值为false，如果检测到f的值为true，也就是没有交换，那么我们就break，结束循环推出。

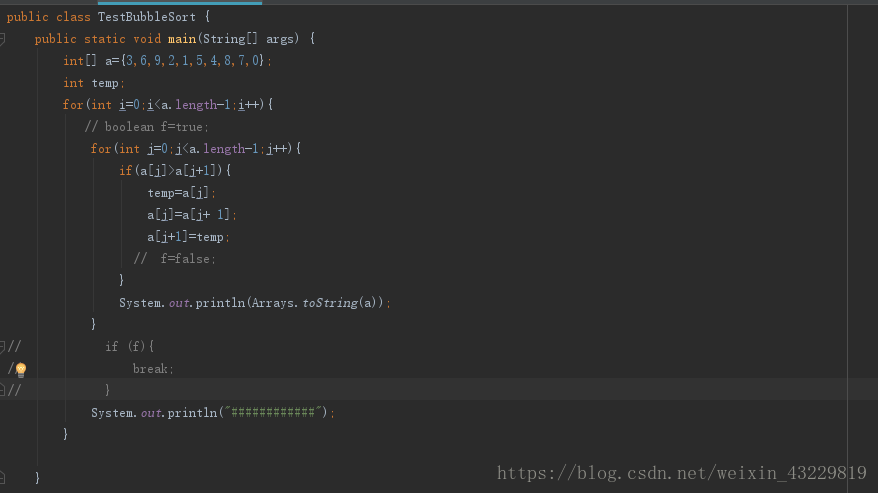
关于这两个方面的优化，解释的有不到位的地方请谅解，大家尽量手动敲敲代码试试看，随机定义一个数组，然后将代码这样写进行一下比较就能体会到了。下面为测试没有优化的冒泡排序法的代码

在这里插入图片描述

数组 排序
pythontxt的博客
04-28 1003
数组6
韩顺平零基础Java(超详细笔记梳理) 05——数组（语法，赋值机制，拷贝反转）、排序（冒泡排序）、查找、二维数组（杨辉三角）
apple_68589597的博客
07-18 1264
本篇文章是韩顺平老师课程P156-P189（第六章：数组排序和查找）重点内容的详细总结，内容包括：数组（语法、赋值机制、反转、扩容）；排序（冒泡）；查找；二维数组（杨辉三角）
算法之---数组动态扩容
牧码人的专栏
08-23 290
最近几天做项目，遇到些比较棘手的问题，本来是上游系统接口数据可以送正确的，但是耍无赖不给送，导致我们自己的处理。因为是外网系统接口处理数据，接收到的是xml文件，而我们程序采用xmlbean对xml进行解析，于是会出现数组的情况。 产生问题的原因为，对于存在关系的xml中，当前xml会有个组信息的节点，通常关系为两两的关系，而如何识别他们是有关系的呢，考的是一个唯一id，也就是xml1中的组信息...
Java数组扩容算法及Java对它的应用
chuqi1313的博客
09-13 130
　　Java数组扩容的原理 　　1）Java数组对象的大小是固定不变的，数组对象是不可扩容的。 　　2）利用数组复制方法可以变通的实现数组扩容。 　　3）System.arraycopy()可以复制数组。 　　4）Arrays.copyOf()可以简便的创建数组副本。 　　5）创建数...
数组的扩容
weixin_42554389的博客
08-20 341
原来的数组所占据的空间将会被垃圾回收级制（GC）回收； 数组扩容涉及数组的拷贝，数组拷贝会耗费大量的资源； 数组的优化： 创建数组的时候，预先估计数组中存储元素的个数，给定初始化容量，减少数组的拷贝，提高程序的执行效率。 ...
java基于可扩充数组的向量实现(算法源码)
01-15
/* * 基于可扩充数组的向量实现 */ package dsa; public class Vector_ExtArray implements Vector { private int N = 8;//数组的容量，可不断增加 private int n;//向量的实际规模 private Object A[];//对象数组 //构造函数 public Vector_ExtArray() { A = new Object[N]; n = 0; } //返回向量中元素数目 public int getSize() { return n; } //判断向量是否为空 public boolean isEmpty() { return (0 == n) ? true : false; } //取秩为r的元素 public Object getAtRank(int r) throws ExceptionBoundaryViolation { if (0 > r || r >= n) throw new ExceptionBoundaryViolation("意外：秩越界"); return A[r]; } //将秩为r的元素替换为obj public Object replaceAtRank(int r, Object obj) throws ExceptionBoundaryViolation { if (0 > r || r >= n) throw new ExceptionBoundaryViolation("意外：秩越界"); Object bak = A[r]; A[r] = obj; return bak; } //插入obj，作为秩为r的元素；并返回该元素 public Object insertAtRank(int r, Object obj) throws ExceptionBoundaryViolation { if (0 > r || r > n) throw new ExceptionBoundaryViolation("意外：秩越界"); if (N <= n) {//空间溢出的处理 N *= 2; Object B[] = new Object[N];//开辟一个容量加倍的数组 for (int i=0; ir; i--) A[i] = A[i-1];//后续元素顺次后移 A[r] = obj;//插入 n++;//更新当前规模 return obj; } //删除秩为r的元素 public Object removeAtRank(int r) throws ExceptionBoundaryViolation { if (0 > r || r >= n) throw new ExceptionBoundaryViolation("意外：秩越界"); Object bak = A[r]; for (int i=r; i<n-1; i++) A[i] = A[i+1];//后续元素顺次前移 n--;//更新当前规模 return bak; } }
数据结构与算法 数组的动态扩容思想
夏沐的博客
09-02 472
静态空间管理： 优化1：动态空间管理思路： 优化2：在原数组上固定大小扩容： 优化3：容量加倍扩容：
定义一个包含5个int类型元素长度的数组scoresArr，存储从键盘接收的5个int类型的成绩数据。 使用静态数组扩容，创建一个长度是scoresArr数组长度的2倍，将扩容多出的5个元素，用5个随机成绩数据填充。 使用冒泡法对10个成绩进行排序并输入排序后的结果。
04-23
2. 使用静态数组扩容，创建一个长度是scoresArr数组长度的2倍，将扩容多出的5个元素，用5个随机成绩数据填充： ``` int[] scoresArrDouble = Arrays.copyOf(scoresArr, scoresArr.length*2); Random random = new ...
定义一个包含5个int类型元素长度的数组scoresArr，存储从键盘接收的5个int类型的成绩数据。 //使用静态数组扩容，创建一个长度是scoresArr数组长度的2倍，将扩容多出的5个元素，用5个随机成绩数据填充。 //使用冒泡法对10个成绩进行排序并输入排序后的结果。
04-23
如果你想使用静态数组扩容，可以这样创建一个长度是scoresArr数组长度的2倍的数组newScoresArr，并将扩容多出的5个元素用5个随机成绩数据填充： ```java int[] newScoresArr = new int[scoresArr.length * 2]; ...
数据结构--冒泡排序和快速排序
qq_35297945的博客
02-25 465
1 交换排序 根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置，交换排序的特点是：将键值较大的记录向序列的尾部移动，键值较小的记录向序列的前部移动。 2 冒泡排序 2.1 基本思想 在区间[0,n-1]中，相邻元素进行比较，大的元素向后移动，并减小区间，在[0,n-2]中重复上述操作，直至不再有元素的移动或者区间大小为1时排序完成。 2.2 算法示意图 2.3 程序代码 #include<stdio.h> #include<stdlib.h> void swap(i
数组扩容、头插尾插
最新发布
likeyi_lky的博客
08-11 346
数组扩容，二分查找法，链表头插尾插
0520-ArrayList扩容算法
Domingo_Leung的博客
05-20 348
ArrayList扩容算法 private void grow(int minCapacity) { // overflow-conscious code int oldCapacity = elementData.length; int newCapacity = oldCapacity + (oldCapacity >> 1); if (newCap...
数组的动态扩容、选择排序、冒泡排序、插入排序、计数排序的解析
qq_45767166的博客
02-17 138
1.数组的动态扩容 1.1 图解 1.2 代码解释 import java.util.*; class D1{ public static void main(String[] args){ Scanner scanner=new Scanner(System.in); //数组的动态扩容 //建立一个数组长度为零的数组 ...
数组扩容的那点事
weixin_41038852的博客
12-17 1008
1、最近对数组扩容有点感兴趣，发现技术真是个好东西，当你深入了解的时候，你会发现许多有趣的事。比如数组的功能就是，在实际项目开发中，我们使用数组的频率是非常高的。因此，正确使用数组，会使用数组功能是非常有必要的。来让我们了解一下数组的功能特征： Java数组扩容的原理 　　1）、Java数组对象的大小是固定不变的，数组对象是不可扩容的。 　　2）、System.arraycopy()能够对数...
09-java学习-数组-冒泡排序-选择排序-数组工具类编写-查找-扩容
weixin_30341745的博客
03-06 132
数组的排序算法 查找算法 数组协助类Arrays的学习和使用 数组的扩容 转载于:https://www.cnblogs.com/Tpf386/p/10485874.html
数组扩容--无序数组
AI梦想家
01-05 271
数据结构 数组扩容–如何对一个数组进行有效的扩容 静态空间管理：开辟内部数组并适用一段地址连续的物理空间，capacity为总容量，size为当前的实际规模。若采用静态空间策略管理，容量capacity固定，则存在明显的不足。 上溢：capacity空间不够，不足以存放所有元素 下溢：capcity空间过大，存放的元素寥寥无几，装填因子（load factor） u=size/capacity ...
数组 ，数组内存和扩容
qq_50856002的博客
07-16 686
(1) 先声明，再分配空间：数据类型[] 数组名;数组名 = new 数据类型[长度];int[] a;(2) 声明的同时，分配空间：数据类型[] 数组名 = new 数据类型[长度];(3) 声明的同时初始化：数据类型[] 数组名 = new 数据类型[]{数据1,数据2,数组3};注意：{}中的个数决定了数组长度。数组的长度不在[]中指定(4) 声明的同时并初始化：数据类型[] 数组名 = {数据1,数据2,数据3};注意：初始化必须和声明一起完成int[] a;
数组扩容（俩种方法）
qq_23306089的博客
07-03 3764
数组扩容—扩大/小数组容器的容量（长度）—数组复制实现----数组定义完成之后长度无法改变。 数组的复制(原数组,拷贝的起始下标,目标数组,粘贴的起始下标,复制的元素个数) System.arraycopy(arr1,0,arr2,0,arr1.length); (原数组,新长度) arr1=Arrays.copyOf(arr1,arr1.length-1); /* 数组扩容 */ import java.util.Arrays; class ArrayKuoDemo{ public static void
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值