信号完整性分析7——传输线的物理基础

信号完整性分析7——传输线的物理基础

• 传输线定义： 同轴电缆线是一种传输线，多层板中的PCB线条也是一种传输线。

简单地说，传输线是由两条有一定长度的导线组成的。

• 作用： ：在可接受的失真度下， 把信号从一端传输到另—端

• 两个非常重要的特征： 特性阻抗和时延。

信号与传输线的相互作用关系比较特别，与其他三种理想电路元件（电阻、电容和电感）和信号的相互作用截然
不同。

7.1 不再使用“地”这个字

通常，我们将传输线的返回路径当做地线。将第二条线当做地，所引出的问题要比解决的问题多得多。相反，使用返回路径是一个良好的
习惯。

当把另一条路径当做地时，通常将它看成是所有电流的汇合点。返回电流从这一点流入，然后流到另一处有地节点的地方。这是一种完全错误的观点。返回电流是紧靠着信号电流的。前面讲到，高频时．信号路径和返问路径的回路电感要最小化，这就意味着只要导体的情况
允许，返回路径会尽量靠近信号路径分布。再者，由返回电流并不能得到返回路径的绝对电压。实际中．返回路径有时是个电压平面，
如VCC或VDD平面，而有时是一个低电压平面。

7.2 信号

当两条线一样时，如双绞线。信号路径与返回路径没有严格的区分，即可以指定任意一条为信号路径，而另一条为返回路径，如果两条导线不相同，如微带线，则通常把较窄的那条叫做信号路径．而把平面称为返回路径。

信号总是指信号路径和返回路径之间相邻两点的电压。

如果知道信号受到的阻抗，根据信号大小就可以计算出电流。从这个意义上讲，信号可以被定义成电压或电流。

这些普遍的原则适用于所有传输线．无论是单端传输线还是差分传输线。

7.3 均匀传输线

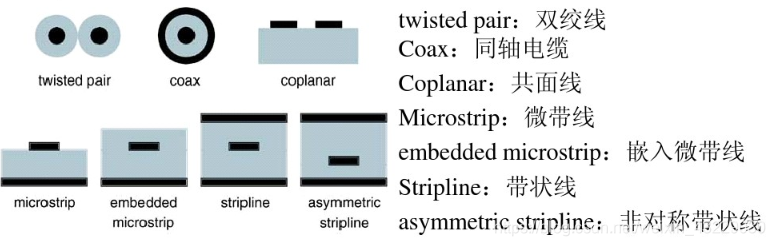
几何结构中有两个基本特征完全决定了传输线的电气特性：它们是 导线沿线横截面的均匀程度 和两导线的相似程度 。

---

导线沿线横截面的均匀程度

• 如何定义均匀？： 如果导线上任何一处的横截面都相同，比如同轴电缆，则称这种传输线为均匀传输线

• 均匀传输线也称为可控阻抗传输线。传输线的种类很多，如双引线、微带线、带状线和共面线等。

• 如果传输线是均匀的或者是有可控阻抗的，那么反射就会减小， 信号的质量就会更优。所有的高速互连线都必须设计成均匀传输线。

• 如何定义不均匀？： 整条导线中。若几何结构或材料属性发生变化传输线就是不均匀的。例如，如果两条导线的间距是变化的而不是恒定的， 那么它就是非均匀传输线。非均匀传输线除非走线足够短，否则就会引起信号完整性问题，所以应避免这种情况发生。

在信号完整性的优化设计过程中，其中一个设计目标就是：将所有的互连线都设计成均匀传输线，减小所有非均匀传输线的长度

两导线的相似程度

• 如何定义平衡（是否相似）？： 如果两导线的形状和大小都一样， 即它们是对称的，就称这种传输线为平衡传输线。e.g. 双绞线，共面线

• **非平衡传输线：**同轴电缆（中心导线要比外面的导线小），微带线（两条导线宽度不一样），带状线

一般来说， 绝大多数传输线，无论是平衡的还是非平衡的。它们对信号的质量和串扰效应都完全没有影响， 然而，返回路径的具体结构将严重影响地弹和电磁干扰问题。

7.4 铜中的电子速度

实际常见的铜导线中的电子速度比信号的速度要低100 亿倍。

简单分析略

与空气中的光速相比．导线电子的运动速度简直就是微不足道的所以导线中电子的速度与信号的速度没有任何关系。同样，由分析可知，导线的电阻对传输线上信号的传播速度几乎没有任何影响，只有在一些极端的情况下，互连线的电阻才会影响信号的传播速度。并且这个影响是非常微小的。低电阻并不意味着信号的速度快，必须纠正这个错误的观念

7.5 传输线上的信号速度

什么决定了信号的传播速度？

1. 导体周围的材料
2. 信号在传输线导体周围空间形成的交变电磁场的建立速度
3. 信号在传输线导体周围空间形成的交变电磁场的传播速度

最简单的一种描述信号在传输线上传播的方法

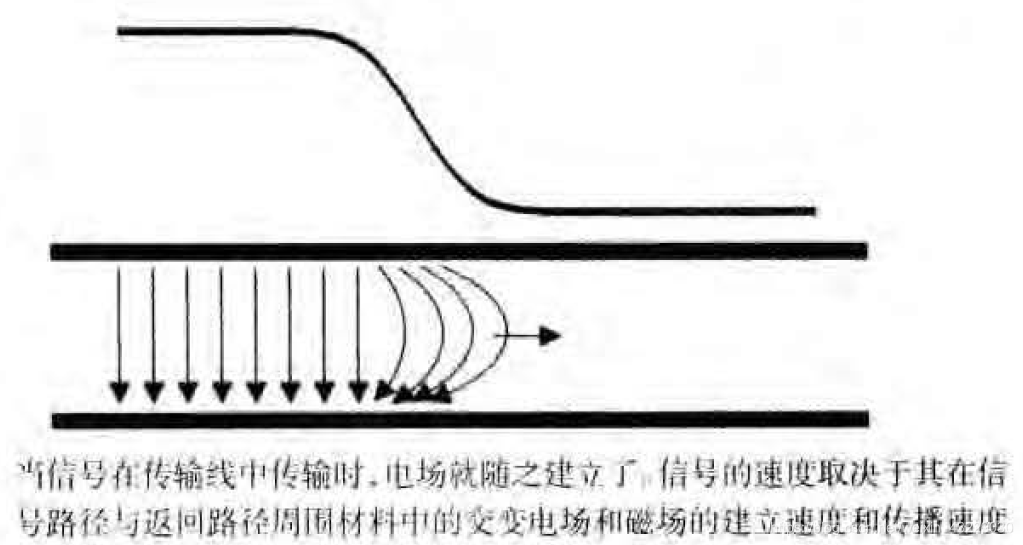
信号就是信号路径与返回路径之间的电压差。当信号线在传输线上传播时，两导线之间就会产生电压，而这个电压又使两导线之间产生电场。除了电压之外，电流必须在信号路径和返回路径上流动，这样使两导线带上了电荷并产生电压差，继而又建立的电场，而两导体之间的电流回路产生了磁场。

实际上，电场和磁场建立的快慢决定了信号的速度这些场场的传播和相互作用可以由麦克斯韦方程来描述。这就是说，只耍电场和磁场在变化，由此而形成的铰链电磁场就向外传播，它的速度取决于一些常量和材料特性。

电磁场的变化速度， 或场链的速度v由下式得到：
$$v=\frac{1}{\sqrt[]{{\epsilon }_0{\epsilon }_r{\mu }_0{\mu }_r}}$$
其中：

${\epsilon }_0$ 表示自由空间的介电常数．其值为8.89×10^-12 F/m

${\epsilon }_r$ 表示材料的相对介电常数

${\mu }_0$ 表示自由空间的导磁率，其值为4π × 10^-7 H/m

${\mu }_r$ 表示材料的相对导磁率（实际上，几乎所有的互连材料的相对导磁率都为1 。所有不含铁磁体材料的聚合物，其导
磁率都为1 。因此，导磁率这一项可以忽略。）

经验法则： 空气中，相对介电常数和相对导磁率都为1, 光的速度为12 in/ns

代入数据，可得：
$$v=\frac{12}{\sqrt[]{{\epsilon }_r{\mu }_r}}\frac{in}{ns}$$
相比之下，除了空气，其他材料的介电常数总是大于1 。所有实际互连材料的介电常数通常都大于1 。这说明互连中的光速总是小于12in/ns，其速度为：
$$v=\frac{12}{\sqrt[]{{\epsilon }_r}}\frac{in}{ns}$$
为了方便，通常将相对介电常数简称为＂介电常数”。介电常数是一个非常重要的参数，它描述了绝缘体的一些电气特征。绝大多数聚合物的介电常数约为4, 玻璃约为6, 陶瓷约为10。

材料中的光速可能与频率有关： 一般来说，随着频率的升高，介电常数会减小，这使得随着频率的升高，材料中的光速会提高。一般来说，随着频率的升高，介电常数会减小，这使得随着频率的升高，材料中的光速会提高。

经验法则： 绝大多数互连线中的光速约为12 in/ns/sqrt(4)=6 in/ns。当估算电路板上互连线中信号的连度对，就可以假定它约为6 in/ns。

时延TD 与互连线长度的关系如下：
$$TD=\frac{Len}{v}$$
其中：

$TD$ 表示时延，单位为ns

$Len$ 表示互连线长度，单位为m

$v$ 表示信号的速度，单位为in/ns

这说明当信号在 FR4 上长为 6 in 的互连线中传输时，时延约为6 叫6in/ns, 即约为1ns 。如果传输长度为12 in, 则时延为2ns 。

连线时延： 即每英寸长度互连线时延的 ps 数．也是一个非常有用的度量单位。它就是速度的倒数： 1/v

对于FR4，其连线时延约为1/6 in/ns = 0.166 ns/in, 或者170 ps/in。 所以0.5 in长的 BGA 引线的连线时延为170 ps/in x 0.5 in = 85 ps

7.6 前沿的空间延伸

信号有上升时间RT，当信号在传输线上传输时．前沿就在传输线上拓展开来，呈现出在空间上的延伸如果我们停滞时间并观察传输线上电压分布的情况．就会发现与下图所示的很相像：

传输线在上升时间内的长度d , 取决于信号的传播速度和上升时间：
$$d=RT\times v$$
其中：

$d$ 表示上升时间的空间延伸， 单位为in

$RT$ 表示信号的上升时间，单位为ns

$v$ 表示信号的速度，单位为in/ns

7.7 信号必须名副其实

当在导线上行走时，就把电压带到了两条导线体上， 并使之带电。在每纳秒时间内，都使信号前面一英尺的导线带上了电荷。信号每前进一步，就会留下另一英尺长的带电导线上。

如果信号在传输线上匀速传播．而且传输线是均匀的，即每英尺的电容直女是相等的，则每，一步注入到导线的电量也是相等的。每走一步，使等量的电容带上相等的电量，以使电容达到相同的电压。如果每走一步用的时间相同，那么单位时间要求从信号源得到的电量就相等，每纳秒流入导线的电且都相等，说明从脚上流入导线的电流是一常量。

从脚底流出的电流与单位长度的电容和信号的速度直接成比例。如果有任何一个增加，则每步从脚底流出的电流就会增加。相反，如果有任何一个减小，则来自信号使导线带电的电流就会减小。所以，从脚底流出的电流与导线特性的简单关系式为：
$$I\approx v\times C_L$$
其中：

$I$ 表示从脚底流出的电流

$v$ 表示我们在导线上行走的速度

$C_L$ 表示线的单位长度电容

当我们（信号）在传输线上行走时，就会不断地问：“导线的阻抗到底是多少?" 阻抗的基本定义是元件两端的电压与流过电流的比值。因此，当在导线上行走时，每走一步，就会不断地问，施加的电压与流过的电流之比是多少？

只要信号的速度和单位长度的电容恒定，从脚底流出的注人到导线的电流就恒延，那么信号受到的阻抗也就恒定。假设两导线的宽度突然增加，则每步间的电容就会增加，那么每步从脚底流出给电容允电的电流也会增加。电流增加而电压不变，这意味着传输线的阻抗减小。

把信号每步受到的阻抗称为传输线的瞬态阻抗。沿着传输线往下走，信号将不断地探测到每一步的瞬态阻抗。瞬态阻抗的值等于线上所加的电压与电流之比，这个电流用于传输线的充电和信号向下一步的传播。把信号每步受到的阻抗称为传输线的瞬态阻抗。沿着传输线往下走，信号将不断地探测到每一步的瞬态阻抗。瞬态阻抗的值等于线上所加的电压与电流之比，这个电流用于传输线的充电和信号向下一步的传播。

当信号遇到的瞬态阻抗变化时，一部分信号被反射，一部分更加失真，信号完整性会受到破坏。这就是对信号受到的瞬态阻抗需要加以控制的主要原因。

7.8 传输线的瞬态阻抗

可以建立一个传输线的简单物理模型来定瞿分析这个问题。线模型由一排小电容器组成，其值等于传输线一跨度的电容量，一跨度就是我们（信号）每步的间隔。把这个模型（用于工程理解的最简单的模型）称为传输线的零阶模型

在这个模型中，步长为$\Delta x$，每个小电容的大小就是传输线单位长度的电容量$C_L$与步长的乘积：
$$C=C_L\times \Delta x$$
使用这个模型，可以计算从脚底流出的电流 $I$。电流的大小就是在每步时间间隔内从脚底流出注入到每个电容上的电量。注入电容的电量$Q$，等于电容乘以其两端的电压v，每走一步，就把电量 $Q$ 注入到导线上。每步之间的时间间隔 $\Delta t$ 等于步长丛除以信号的速度 $v$ 。当然，传输实际信号时，步长非常小，但是时间间隔也非常小。每个时间间隔内需要的电量，也就是信号在导线上传播时的电流，是一个常量：
I = Q Δ t = C V ( Δ x v ) = C L Δ x v V Δ x = C L v V I= {\frac {Q}{\Delta t}}={\frac {CV}{({\frac {\Delta x}{v}})}}={\frac {C_L\Delta x v V}{\Delta x}}=C_LvV I=ΔtQ​=(vΔx​)CV​=ΔxC<