系列博客,原文在笔者所维护的github上:https://aka.ms/beginnerAI,
点击star加星不要吝啬,星越多笔者越努力。
第3章 损失函数
3.0 损失函数概论
3.0.1 概念
在各种材料中经常看到的中英文词汇有:误差,偏差,Error,Cost,Loss,损失,代价…意思都差不多,在本书中,使用“损失函数”和“Loss Function”这两个词汇,具体的损失函数符号用J来表示,误差值用loss表示。
“损失”就是所有样本的“误差”的总和,亦即(m为样本数):
损失=∑i=1m误差i损失 = \sum^m_{i=1}误差_i损失=i=1∑m误差i
J=∑i=1mlossJ = \sum_{i=1}^m lossJ=i=1∑mloss
在黑盒子的例子中,我们如果说“某个样本的损失”是不对的,只能说“某个样本的误差”,因为样本是一个一个计算的。如果我们把神经网络的参数调整到完全满足独立样本的输出误差为0,通常会令其它样本的误差变得更大,这样作为误差之和的损失函数值,就会变得更大。所以,我们通常会在根据某个样本的误差调整权重后,计算一下整体样本的损失函数值,来判定网络是不是已经训练到了可接受的状态。
损失函数的作用
损失函数的作用,就是计算神经网络每次迭代的前向计算结果与真实值的差距,从而指导下一步的训练向正确的方向进行。
如何使用损失函数呢?具体步骤:
- 用随机值初始化前向计算公式的参数;
- 代入样本,计算输出的预测值;
- 用损失函数计算预测值和标签值(真实值)的误差;
- 根据损失函数的导数,沿梯度最小方向将误差回传,修正前向计算公式中的各个权重值;
- goto 2, 直到损失函数值达到一个满意的值就停止迭代。
3.0.2 机器学习常用损失函数
符号规则:a是预测值,y是样本标签值,J是损失函数值。
-
Gold Standard Loss,又称0-1误差
loss={0a=y1a≠y loss=\begin{cases} 0 & a=y \\ 1 & a \ne y \end{cases} loss={01a=ya=y -
绝对值损失函数
loss=∣y−a∣ loss = |y-a| loss=∣y−a∣
- Hinge Loss,铰链/折页损失函数或最大边界损失函数,主要用于SVM(支持向量机)中
loss=max(0,1−y⋅a),y=±1 loss=max(0,1-y \cdot a), y=\pm 1 loss=max(0,1−y⋅a),y=±1
- Log Loss,对数损失函数,又叫交叉熵损失函数(cross entropy error)
loss=−1m∑imyilog(ai)+(1−yi)log(1−ai)yi∈{0,1} loss = -\frac{1}{m} \sum_i^m y_i log(a_i) + (1-y_i)log(1-a_i) \qquad y_i \in \{0,1\} loss=−m1i∑myilog(ai)+(1−yi)log(1−ai)yi∈{0,1}
-
Squared Loss,均方差损失函数
loss=12m∑im(ai−yi)2 loss=\frac{1}{2m} \sum_i^m (a_i-y_i)^2 loss=2m1i∑m(ai−yi)2 -
Exponential Loss,指数损失函数
loss=1m∑ime−(yi⋅ai) loss = \frac{1}{m}\sum_i^m e^{-(y_i \cdot a_i)} loss=m1i∑me−(yi⋅ai)
3.0.3 损失函数图像理解
用二维函数图像理解单变量对损失函数的影响

图3-1 单变量的损失函数图
图3-1中,纵坐标是损失函数值,横坐标是变量。不断地改变变量的值,会造成损失函数值的上升或下降。而梯度下降算法会让我们沿着损失函数值下降的方向前进。
- 假设我们的初始位置在A点,x=x0x=x0x=x0,损失函数值(纵坐标)较大,回传给网络做训练;
- 经过一次迭代后,我们移动到了B点,x=x1x=x1x=x1,损失函数值也相应减小,再次回传重新训练;
- 以此节奏不断向损失函数的最低点靠近,经历了x2、x3、x4、x5x2、x3、x4、x5x2、x3、x4、x5;
- 直到损失值达到可接受的程度,比如x5x5x5的位置,就停止训练。
用等高线图理解双变量对损失函数影响

图3-2 双变量的损失函数图
图3-2中,横坐标是一个变量www,纵坐标是另一个变量bbb。两个变量的组合形成的损失函数值,在图中对应处于等高线上的唯一的一个坐标点。w、bw、bw、b所有的不同的值的组合会形成一个损失函数值的矩阵,我们把矩阵中具有相同(相近)损失函数值的点连接起来,可以形成一个不规则椭圆,其圆心位置,是损失值为0的位置,也是我们要逼近的目标。
这个椭圆如同平面地图的等高线,来表示的一个洼地,中心位置比边缘位置要低,通过对损失函数值的计算,对损失函数的求导,会带领我们沿着等高线形成的梯子一步步下降,无限逼近中心点。
3.0.4 神经网络中常用的损失函数
-
均方差函数,主要用于回归
-
交叉熵函数,主要用于分类
二者都是非负函数,极值在底部,用梯度下降法可以求解。
系列博客,原文在笔者所维护的github上:https://aka.ms/beginnerAI,
点击star加星不要吝啬,星越多笔者越努力。
3.1 均方差函数
MSE - Mean Square Error。
该函数就是最直观的一个损失函数了,计算预测值和真实值之间的欧式距离。预测值和真实值越接近,两者的均方差就越小。
均方差函数常用于线性回归(linear regression),即函数拟合(function fitting)。公式如下:
loss=12(z−y)2(单样本) loss = {1 \over 2}(z-y)^2 \tag{单样本} loss=21(z−y)2(单样本)
J=12m∑i=1m(zi−yi)2(多样本) J=\frac{1}{2m} \sum_{i=1}^m (z_i-y_i)^2 \tag{多样本} J=2m1i=1∑m(zi−yi)2(多样本)
3.1.1 工作原理
要想得到预测值a与真实值y的差距,最朴素的想法就是用Error=ai−yiError=a_i-y_iError=ai−yi。
对于单个样本来说,这样做没问题,但是多个样本累计时,ai−yia_i-y_iai−yi有可能有正有负,误差求和时就会导致相互抵消,从而失去价值。所以有了绝对值差的想法,即Error=∣ai−yi∣Error=|a_i-y_i|Error=∣ai−yi∣。这看上去很简单,并且也很理想,那为什么还要引入均方差损失函数呢?两种损失函数的比较如表3-1所示。
表3-1 绝对值损失函数与均方差损失函数的比较
| 样本标签值 | 样本预测值 | 绝对值损失函数 | 均方差损失函数 |
|---|---|---|---|
| [1,1,1][1,1,1][1,1,1] | [1,2,3][1,2,3][1,2,3] | (1−1)+(2−1)+(3−1)=3(1-1)+(2-1)+(3-1)=3(1−1)+(2−1)+(3−1)=3 | (1−1)2+(2−1)2+(3−1)2=5(1-1)^2+(2-1)^2+(3-1)^2=5(1−1)2+(2−1)2+(3−1)2=5 |
| [1,1,1][1,1,1][1,1,1] | [1,3,3][1,3,3][1,3,3] | (1−1)+(3−1)+(3−1)=4(1-1)+(3-1)+(3-1)=4(1−1)+(3−1)+(3−1)=4 | (1−1)2+(3−1)2+(3−1)2=8(1-1)^2+(3-1)^2+(3-1)^2=8(1−1)2+(3−1)2+(3−1)2=8 |
| 4/3=1.334/3=1.334/3=1.33 | 8/5=1.68/5=1.68/5=1.6 |
可以看到5比3已经大了很多,8比4大了一倍,而8比5也放大了某个样本的局部损失对全局带来的影响,用术语说,就是“对某些偏离大的样本比较敏感”,从而引起监督训练过程的足够重视,以便回传误差。
3.1.2 实际案例
假设有一组数据如图3-3,我们想找到一条拟合的直线。
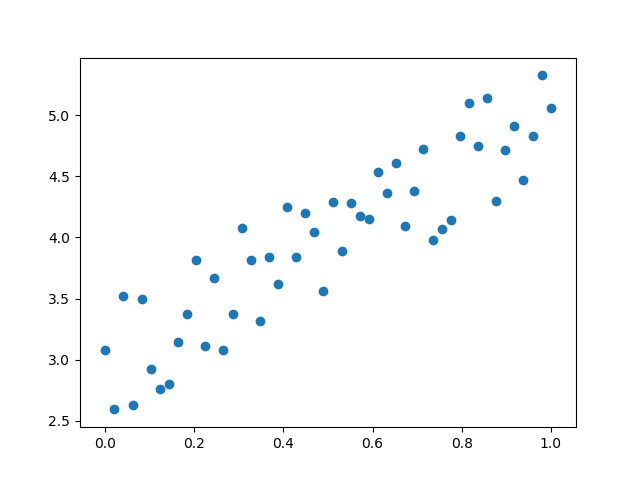
图3-3 平面上的样本数据
图3-4中,前三张显示了一个逐渐找到最佳拟合直线的过程。
- 第一张,用均方差函数计算得到Loss=0.53;
- 第二张,直线向上平移一些,误差计算Loss=0.16,比图一的误差小很多;
- 第三张,又向上平移了一些,误差计算Loss=0.048,此后还可以继续尝试平移(改变b值)或者变换角度(改变w值),得到更小的损失函数值;
- 第四张,偏离了最佳位置,误差值Loss=0.18,这种情况,算法会让尝试方向反向向下。
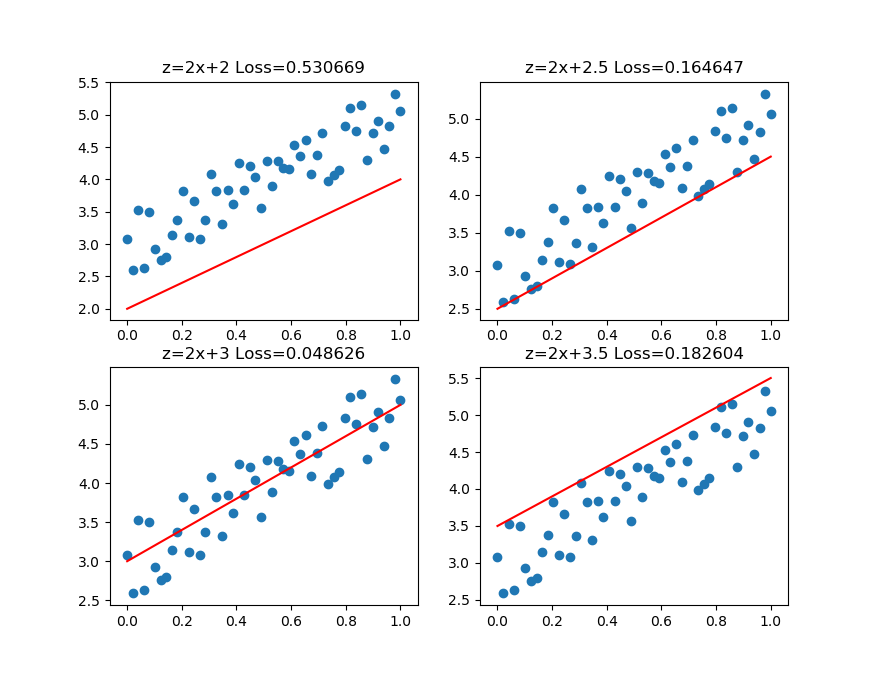
图3-4 损失函数值与直线位置的关系
第三张图损失函数值最小的情况。比较第二张和第四张图,由于均方差的损失函数值都是正值,如何判断是向上移动还是向下移动呢?
在实际的训练过程中,是没有必要计算损失函数值的,因为损失函数值会体现在反向传播的过程中。我们来看看均方差函数的导数:
∂J∂ai=ai−yi \frac{\partial{J}}{\partial{a_i}} = a_i-y_i ∂ai∂J=ai−yi
虽然(ai−yi)2(a_i-y_i)^2(ai−yi)2永远是正数,但是ai−yia_i-y_iai−yi却可以是正数(直线在点下方时)或者负数(直线在点上方时),这个正数或者负数被反向传播回到前面的计算过程中,就会引导训练过程朝正确的方向尝试。
在上面的例子中,我们有两个变量,一个w,一个b,这两个值的变化都会影响最终的损失函数值的。
我们假设该拟合直线的方程是y=2x+3,当我们固定w=2,把b值从2到4变化时,看看损失函数值的变化如图3-5所示。
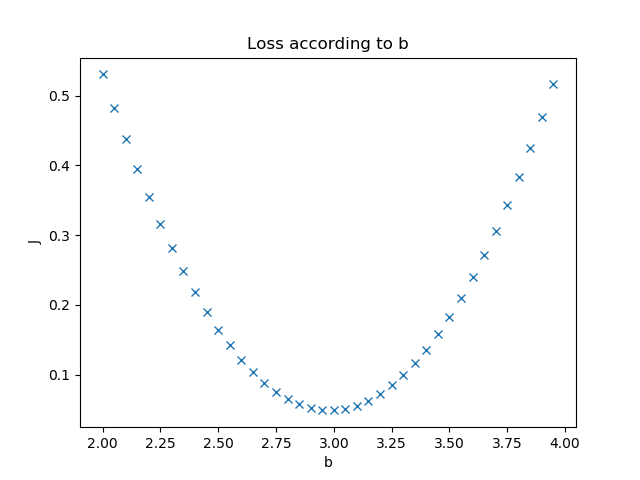
图3-5 固定W时,b的变化造成的损失值
我们假设该拟合直线的方程是y=2x+3,当我们固定b=3,把w值从1到3变化时,看看损失函数值的变化如图3-6所示。
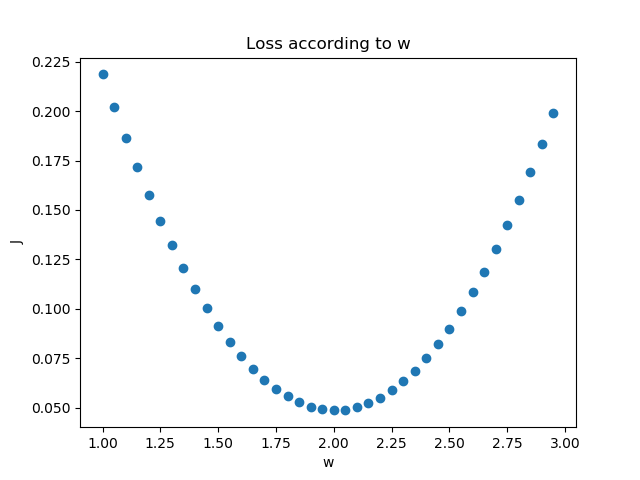
图3-6 固定b时,W的变化造成的损失值
3.1.3 损失函数的可视化
损失函数值的3D示意图
横坐标为W,纵坐标为b,针对每一个w和一个b的组合计算出一个损失函数值,用三维图的高度来表示这个损失函数值。下图中的底部并非一个平面,而是一个有些下凹的曲面,只不过曲率较小,如图3-7。
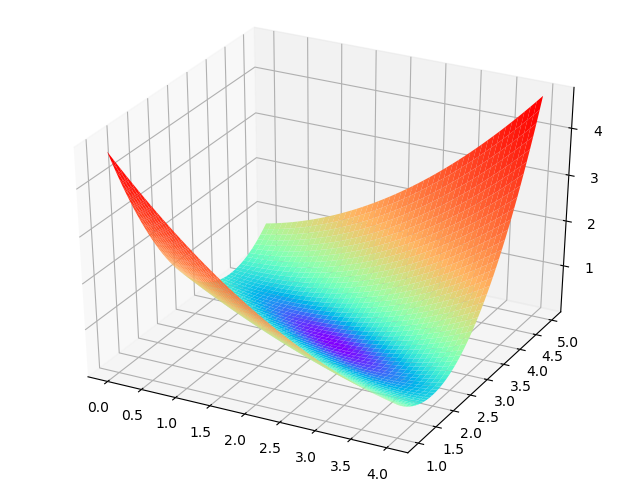
图3-7 W和b同时变化时的损失值形成的曲面
损失函数值的2D示意图
在平面地图中,我们经常会看到用等高线的方式来表示海拔高度值,下图就是上图在平面上的投影,即损失函数值的等高线图,如图3-8所示。
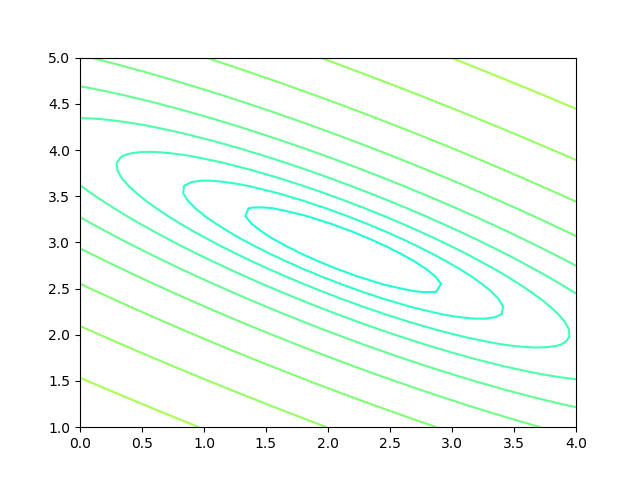
图3-8 损失函数的等高线图
如果还不能理解的话,我们用最笨的方法来画一张图,代码如下:
s = 200
W = np.linspace(w-2,w+2,s)
B = np.linspace(b-2,b+2,s)
LOSS = np.zeros((s,s))
for i in range(len(W)):
for j in range(len(B)):
z = W[i] * x + B[j]
loss = CostFunction(x,y,z,m)
LOSS[i,j] = round(loss, 2)
上述代码针对每个w和b的组合计算出了一个损失值,保留小数点后2位,放在LOSS矩阵中,如下所示:
[[4.69 4.63 4.57 ... 0.72 0.74 0.76]
[4.66 4.6 4.54 ... 0.73 0.75 0.77]
[4.62 4.56 4.5 ... 0.73 0.75 0.77]
...
[0.7 0.68 0.66 ... 4.57 4.63 4.69]
[0.69 0.67 0.65 ... 4.6 4.66 4.72]
[0.68 0.66 0.64 ... 4.63 4.69 4.75]]
然后遍历矩阵中的损失函数值,在具有相同值的位置上绘制相同颜色的点,比如,把所有值为0.72的点绘制成红色,把所有值为0.75的点绘制成蓝色…,这样就可以得到图3-9。
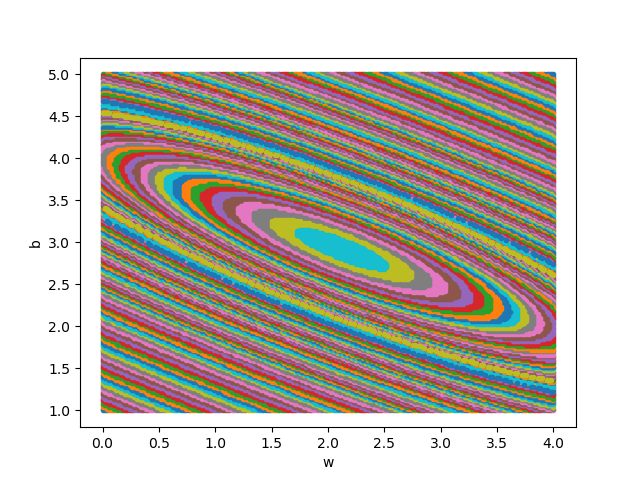
图3-9 用笨办法绘制等高线图
此图和等高线图的表达方式等价,但由于等高线图比较简明清晰,所以以后我们都使用等高线图来说明问题。
代码位置
ch03, Level1
系列博客,原文在笔者所维护的github上:https://aka.ms/beginnerAI,
点击star加星不要吝啬,星越多笔者越努力。
3.2 交叉熵损失函数
交叉熵(Cross Entropy)是Shannon信息论中一个重要概念,主要用于度量两个概率分布间的差异性信息。在信息论中,交叉熵是表示两个概率分布 p,qp,qp,q 的差异,其中 ppp 表示真实分布,qqq 表示非真实分布,那么H(p,q)H(p,q)H(p,q)就称为交叉熵:
H(p,q)=∑ipi⋅ln1qi=−∑ipilnqi(1)H(p,q)=\sum_i p_i \cdot \ln {1 \over q_i} = - \sum_i p_i \ln q_i \tag{1}H(p,q)=i∑pi⋅lnqi1=−i∑pilnqi(1)
交叉熵可在神经网络中作为损失函数,ppp 表示真实标记的分布,qqq 则为训练后的模型的预测标记分布,交叉熵损失函数可以衡量 ppp 与 qqq 的相似性。
交叉熵函数常用于逻辑回归(logistic regression),也就是分类(classification)。
3.2.1 交叉熵的由来
信息量
信息论中,信息量的表示方式:
I(xj)=−ln(p(xj))(2)I(x_j) = -\ln (p(x_j)) \tag{2}I(xj)=−ln(p(xj))(2)
xjx_jxj:表示一个事件
p(xj)p(x_j)p(xj):表示xjx_jxj发生的概率
I(xj)I(x_j)I(xj):信息量,xjx_jxj越不可能发生时,它一旦发生后的信息量就越大
假设对于学习神经网络原理课程,我们有三种可能的情况发生,如表3-2所示。
表3-2 三种事件的概论和信息量
| 事件编号 | 事件 | 概率 ppp | 信息量 III |
|---|---|---|---|
| x1x_1x1 | 优秀 | p=0.7p=0.7p=0.7 | I=−ln(0.7)=0.36I=-\ln(0.7)=0.36I=−ln(0.7)=0.36 |
| x2x_2x2 | 及格 | p=0.2p=0.2p=0.2 | I=−ln(0.2)=1.61I=-\ln(0.2)=1.61I=−ln(0.2)=1.61 |
| x3x_3x3 | 不及格 | p=0.1p=0.1p=0.1 | I=−ln(0.1)=2.30I=-\ln(0.1)=2.30I=−ln(0.1)=2.30 |
WoW,某某同学不及格!好大的信息量!相比较来说,“优秀”事件的信息量反而小了很多。
熵
H(p)=−∑jnp(xj)ln(p(xj))(3)H(p) = - \sum_j^n p(x_j) \ln (p(x_j)) \tag{3}H(p)=−j∑np(xj)ln(p(xj))(3)
则上面的问题的熵是:
H(p)=−[p(x1)lnp(x1)+p(x2)lnp(x2)+p(x3)lnp(x3)]=0.7×0.36+0.2×1.61+0.1×2.30=0.804 \begin{aligned} H(p)&=-[p(x_1) \ln p(x_1) + p(x_2) \ln p(x_2) + p(x_3) \ln p(x_3)] \\ &=0.7 \times 0.36 + 0.2 \times 1.61 + 0.1 \times 2.30 \\ &=0.804 \end{aligned} H(p)=−[p(x1)lnp(x1)+p(x2)lnp(x2)+p(x3)lnp(x3)]=0.7×0.36+0.2×1.61+0.1×2.30=0.804
相对熵(KL散度)
相对熵又称KL散度,如果我们对于同一个随机变量 xxx 有两个单独的概率分布 P(x)P(x)P(x) 和 Q(x)Q(x)Q(x),我们可以使用 KL 散度(Kullback-Leibler (KL) divergence)来衡量这两个分布的差异,这个相当于信息论范畴的均方差。
KL散度的计算公式:
DKL(p∣∣q)=∑j=1np(xj)lnp(xj)q(xj)(4)D_{KL}(p||q)=\sum_{j=1}^n p(x_j) \ln{p(x_j) \over q(x_j)} \tag{4}DKL(p∣∣q)=j=1∑np(xj)lnq(xj)p(xj)(4)
nnn 为事件的所有可能性。DDD 的值越小,表示 qqq 分布和 ppp 分布越接近。
交叉熵
把上述公式变形:
DKL(p∣∣q)=∑j=1np(xj)lnp(xj)−∑j=1np(xj)lnq(xj)=−H(p(x))+H(p,q)(5) \begin{aligned} D_{KL}(p||q)&=\sum_{j=1}^n p(x_j) \ln{p(x_j)} - \sum_{j=1}^n p(x_j) \ln q(x_j) \\ &=- H(p(x)) + H(p,q) \end{aligned} \tag{5} DKL(p∣∣q)=j=1∑np(xj)lnp(xj)−j=1∑np(xj)lnq(xj)=−H(p(x))+H(p,q)(5)
等式的前一部分恰巧就是p的熵,等式的后一部分,就是交叉熵:
H(p,q)=−∑j=1np(xj)lnq(xj)(6)H(p,q) =- \sum_{j=1}^n p(x_j) \ln q(x_j) \tag{6}H(p,q)=−j=1∑np(xj)lnq(xj)(6)
在机器学习中,我们需要评估label和predicts之间的差距,使用KL散度刚刚好,即DKL(y∣∣a)D_{KL}(y||a)DKL(y∣∣a),由于KL散度中的前一部分H(y)H(y)H(y)不变,故在优化过程中,只需要关注交叉熵就可以了。所以一般在机器学习中直接用交叉熵做损失函数来评估模型。
loss=−∑j=1nyjlnaj(7)loss =- \sum_{j=1}^n y_j \ln a_j \tag{7}loss=−j=1∑nyjlnaj(7)
其中,nnn 并不是样本个数,而是分类个数。所以,对于批量样本的交叉熵计算公式是:
J=−∑i=1m∑j=1nyijlnaij(8)J =- \sum_{i=1}^m \sum_{j=1}^n y_{ij} \ln a_{ij} \tag{8}J=−i=1∑mj=1∑nyijlnaij(8)
mmm 是样本数,nnn 是分类数。
有一类特殊问题,就是事件只有两种情况发生的可能,比如“学会了”和“没学会”,称为0/10/10/1分布或二分类。对于这类问题,由于n=2n=2n=2,所以交叉熵可以简化为:
loss=−[ylna+(1−y)ln(1−a)](9)loss =-[y \ln a + (1-y) \ln (1-a)] \tag{9}loss=−[ylna+(1−y)ln(1−a)](9)
二分类对于批量样本的交叉熵计算公式是:
J=−∑i=1m[yilnai+(1−yi)ln(1−ai)](10)J= - \sum_{i=1}^m [y_i \ln a_i + (1-y_i) \ln (1-a_i)] \tag{10}J=−i=1∑m[yilnai+(1−yi)ln(1−ai)](10)
3.2.2 二分类问题交叉熵
把公式10分解开两种情况,当y=1y=1y=1时,即标签值是1,是个正例,加号后面的项为0:
loss=−ln(a)(11)loss = -\ln(a) \tag{11}loss=−ln(a)(11)
横坐标是预测输出,纵坐标是损失函数值。y=1意味着当前样本标签值是1,当预测输出越接近1时,损失函数值越小,训练结果越准确。当预测输出越接近0时,损失函数值越大,训练结果越糟糕。
当y=0时,即标签值是0,是个反例,加号前面的项为0:
loss=−ln(1−a)(12)loss = -\ln (1-a) \tag{12}loss=−ln(1−a)(12)
此时,损失函数值如图3-10。
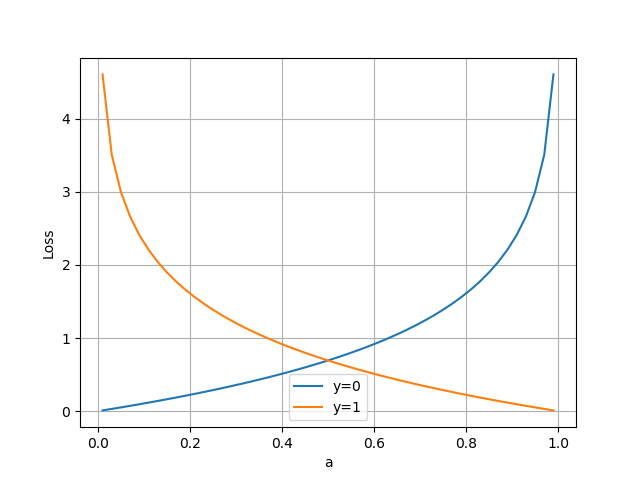
图3-10 二分类交叉熵损失函数图
假设学会了课程的标签值为1,没有学会的标签值为0。我们想建立一个预测器,对于一个特定的学员,根据出勤率、课堂表现、作业情况、学习能力等等来预测其学会课程的概率。
对于学员甲,预测其学会的概率为0.6,而实际上该学员通过了考试,真实值为1。所以,学员甲的交叉熵损失函数值是:
loss1=−(1×ln0.6+(1−1)×ln(1−0.6))=0.51 loss_1 = -(1 \times \ln 0.6 + (1-1) \times \ln (1-0.6)) = 0.51 loss1=−(1×ln0.6+(1−1)×ln(1−0.6))=0.51
对于学员乙,预测其学会的概率为0.7,而实际上该学员也通过了考试。所以,学员乙的交叉熵损失函数值是:
loss2=−(1×ln0.7+(1−1)×ln(1−0.7))=0.36 loss_2 = -(1 \times \ln 0.7 + (1-1) \times \ln (1-0.7)) = 0.36 loss2=−(1×ln0.7+(1−1)×ln(1−0.7))=0.36
由于0.7比0.6更接近1,是相对准确的值,所以 loss2loss2loss2 要比 loss1loss1loss1 小,反向传播的力度也会小。
3.2.3 多分类问题交叉熵
当标签值不是非0即1的情况时,就是多分类了。假设期末考试有三种情况:
- 优秀,标签值OneHot编码为[1,0,0][1,0,0][1,0,0]
- 及格,标签值OneHot编码为[0,1,0][0,1,0][0,1,0]
- 不及格,标签值OneHot编码为[0,0,1][0,0,1][0,0,1]
假设我们预测学员丙的成绩为优秀、及格、不及格的概率为:[0.2,0.5,0.3][0.2,0.5,0.3][0.2,0.5,0.3],而真实情况是该学员不及格,则得到的交叉熵是:
loss1=−(0×ln0.2+0×ln0.5+1×ln0.3)=1.2 loss_1 = -(0 \times \ln 0.2 + 0 \times \ln 0.5 + 1 \times \ln 0.3) = 1.2 loss1=−(0×ln0.2+0×ln0.5+1×ln0.3)=1.2
假设我们预测学员丁的成绩为优秀、及格、不及格的概率为:[0.2,0.2,0.6][0.2,0.2,0.6][0.2,0.2,0.6],而真实情况是该学员不及格,则得到的交叉熵是:
loss2=−(0×ln0.2+0×ln0.2+1×ln0.6)=0.51 loss_2 = -(0 \times \ln 0.2 + 0 \times \ln 0.2 + 1 \times \ln 0.6) = 0.51 loss2=−(0×ln0.2+0×ln0.2+1×ln0.6)=0.51
可以看到,0.51比1.2的损失值小很多,这说明预测值越接近真实标签值(0.6 vs 0.3),交叉熵损失函数值越小,反向传播的力度越小。
3.2.4 为什么不能使用均方差做为分类问题的损失函数?
-
回归问题通常用均方差损失函数,可以保证损失函数是个凸函数,即可以得到最优解。而分类问题如果用均方差的话,损失函数的表现不是凸函数,就很难得到最优解。而交叉熵函数可以保证区间内单调。
-
分类问题的最后一层网络,需要分类函数,Sigmoid或者Softmax,如果再接均方差函数的话,其求导结果复杂,运算量比较大。用交叉熵函数的话,可以得到比较简单的计算结果,一个简单的减法就可以得到反向误差。





 本文详细介绍了损失函数在神经网络中的作用和常见类型,包括均方差和交叉熵损失函数。通过图像和实际案例解释了损失函数如何指导网络训练,并探讨了为何在分类问题中不应使用均方差函数。内容涵盖了损失函数的概念、常用函数及其工作原理,并提供了代码位置以供深入学习。
本文详细介绍了损失函数在神经网络中的作用和常见类型,包括均方差和交叉熵损失函数。通过图像和实际案例解释了损失函数如何指导网络训练,并探讨了为何在分类问题中不应使用均方差函数。内容涵盖了损失函数的概念、常用函数及其工作原理,并提供了代码位置以供深入学习。
















 1929
1929

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








