有向图的两种存储类型创建和两种遍历
任务: 给定一个有向图,实现图的深度优先, 广度优先遍历算法,并输出相关结果。
功能要求: 输入图的基本信息,并建立图存储结构(有相应提示),输出遍历序列。
相关具体实验图形如下:

有向图信息:
顶点6个: A,B,C,D,E,F
8条边: A->B,A->D,A->F,B->E,C->E,D->E,F->C,C->E
深度优先遍历结果: A B C E D F
广度优先遍历结果: A B D F C E
注意事项
在命令行输入时请以英文形式输入
例如:printf("第%d条边:",k); scanf("%c,%c",&vex1,&vex2);
输入:A,B[Enter]
文章目录
(一)图的结构体、队列、标记数组的声明
1. 变量、队列等声明
#include <stdio.h>
#include <malloc.h>
#define MAXVEX 50
int visited[MAXVEX]; //为遍历准备的标志数组全局变量
char enter; //吃scnaf %c中[enter]键
//广度遍历中需使用到队列
//队列的结构体
typedef struct SqQueue{
int vex[MAXVEX];
}Queue;
//队列的全局变量
int front;
int rear;
2. 邻接链表的结构体
//邻接链表的结构体
typedef struct edge{ //边结点
int adjvex;
char vex;
struct edge *next;
}ELink;
typedef struct vex{ //顶点结点
char vex;
ELink * first;
}VLink;
typedef struct list{ //链表信息
int vexnum; //顶点数目
int arcnum; //边数目
VLink Vex[MAXVEX]; //顶点矩阵
}List;
3. 邻接矩阵的结构体
typedef struct Node{
int arcs[MAXVEX][MAXVEX]; //邻接矩阵
char vex[MAXVEX]; // 顶点值
int vexnum; //顶点数目
int arcnum; //边数目
}Adj;
4. 初始化标记数组、队列、获取顶点位置
//标志数组初始化
void initialvisitedadj(Adj G){//邻接矩阵类型的初始化
for(int i = 1;i<=G.vexnum;i++){
visited[i] = 0;
}
}
void initialvisitedlist(List list){//邻接链表类型的初始化
for(int i = 1;i<=list.vexnum;i++){
visited[i] = 0;
}
}
//队列的初始化
void initialqueue(){
front = -1;
rear = -1;
}
//获取顶点位置
int locatevex(Adj G, int v) {
int i;
for ( i = 1; i <= G.vexnum; i++) {
if (G.vex[i] == v) {
return i;
}
}
return 0;
}
(二)有向图的创建
1. 邻接矩阵存储的创建
Adj Create(Adj G){
int i,j,k;
char vex1,vex2;
printf("请输入有向图中的顶点数和边数:\n");
scanf("%d,%d",&G.vexnum,&G.arcnum);
for(i = 1;i<=G.vexnum;i++) //先把所有数组顶点设置为0;
{
for(j = 1;j<=G.vexnum;j++)
{
G.arcs[i][j] = 0;
}
}
printf("请输入有向图中%d个顶点:\n",G.vexnum);
for(i = 1;i<=G.vexnum;i++)
{
scanf("%c",&enter);
printf("输入第%d个顶点:",i);
scanf("%c",&G.vex[i]);
}
printf("请输入有向图的%d条边\n",G.arcnum);
for(k = 1;k<=G.arcnum;k++)
{
scanf("%c",&enter);
printf("第%d条边:",k);
scanf("%c,%c",&vex1,&vex2);
printf("%c<--->%c\n",vex1,vex2);
i = locatevex(G, vex1);
j = locatevex(G, vex2);
G.arcs[i][j] = 1;
}
return G;
}
2. 邻接链表的创建
//创建邻接链表
List createlist(List list){
Adj G; //创建邻接矩阵 得到G.arcs[i][j] 矩阵 根据矩阵标记0/1创建链表
int i,j,k;
char vex1,vex2;
printf("请输入有向图中的顶点数和边数:\n");
scanf("%d,%d",&G.vexnum,&G.arcnum);
for(i = 1;i<=G.vexnum;i++) //先把所有数组顶点设置为0;
{
for(j = 1;j<=G.vexnum;j++)
{
G.arcs[i][j] = 0;
}
}
printf("请输入有向图中%d个顶点:\n",G.vexnum);
for(i = 1;i<=G.vexnum;i++)
{
scanf("%c",&enter);
printf("输入第%d个顶点:",i);
scanf("%c",&G.vex[i]);
}
printf("请输入有向图的%d条边\n",G.arcnum);
for(k = 1;k<=G.arcnum;k++)
{
scanf("%c",&enter);
printf("第%d条边:",k);
scanf("%c,%c",&vex1,&vex2);
printf("%c<--->%c\n",vex1,vex2);
i = locatevex(G, vex1);
j = locatevex(G, vex2);
G.arcs[i][j] = 1;
}
//邻接链表的创建开始
for(i =1;i<=G.vexnum;i++){ //邻接链表顶点结点的初始化
list.Vex[i].vex = G.vex[i];
list.Vex[i].first = NULL;
}
ELink *p =NULL; //创建边结点
for(i=1 ;i<=G.vexnum;i++)
for(j=G.vexnum ; j>0 ;j--) //头插法插入
if(G.arcs[i][j] != 0){ //根据邻接矩阵是否有边
p =(ELink*)malloc(sizeof(ELink));
p->adjvex = j;
p->next = list.Vex[i].first;
list.Vex[i].first = p;
}
list.arcnum = G.arcnum;
list.vexnum = G.vexnum;
return list;
}
(三)有向图的输出
1. 邻接矩阵的输出
//邻接矩阵的输出
void displayadj(Adj G){
int i,j;
for(i=1 ; i<=G.vexnum ;i++){
printf("顶点%d:",i);
for(j=1 ; j<=G.vexnum ;j++){
printf("%d ",G.arcs[i][j]);
}
printf("\n");
}
}
2. 邻接链表的输出
//邻接链表的输出
void displaylist(List list){
int i;
ELink *p;
printf("图的邻接表存储\n");
for(i=1;i <= list.vexnum ;i++)
{
p=list.Vex[i].first;
printf("编号 %d 的顶点 %c : ",i-1,list.Vex[i].vex);
while(p != NULL)
{
printf("%d -> ",p->adjvex-1); //输出邻接顶点的编号
p=p->next;
}
printf("^\n");
}
}
(四)邻接矩阵的遍历
1. 邻接矩阵的深度优先遍历
顶点编号为v 的第一个邻接点
int FirstAdj(Adj G,int v){
for(int i = 1;i<=G.vexnum;i++){
if(G.arcs[v][i]==1 && visited[i]!=1){
return i;
}
}
return -1;
}
寻找它的下一个邻接点
int NextAdj(Adj G,int v,int w)
{
for(int i = w+1 ; i<=G.vexnum;i++)
{
if(G.arcs[v][i]==1 && visited[i]!=1)
{
return i;
}
}
return -1;
}
邻接矩阵的深度优先遍历
//邻接矩阵的深度优先遍历
void DFSadj(Adj G, int v)
{
int w;
printf("%c ",G.vex[v]);
visited[v] = 1;
w = FirstAdj(G, v);
while(w != -1) {
if (visited[w]==0)
{
DFSadj(G, w);
}
w = NextAdj(G, v, w);
}
}
对图深度优先遍历的主算法如下:
void MDFSadj(Adj G) //最终深度遍历结果
{
int i;
initialvisitedadj(G);
for (i=1;i<=G.vexnum;i++)
if(visited[i]==0)
DFSadj(G,i);
}
2. 邻接矩阵的广度优先遍历
void BFSadj(Adj G,int v){
printf("%c ",G.vex[v]);
visited[v]= 1;
rear++;
Queue Q;
Q.vex[rear] =v; //入队
while(front != rear)
{
front++; //出队
v = Q.vex[front];
int w = FirstAdj(G,v);
while(w!=-1){
if(visited[w]==0){
printf("%c ",G.vex[w]);
visited[w]=1;
rear++;
Q.vex[rear] = w;
}
w = NextAdj(G,v,w);
}
}
}
对图广度优先遍历的主算法如下:
void MBFSadj(Adj G){//最终广度遍历结果
int i;
initialvisitedadj(G);
initialqueue();
for (i=1;i<=G.vexnum;i++)
if(visited[i]==0)
BFSadj(G,i);
}
(五)邻接链表的遍历
1. 邻接链表的深度优先遍历
void DFSList(List list, int v){
visited[v] = 1;
printf("%c ", list.Vex[v].vex);
ELink *p = list.Vex[v].first;
while(p!=NULL){
if(visited[p->adjvex] == 0){
DFSList(list,p->adjvex);
}
p = p->next;
}
}
2. 邻接链表的广度优先遍历
//邻接链表的广度优先遍历
void BFSList(List list){
int i;
Queue Q;
initialvisitedlist(list); //初始化标记
initialqueue(); //初始化队列
for (i=1; i<= list.vexnum; i++){
if(visited[i] == 0){
visited[i] = 1;
printf("%c ", list.Vex[i].vex);
rear++; //入队
Q.vex[rear] = i;
while (front != rear){
front++;
i = Q.vex[front]; //出队
ELink *p = list.Vex[i].first;
while (p!=NULL){
if (visited[p->adjvex] == 0){
visited[p->adjvex] = 1;
printf("%c ", list.Vex[p->adjvex].vex);
rear++;
Q.vex[rear] = p->adjvex;
}
p = p->next;
}
}
}
}
}
主函数main()
int main()
{
int i ,j;
//邻接矩阵
Adj adjmatirx;
//邻接链表
List list;
int select;
int select1;
while(1)
{
printf("\t\t\t\t请你选择图的存储结构\n");
printf("\t\t\t\t\t1.邻接矩阵存储方法\n");
printf("\t\t\t\t\t2.邻接链表存储方法\n");
printf("\t\t\t\t请输入(1/2):");
scanf("%d",&select);
switch (select){
case 1:
{
adjmatirx = Create(adjmatirx);
printf("图的邻接矩阵如下:\n\n");
displayadj(adjmatirx);
printf("\n深度遍历结果:\n");
MDFSadj(adjmatirx);
printf("\n广度遍历结果:\n");
MBFSadj(adjmatirx);
printf("\n\n");
break;
}
case 2:
{
list = createlist(list);
printf("图的邻接链表如下:\n\n");
displaylist(list);
printf("\n深度遍历结果:\n");
DFSList(list,1);
printf("\n广度遍历结果:");
BFSList(list);
printf("\n\n");
break;
}
default :
printf("错误!请输入正确的数值!");
}
printf("\t\t\t\t是否退出(1)?:");//按1退出
scanf("%d",&select1);
if(select1 == 1)
return 0;
}
}
运行结果
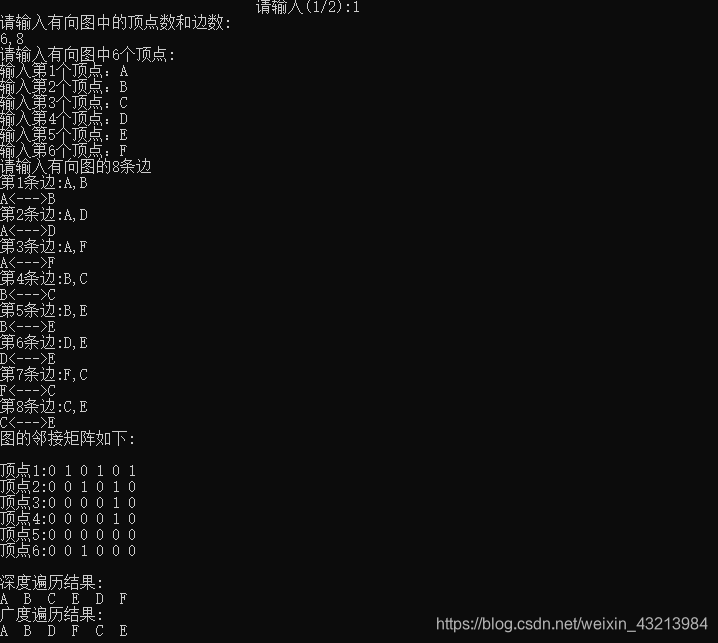
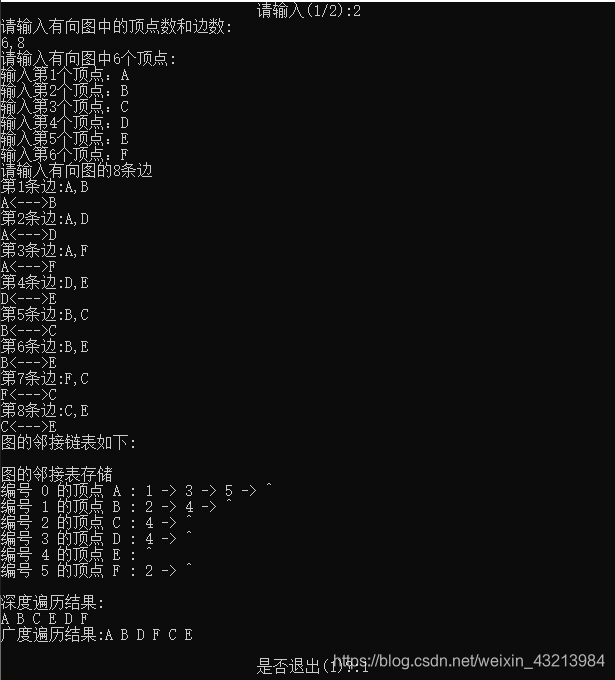




 本文介绍有向图的邻接矩阵和邻接链表两种存储方式,以及深度优先和广度优先遍历算法的实现。通过实例展示图的创建、输出及遍历过程。
本文介绍有向图的邻接矩阵和邻接链表两种存储方式,以及深度优先和广度优先遍历算法的实现。通过实例展示图的创建、输出及遍历过程。

















 5535
5535












