leetcode 69. x 的平方根&&367. 有效的完全平方数

pqlwb

于 2019-05-07 00:07:18 发布

阅读量212

点赞数

CC 4.0 BY-SA版权

分类专栏： leetcode算法题文章标签： leetcode 二分查找

本文链接：https://blog.youkuaiyun.com/weixin_43193954/article/details/89896916

leetcode算法题专栏收录该内容

4 篇文章

订阅专栏

博客先介绍二分查找需满足单调递增或递减、存在上下界、能通过索引访问三个条件，并给出Python代码模板。接着运用二分查找解决了69.X的平方根和367.有效的完全平方数两个问题，还提及X的平方根有牛顿迭代法另解。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

首先介绍下二分查找

三个条件：

sorted(单调递增或者递减)
Bounded(存在上下界)
Accessible by index(能够通过索引访问)
代码模版（python）

left, right = 0, len(array) - 1
while left <= right:
	mid = (left + right)/2
	if array[mid] == target:
		#find the target
		break(or return result)
	elif array[mid] < target:
		left = mid + 1
	else:
		right = mid -1

69.X的平方根

题目：
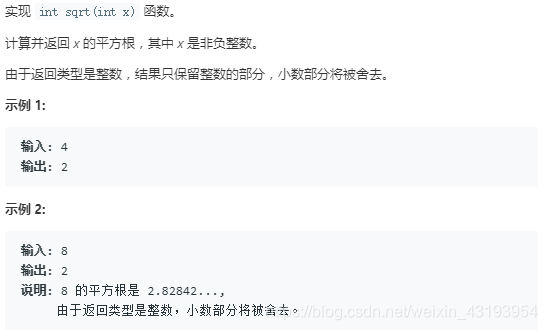
在这里插入图片描述

运用二分查找解决：

class Solution(object):
    def mySqrt(self, x):
        if x == 0 or x == 1:
            return x
        l, r = 1, x
        while l <= r:
            mid = (l+r)//2
            if mid*mid <= x < (mid+1)*(mid+1):
                return mid
            elif mid*mid > x:
                r = mid
            else:
                l = mid +1

另解：牛顿迭代法链接：牛顿迭代法

class Solution(object):
    def mySqrt(self, x):
        r = x
        while r*r > x:
            r = (r + x/r)/2
        return r

367. 有效的完全平方数

在这里插入图片描述

二分搜索解法

class Solution(object):
    def isPerfectSquare(self, num):
        if num == 1:
            return True
        l, r = 1, num
        while l <= r:
            m = l +(r-l)//2
            if m*m == num:
                return True
            elif m*m < num and (m+1)*(m+1) > num:
                return False
            elif m > num/m:
                r = m
            else:
                l = m+1

如有问题，欢迎留言