bzoj 1257:[CQOI2007] 余数之和 (分块）

（最近滚去学数论了，对我这种数学蒟蒻来说真的是痛苦）

https://www.lydsy.com/JudgeOnline/problem.php?id=1257

 

题目：给出正整数n和k，计算j(n, k)=k mod 1 + k mod 2 + k mod 3 + … + k mod n的值

其中k mod i表示k除以i的余数。

1<=n ,k<=10^9

 

（其实这题我不会做，看题解的才做出来的）

这个数据大小显然不能直接来

先将式子变形：

k mod i = k - floor(k/i) * i ,floor为下取整

那么就有：

显然n*k是可以直接求的，主要看右边那个减数。

因为那个减数有个下取整，可以看出大概 floor(k/i) 可能得到的值并不多，实际上也是如此，具体的证明是：

当i<=sqrt(k) 的时候，此时k的个数自然最多有sqrt(k)个，floor(k/i)可以得到的值也最多有sqrt(k）个

当i>=sqrt(k)的时候， floor(k/i)的值小于等于sqrt(k) , 因此floor(k/i)的值最多也只有sqrt(k)个

两者一加起来，floor(k/i)的值最多为 2*sqrt(k) 个

那么对于那个减数：

若floor(k/i)相同则分为一段，此时这个段就是等差数列，d=floor(k/i)，可以使用等差数列求和公式O(1)出结果，此时本题时间复杂度O(sqrt(k) ),可以接受

下面的问题就是如何将 floor(k/i）相同的这一段等差数列的和求出来

换个表达方式，假如我知道一段的左端点x，那么我如何求出这一段的右端点y呢？只要我能知道如何通过每一段的左端点得到右端点，我就能通过顺序计算的方法计算所有段的和

对于某个左端点x，其右端点满足：

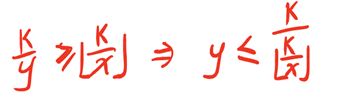
因为y是整数，所以需要来个下取整

因为y本身大于等于x,所以

然后等差数列求和就不讲了。。

#include<bits/stdc++.h>
#define ll long long 
#define ull unsigned long long
using namespace std;
const int INF = 0x3f3f3f3f;
int main() {
	ll n, k; cin >> n >> k;
	ll ans = n * k;
	for (ll i = 1, flag; i <= n; i = flag + 1) {
		flag = (k / i) ? min(k / (k / i), n) : n;
		ans -= (k / i)*(i + flag)*(flag - i + 1) / 2;
	}
	cout << ans << endl;
	return 0;
}