一、深度学习的实用层面
1.数据集
一般我们会将神经网络的数据集分成训练集(train set),验证集(dev set),测试集(test set)。一般我们要成功训练一个神经网络,难以在一开始就定下合适的超参数。我们可以先通过经验设置一个参数,再通过实验查看这个参数下训练的效果,最后对参数进行调整。如此循环,最后设定最佳的参数值。
一般来说,三个分类集的比例是6:2:2,但在数据集很大(比如大于一百万)的时候通常不需要这么大得测试集和评价集,应当将测试集和评价集的数据分给训练集,通常分1%给测试集合训练集即可。
由前文可知,评价集用于选择合适的模型,测试集用于估计模型性能,实际上有时可以不需要测试集,这时会把评价集称为测试集。
2.过拟合处理
训练神经网络模型要避免欠拟合和过拟合。判断欠拟合和过拟合通过训练集和测试集误差的来判断。解决欠拟合问题的方法使增加特征,放在神经网络模型里就是增加隐藏层神经元个数,同时增加训练数据也可以解决这个问题。
解决过拟合问题的方法有几种,比如说增加正则项。正则项有两种,分别是L1和L2正则化。
L1正则化
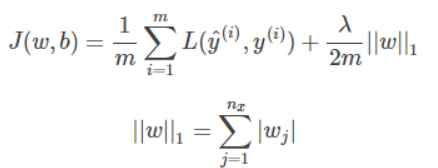
L2正则化
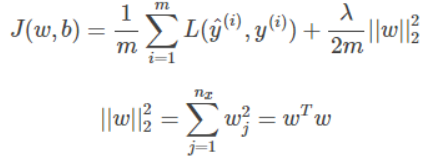
两种正则化的区别在于这个平方项,因为带平方项的正则项比较容易求导,因此实际使用中一般用L2正则项。
在神经网络模型中使用L2正则项。
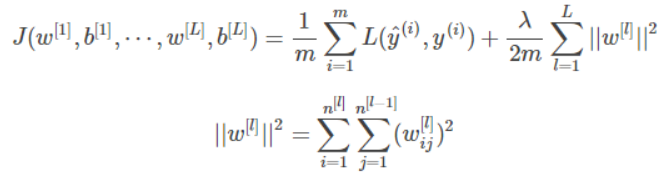
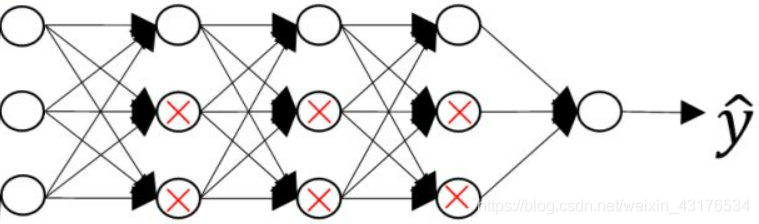
正则项对于神经网络的效果与对于普通回归模型的效果一致,主要是降低部分神经元的权重。

另一种方法是在tanh函数作为激活函数时,因为
z
[
l
]
=
w
[
l
]
a
[
l
]
+
b
[
l
]
z^{[l]}=w^{[l]}a^{[l]}+b^{[l]}
z[l]=w[l]a[l]+b[l],使用正则项可以降低参数w,则z向着中间移动到了斜率不为0的部分,整个神经网络就会发挥线性回归模型的作用,这相当于减少了特征数。
另一个防止过拟合的办法是Dropout,这个方法的原理是在每一次训练中,使每个神经元有一定概率隐藏,从而简化神经网络。具体方法有很多种,比如说Inverted dropout,这个方法在每一次训练时会依概率隐藏20%(可根据神经元的数量和实际情况进行调整)的神经元,注意为了保持隐藏这些神经元后下一层的输入值尽量不变,在隐藏这些神经元及其输入后,所得到这一层的总输入要
×
5
/
4
\times5/4
×5/4。在每次迭代都更新参数w和b,然后在下一次迭代中重新隐藏不同的神经元,直到训练结束。最后的出来的模型不隐藏任何神经元。
Dropout的作用是将输入的影响减弱了,这相当于参数的权重降低了。每一次迭代都像是一个不同的分类器,而整个分类器就相当区多个分类器的合并,这样减少了神经元之间的依赖性。
当然,还存在其他降低过拟合的方法,首先是增加训练数据,增加训练数据可以通过收集数据或是将原有数据进行各种变换获得。另外一种方法是提前停止训练。
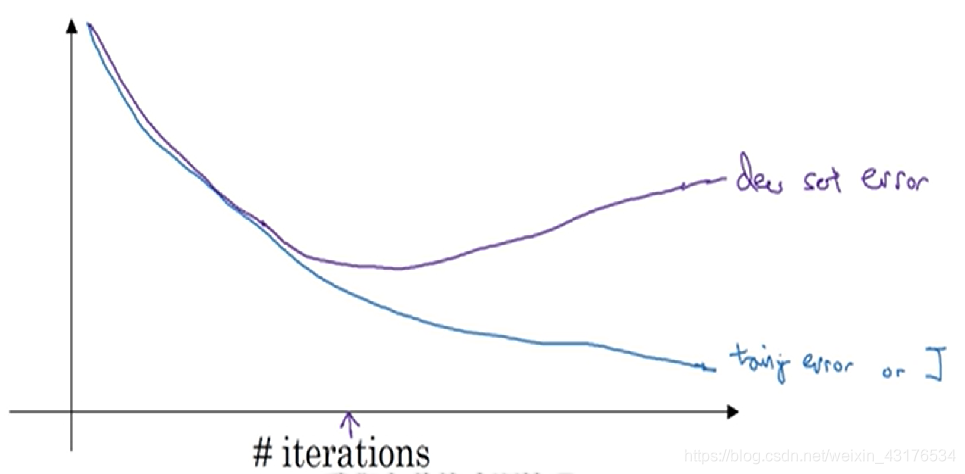
模型在训练集和测试集上的表现如上图所示,随着迭代,模型经历着由欠拟合到过拟合的过程,因此在模型处于欠拟合和过拟合之间暂停即可。当然,这个方法无法起到像正则项这样即增加准确率又避免过拟合的效果,它所得到的模型就比不上正则项训练出来的模型的准确率。它的优点是容易实现。实际上还是正则项更常用。
3.标准化输入
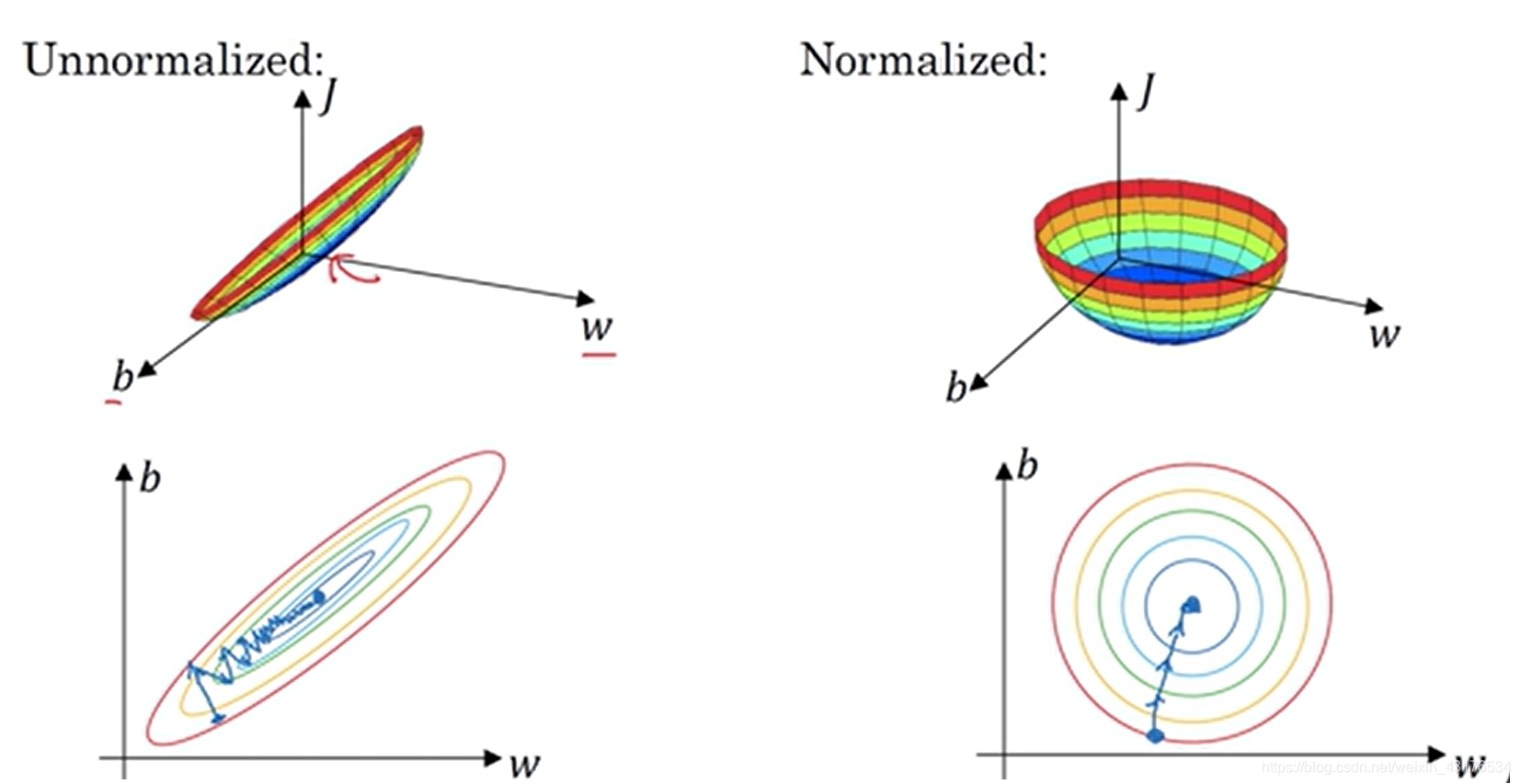
在训练模型之前应当对数据进行标准化处理,应当注意在实际使用中也要对数据进行标准化处理。标准化的好处是令代价函数平面区域圆形,这样代价函数的迭代就趋向于直线,这有利于增加训练速度。
4.梯度消失与梯度爆炸
以
g
(
z
)
=
z
g(z)=z
g(z)=z作为激活函数,那么多次迭代后神经网络的输出约为
Y
=
W
[
1
]
×
W
[
2
]
×
W
[
3
]
×
…
…
Y=W^{[1]} \times W^{[2]}\times W^{[3]}\times……
Y=W[1]×W[2]×W[3]×……,当神经元很多且系数项都大于1的话,就有可能出现梯度爆炸的问题,即输出过大的问题。同理,如果神经元系数项都小于1的话,就会出现梯度消失的问题。
改善这个问题的方法是对参数w进行初始化处理,比如让初始化的w的方差在1/n(tanh)或2/n(ReLU)。除此之外,还可以用下面的公式描述的方差:
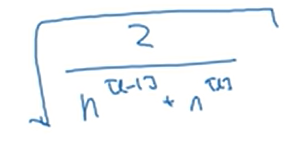
5.梯度检查
梯度检查原理与用法如上文所示,具体计算公式:
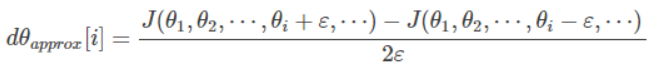








 本文详细探讨了深度学习中的关键实践,包括数据集划分、过拟合防治(L1/L2正则化、Dropout等)、标准化输入、梯度消失与爆炸的解决、以及梯度检查的原理。通过实例讲解如何有效管理和避免这些问题,提升模型性能。
本文详细探讨了深度学习中的关键实践,包括数据集划分、过拟合防治(L1/L2正则化、Dropout等)、标准化输入、梯度消失与爆炸的解决、以及梯度检查的原理。通过实例讲解如何有效管理和避免这些问题,提升模型性能。
















 799
799

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








