LeetCode 106. 从中序与后序遍历序列构造二叉树（已知后序与中序输出前序）

已知后序与中序输出前序（先序）：
后序：3, 4, 2, 6, 5, 1（左右根）
中序：3, 2, 4, 1, 6, 5（左根右）
分析：因为后序的最后一个总是根结点，令i在中序中找到该根结点，则i把中序分为两部分，左边是左子树，右边是右子树。因为是输出先序（根左右），所以先打印出当前根结点，然后打印左子树，再打印右子树。左子树在后序中的根结点为root - (end - i + 1)，即为当前根结点-右子树的个数。左子树在中序中的起始点start为start，末尾end点为i - 1.右子树的根结点为当前根结点的前一个结点root - 1，右子树的起始点start为i+1，末尾end点为end。

输出的前序应该为：1, 2, 3, 4, 5, 6（根左右）

代码：

#include <cstdio>
using namespace std;
int post[] = {3, 4, 2, 6, 5, 1};
int in[] = {3, 2, 4, 1, 6, 5};
void pre(int root, int start, int end) {
    if(start > end) return ;
    int i = start;
    while(i < end && in[i] != post[root]) i++;
    printf("%d ", post[root]);
    pre(root - 1 - end + i, start, i - 1);
    pre(root - 1, i + 1, end);
}
 
int main() {
    pre(5, 0, 5);
    return 0;
}

LeetCode 106. 从中序与后序遍历序列构造二叉树
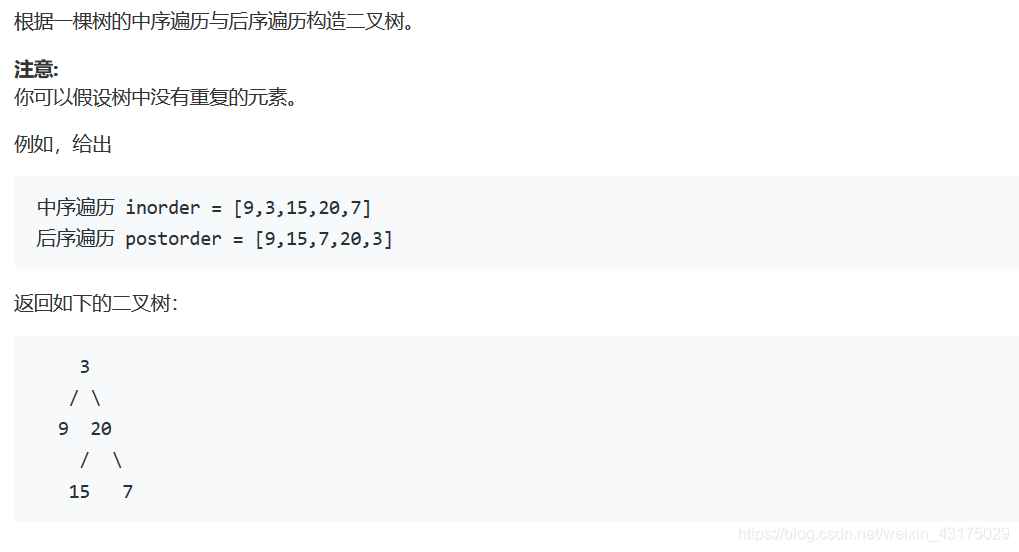代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* build(int root,int st,int end,vector<int>& inorder, vector<int>& postorder){
        if(st>end)
            return NULL;
        int i=st;
        while(i<end&&inorder[i]!=postorder[root])
            i++;
        TreeNode* t=new TreeNode(postorder[root]);
        t->left=build(root-(end-i+1),st,i-1,inorder,postorder);
        t->right=build(root-1,i+1,end,inorder,postorder);
        return t;
    }
    
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        return build(postorder.size()-1,0,postorder.size()-1,inorder,postorder);
    }
};

参考博客：https://blog.youkuaiyun.com/liuchuo/article/details/52135893