递归函数简单来说是一种自身调用自身的函数。递归函数可用于需要重复操作的程序,如绘制分形树,下面将以分形树绘制作为递归函数的实例,解释递归函数的编写方法。
递归函数的编写步骤:
1.找到并设置迭代单体
在绘制分形树的过程中,若能先完成分形树中元素的绘制,则可通过迭代操作完成整个分形树的绘制,每一步迭代所进行的操作在此定义为“迭代单体”。每次迭代操作,实际上就是一次递归调用的过程。

2.回到迭代前初始状态
实行一次迭代后,程序应回到当前层次的迭代相应的初始状态,以正确开启下一次迭代,如分形树绘制中,绘制光标应回到当前层次的起始点,如下图实心箭头的位置:
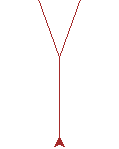
3.设置结束条件
由于递归函数所固有的自身调用自身的循环特性,因此当然需要设置结束条件才能终止程序。分形树绘制的例子中,结束条件设置为branch_length小于某一设定的值。
4.编程实现
展示一下绘制分形树的递归函数代码:
def draw_branch(branch_length):
"""
绘制分形树
"""
if branch_length > 5:
# 绘制右侧树枝
turtle.forward(branch_length)
print('向前 ', branch_length)
turtle.right(20)
print('右转 20')
draw_branch(branch_length - 15)
# 绘制左侧树枝
turtle.left(40)
print('左转 40')
draw_branch(branch_length - 15)
# 返回之前的树枝
turtle.right(20)
print('右转 20')
turtle.backward(branch_length)
print('向后 ', branch_length)
以及分形树初始条件为 branch_length = 80 的绘制结果:
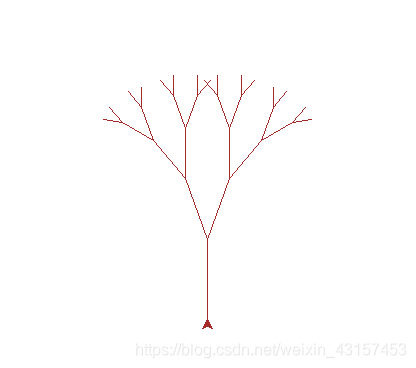








 本文以分形树绘制为例,介绍递归函数的编写方法。递归函数是自身调用自身的函数,用于重复操作。编写步骤包括找到并设置迭代单体、回到迭代前初始状态、设置结束条件,最后给出了绘制分形树的递归函数代码及初始条件为branch_length = 80的绘制结果。
本文以分形树绘制为例,介绍递归函数的编写方法。递归函数是自身调用自身的函数,用于重复操作。编写步骤包括找到并设置迭代单体、回到迭代前初始状态、设置结束条件,最后给出了绘制分形树的递归函数代码及初始条件为branch_length = 80的绘制结果。
















 1558
1558

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








