TensorFlow小程序(五)：基于卷积神经网络的MNIST识别

一、卷积神经网络简介

传统神经网络存在的问题：权值太多、计算量太大，需要大量样本进行训练。卷积神经网络（CNN）通过感受野和权值共享减少了神经网络需要训练的参数个数。
1.一个卷积神经网络主要结构组成：

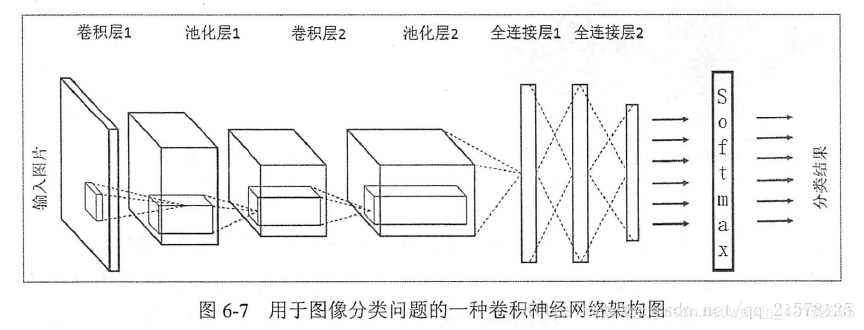
1）输入层。输入层是整个神经网络的输入，在处理图像的卷积神经网络中，它一般代表了一张图片的像素矩阵。像素矩阵一般为一个三维矩阵，它的长和宽代表了图像的大小，深度代表了图像的色彩通道。黑白图片的深度为1，RGB色彩模式下，深度为3。从输入层开始，CNN通过不同的神经网络结构将上一层的三维矩阵转化为下一层的三维矩阵，直到最后的全连接层。
2）卷积层。CNN中最重要的一个部分。和全连接层不同，卷积层中每一个节点的输入只是上一层神经网络的一小块，这个小块常用的大小为33,55。通过卷积层处理过的节点矩阵一般会变得更深。卷积层中最重要的部分为过滤器(filter)或者内核(kernel)，常用的过滤器尺寸有33或55。CNN中每一个卷积层使用的过滤器的参数都是一样的。卷积层的参数个数和图片的大小无关，它只和过滤器的尺寸、深度及当前层节点矩阵的深度有关。过滤器是横跨整个深度的。

conv=tf.nn.conv2d(input,filter_weight,strides=[1,1,1,1],padding='SAME')

第一个输入为当前层的节点矩阵
第二个参数提供了卷积层的权重
第三个参数提供的是一个长度为4的数组，第一位和最后一维的数字要求一定是1
第四个参数四填充(padding)，Tensorflow中提供SAME和VALID两种选择。
3）池化层（pooling）。池化层神经网络不会改变三维矩阵的深度，但是可以缩小矩阵的大小。通过池化层可以进一步缩小最后全连接层中节点的个数，达到减小整个神经网络中参数的目的。池化层过滤器中的计算不是节点的加权和，而是采用更加简单的最大值或者平均值运算。池化层的过滤器除了在长和宽两个维度移动之外，还需要在深度这个维度上移动。
下面是Tensorflow程序实现了最大池化层的前向传播算法：

pool=tf.nn.max_pool(actived_conv,ksize=[1,3,3,1],strides=[1,2,2,1],padding='SAME')

ksize提供了过滤器的尺寸，第一个和最后一个数必须为1，池化层使用最多分过滤器尺寸为[1,2,2,1][1,3,3,1]。
strides提供了步长信息，第一个书数和最后一个也只能为1，这意味着池化层不能减少节点矩阵的深度过输入样例的个数。
padding提供了是否使用全0填充，VALID表示不使用全0，SAME使用全0。
tf.nn.avg.pool表示平均池化层。
4）全连接层。经过几轮卷积层和池化层处理后，可以认为图像中的信息已经被抽象成了信息含量更高的特征，将卷积层和池化层看成自动图像特征提取的过程。在特征提取完成之后，仍然需要使用全连接层来完成分类任务。
5）Softmax层。Softmax层主要用于分类问题。经过Softmax层，可以得到当前样例中属于不同种类的概率分布情况。
2.利用卷积神经网络实现MNIST数字识别

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
mnist=input_data.read_data_sets('MNIST_data',one_hot=True)

#每个批次的大小
batch_size=100
#计算一共有多少个批次
n_batch=mnist.train.num_examples//batch_size

#初始化权值
def weight_variable(shape):
    initial=tf.truncated_normal(shape,stddev=0.1) #生成一个阶段的正态分布,标准差为0.1
    return tf.Variable(initial)

#初始化偏置
def bias_variable(shape):
    initial=tf.constant(0.1,shape=shape)
    return tf.Variable(initial)

#卷积层
def conv2d(x,W):            #conv2d是tensorflow中的一个二维卷积库
    return tf.nn.conv2d(x,W,strides=[1,1,1,1],padding='SAME')
    #x input tensor of shape [batch,in_height,in_width,in_channels]
    #W filter/kernel tensor of shape[filter_height,fliter_width,in_channels输入通道,out_channels输出通道]
    #strides[0]=strides[3]=1(固定为1) strides[1]代表x方向的步长,strides[2]代表y方向的步长
    #padding: A string from : 'SAME'or'VALID'

#池化层
def max_pool_2x2(x):
    return tf.nn.max_pool(x,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')
     #ksize表示窗口大小[1,x,y,1] [1,2,2,1] 表示窗口为2*2

#定义两个placeholder
x=tf.placeholder(tf.float32,[None,784]) #MNIST中28*28=784
y=tf.placeholder(tf.float32,[None,10])

#改变x的格式转化为4D的向量[batch,in_height,in_width,in_channels]
x_image=tf.reshape(x,[-1,28,28,1])  #1表示黑白照片,3为彩色照

#初始化第一个卷积层的权值和偏置
W_conv1=weight_variable([5,5,1,32]) #5*5的采样窗口,32个卷积核从1个平面抽取特征
b_conv1=bias_variable([32])  #每一个卷积核的一个偏置

#把x_image和权值向量进行卷积,再加上偏置值,然后应用于relu激活函数
h_conv1=tf.nn.relu(conv2d(x_image,W_conv1)+b_conv1)  #卷积层
h_pool1=max_pool_2x2(h_conv1)                  #池化层

#初始化第二个卷积层的权值和偏置
W_conv2=weight_variable([5,5,32,64]) #5*5的采样窗口,64个卷积核从32个平面抽取特征
b_conv2=bias_variable([64])  #每一个卷积核一个偏置值

#把h_pool1和权值向量进行卷积,再加上偏置值,然后应用于relu激活函数
h_conv2=tf.nn.relu(conv2d(h_pool1,W_conv2)+b_conv2)
h_pool2=max_pool_2x2(h_conv2)   #进行max-pooling

#28*28的图片第一次卷积后还是28*28,第一次池化后变为14*14
#第二次卷积后为14*14,第二次池化后变为7*7
#经过上面操作后得到64张7*7的平面

#初始化第一个全连接层的权值
W_fc1=weight_variable([7*7*64,1024]) #上一层有7*7*64个神经元,全连接层有1024个神经元
b_fc1=bias_variable([1024])  #1024个节点

#把池化层2的输出扁平化为1维
h_pool2_flat=tf.reshape(h_pool2,[-1,7*7*64])
#求第一个全连接层的输出
h_fc1=tf.nn.relu(tf.matmul(h_pool2_flat,W_fc1)+b_fc1)

#keep_prob用来便是神经元的输出概率
keep_prob=tf.placeholder(tf.float32)
h_fc1_drop=tf.nn.dropout(h_fc1,keep_prob)

#初始化第二个全连接层
W_fc2=weight_variable([1024,10])
b_fc2=bias_variable([10])

#计算输出
prediction=tf.nn.softmax(tf.matmul(h_fc1_drop,W_fc2)+b_fc2)

#交叉熵代价函数tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y,logits=prediction))
cross_entropy=tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y,logits=prediction))
#使用AdamOptimizer进行优化
train_step=tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
#结果存放在一个布尔列表中
correct_prediction=tf.equal(tf.argmax(prediction,1),tf.argmax(y,1)) #argmax返回一维张量中最大的值所在位置
#求准确率
accuracy=tf.reduce_mean(tf.cast(correct_prediction,tf.float32))

with tf.Session()as sess:
    sess.run(tf.global_variables_initializer())
    for epoch in range(21):
        for batch in range(n_batch):
            batch_xs,batch_ys=mnist.train.next_batch(batch_size)
            sess.run(train_step,feed_dict={x:batch_xs,y:batch_ys,keep_prob:0.7})

        acc = sess.run(accuracy, feed_dict={x: mnist.test.images, y: mnist.test.labels, keep_prob: 1.0})
        print("Iter"+str(epoch)+",Testing Accuracy="+str(acc))

运行结果：
Iter0,TestingAccuracy = 0.863
Iter1,Testing Accuracy=0.8765
Iter2,Testing Accuracy=0.9749
Iter3,Testing Accuracy=0.982
Iter4,Testing Accuracy=0.9844
Iter5,Testing Accuracy=0.9858
Iter6,Testing Accuracy=0.9871
Iter7,Testing Accuracy=0.9882
Iter8,Testing Accuracy=0.9882
Iter9,Testing Accuracy=0.9899
Iter10,Testing Accuracy=0.9896
Iter11,Testing Accuracy=0.9896
Iter12,Testing Accuracy=0.9905
Iter13,Testing Accuracy=0.9905
Iter14,Testing Accuracy=0.9904
Iter15,Testing Accuracy=0.9907
Iter16,Testing Accuracy=0.9907
Iter17,Testing Accuracy=0.9914
Iter18,Testing Accuracy=0.9919
Iter19,Testing Accuracy=0.9915
Iter20,Testing Accuracy=0.9913
与之前的准确率进行对比，利用CNN准确率达到了99%左右，很高了，说明CNN的效果非常好。

参考书：《TensorFlow实战Google深度学习框架》 郑泽宇 顾思宇 著
参考视频：https://www.bilibili.com/video/av20542427/?p=20