0_1背包问题的解法

最近自己在看一些一些算法方面的书，就看到了0_1背包问题 这应该是算法里动态规划里比较经典的算法了，相信大多数人都遇到过 ，那么怎么解决这一类问题 ，我在这儿粗略的表达一下我的看法。废话不多说先举例；

eg:现在有一些物品它们的重量w和价值p 分别为 (2,3) , (2,6) , (3,5) , (6,4) , (4,5) ,(1,3) , (5,2) , (7,7)有一背包 可以放下重量为 10 的物品物品不可拆分 问 能装下物品的最大的价值之和是多少

来分析一下这个问题最好是能画一张图这里我也画好了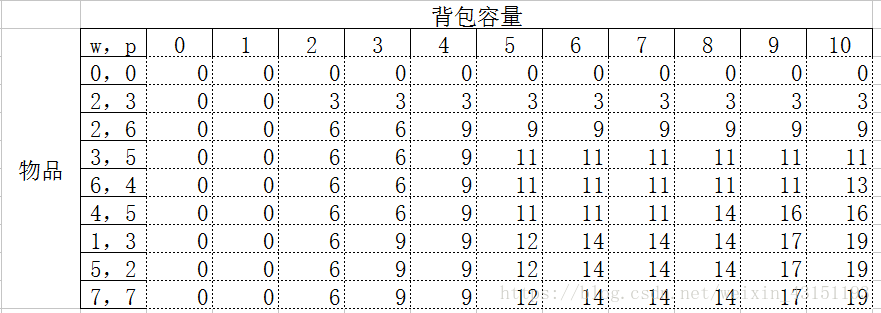

这个图是在假设背包容量递增的情况下，来记录在有一件物品 两件物品 三件物品 四件物品。。。。。。等等情况下背包所能转下的最大价值 从上往下 第一行表示没有物品可选，第二行表示 可以选择第一个物品 以此类推 而每一格的价值应该这么计算：
看当前背包容量是否能够大于这个物品的重量 然后如果大于 那么此时就看背包的容量减去这个物品的·重量加上剩余容量的最大价值p[i] + c[i - 1][j - w[i]] ，， 是否比当前不装入这个物品的价值大c[i - 1][j] ，， 如果小保持不变 c[i - 1][j] ，， 否则则为p[i] + c[i - 1][j - w[i]]
具体算法如下 ：

package javaAlgorithm;

import java.util.Scanner;
/*0_1背包问题 动态规划 这个问题里面 最重要的是c[][]充当了记忆的功能 能够记录下每一次的最大价值，那么在这样的
 * 条件下 就可以利用动态规划 每一次增加一个物品 依次比较在背包装得下这个物品时的价值是否比上次没有这个物品时的价值大
 * 通俗来讲 就是 如果此时背包的容量大于这个物品的重量 那么就比较 这个物品的价值加上背包剩余重量能装下的最大价值 是否大于
 * 上一行也就是没有这个物品时背包此时能装下的最大价值 如果是 那么此时的价值就是  这个物品的价值 加上 剩余背包能装下的最大价值
 * 如果不是 那么此时的价值就是    没有这个物品时此时背包的价值
 */
public class Zero_one_package {

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        int volume, num;//volume为背包的容量 num为物品的个数
        Scanner scanner = new Scanner(System.in);
        System.out.println("请输入背包容量和物品重量:");
        volume = scanner.nextInt();
        num = scanner.nextInt();
        System.out.println("能装下物品的最大价值是:\n" + caculate(volume, num));
        scanner.close();
    }

    private static int caculate(int volume, int num) {

        int w[] = new int[num + 1];//物品的重量
        int p[] = new int[num + 1];//物品的价值
        int c[][] = new int[num + 1][volume + 1];//存放记忆每一次计算得来的价值
        Scanner scanner = new Scanner(System.in);
        System.out.println("请输入物品重量和价值:");
        for(int i = 1; i < num + 1; i++) {
            w[i] = scanner.nextInt();
            p[i] = scanner.nextInt();
        }
        for(int i = 1; i <= num; i++) {
            for(int j = 1; j <= volume; j++) {
                if(w[i] <= j) {//如果放得下该物品
                    //那么就比较这个物品的价值加上 此时 背包的容量减去这个物品的重量(j - w[i])
                    // 得到的剩余的重量的那一列最大的价值(c[i-1][j-w[i])的和。是否大于上一行这一处的重量。 
                    if(p[i] + c[i - 1][j - w[i]] > c[i - 1][j]) {
                        //如果大于 那么现在的价值就是P[i] + c[i - 1][j - w[i]];
                        c[i][j] = p[i] + c[i - 1][j - w[i]];
                    }else {
                        //如果不大于 那么现在的价值就是c[i - 1][j]
                        c[i][j] = c[i - 1][j];
                    }
                }else {
                    //如果背包不足以装下现在物品的重量 那么价值和没有看这个物品之前一样都是处c[i -1][j];
                    c[i][j] = c[i - 1][j];
                }
            }
        }
        return c[num][volume];
    }
}