【数据结构】红黑树

概述

AVL树 是一种自平衡二叉查找树，它要求每个结点的左右子树的高度之差的绝对值（平衡因子）不超过1，所以它是一种非常严格的平衡二叉树；

红黑树（Red Black Tree） 也是一种自平衡二叉查找树，它是许多“平衡”搜索树中的一种，它可以保证在最坏情况下基本动态集合操作的时间复杂度为O(lgn)；红黑树在它的每个结点上增加了一个存储位来表示结点的颜色，可以是RED或BLACK；红黑树确保没有一条路径会比其他路径长出2倍，因而是近似于平衡的。

红黑树和AVL树都是通过旋转来达到自平衡效果的，但由于它们的平衡条件不同（AVL树更严格），所以用来维护平衡条件所付出的代价也是不同的；因此AVL树适合插入与删除次数较少，查找更多的场景；当场景中需要频繁地进行插入、删除操作时，红黑树是一种更好的选择。

性质

• 每个结点要么是黑色，要么是红色；
• 根节点是黑色；
• 每个叶子结点（NIL）是黑色；
• 每个红色结点的两个子结点一定都是黑的；
• 任意一结点到每个叶子结点的路径都包含数量相同的黑色结点。

红黑树是非完美平衡二叉查找树，是完美黑色平衡二叉查找树。

自平衡的最小单元

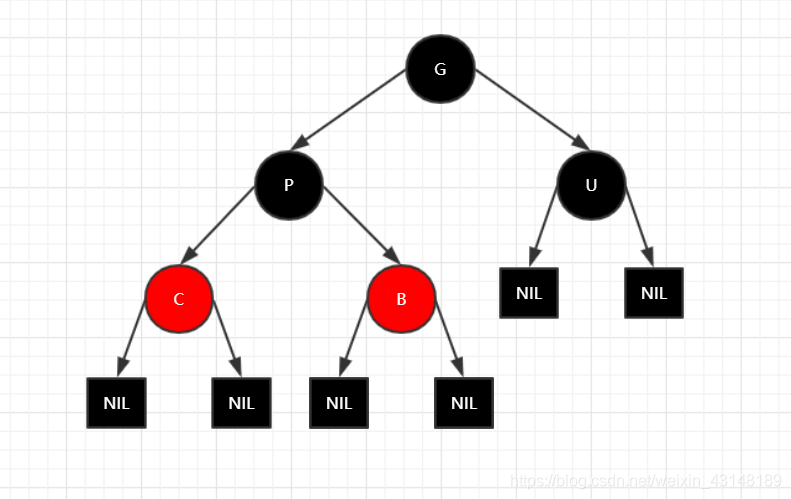
祖父母 G：Grandparents
父母 P：Parent
叔叔 U：Uncle
兄弟 B：Brother
当前新增结点 C：Current

红黑树的自平衡每次只用考虑CGPU三代即可