数据结构学习——回溯法之八皇后问题

一.八皇后问题

让八个皇后在棋盘上存在，且互相不能吃掉（即两两不能在同行、同列、同对角线上）

二.代码实现

1.主要函数

void EightQueen(int * ChessBoard)
{
	int row = 0;	
	while (row < BoardWidth)
	{
		while (ChessBoard[row] < BoardWidth)
		{
			if (NoSameCol(ChessBoard, row) && NoDiagonal(ChessBoard, row))
			{
				break;
			}

			ChessBoard[row]++;
		}

		if (ChessBoard[row] == BoardWidth)
		{
			ChessBoard[row] = 0;
			row--;
			ChessBoard[row]++;
		}
		else
		{
			row++;
		}
	}
}

2.辅助函数

1.判断是否与Row之前的行有同列的情况，无则返回 true;

bool NoSameCol(int * ChessBoard, int Row)
{
	for (int i = 0; i < Row; i++)
	{
		if (ChessBoard[i] == ChessBoard[Row])		//判断是否同行
			return false;
	}
	return true;
}

2.判断是否与Row之前有同对角线的情况，无则返回 true;

bool NoDiagonal(int * ChessBoard, int Row)
{
	//若两个点在对角线上，则这两点的行的差会等于列的差
	for (int i = 0; i < Row; i++)
	{
		if (ChessBoard[Row] > ChessBoard[i])
		{
			if (ChessBoard[Row] - ChessBoard[i] == Row - i)	
				return false;
		}
		else
		{
			if (ChessBoard[i] - ChessBoard[Row] == Row - i)
				return false;
		}
	} 
	return true;
}

3.输出效果

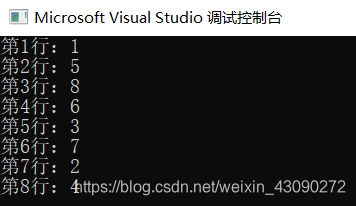
这样显然不够直观。我们把它美化一下，就得到下图：

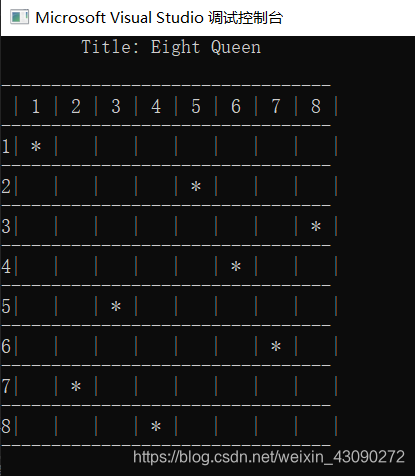
三.main函数和美化函数

1.首先是main函数

int main()
{
	EightQueen(ChessBoards);
	//1. 非直观
	//for (int i = 0; i < BoardWidth; i++)
	//{
	//	printf("第%d行：%d\n", i + 1, ChessBoards[i] + 1);
	//}
	//2.  美化从而更加直观
	printf("	Title: Eight Queen\n\n");
	OutputChess(ChessBoards);
	return 0;
}

2.接下来是美化函数

//输出棋盘
void OutputChess(int * ChessBoard)
{
	printf("---------------------------------\n");
	printf(" | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |\n");
	printf("---------------------------------");
	printf("\n");
	for (int i = 0; i < BoardWidth; i++)
	{
		printf("%d| ", i + 1);
		for (int j = 0; j < ChessBoard[i]; j++)
		{
			printf("  | ");
		}
		printf("*");
		printf(" | ");
		for (int k = ChessBoard[i] + 1; k < BoardWidth; k++)
		{
			printf("  | ");
		}
		printf("\n");
		printf("---------------------------------");
		printf("\n");
	}
}

四.手稿