Python 解方程

一·求解线性方程组Numpy
假设我们有以下方程组：形如A * x = b
$$\{\begin{array}{c}x+y=4\\ 2\ast x+3\ast y=5\end{array}$$

import numpy as np
A = np.mat('1,1; 2,3')
b = np.mat('4;5')
r = np.linalg.solve(A,b)
print (r)

二·求解非线性方程组SciPy（它同样适用于求解线性方程组。）

句法：scipy.optimize.fsolve(func, x0, args=(), fprime=None, full_output=0, col_deriv=0, xtol=1.49012e-08, maxfev=0, band=None, epsfcn=None, factor=100, diag=None)
一般我们只需要使用前两个参数，分别是写有方程的函数，和初始值。
详细介绍
例：
$$\{\begin{array}{c}2\ast x-y=2\\ x^2+y^2=8\end{array}$$
函数图像：

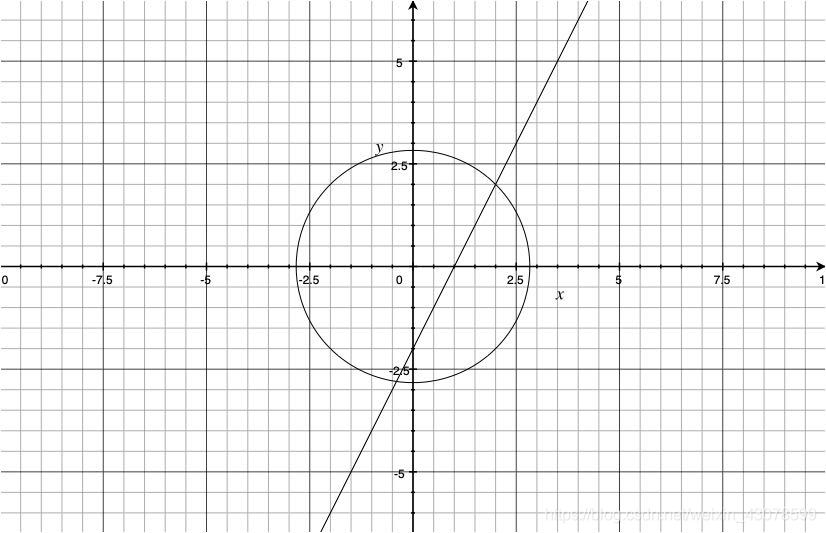
代码：

from scipy.optimize import fsolve
def func(i):
    x, y, = i[0], i[1]
    return [
            2 * x - y - 2,
            x ** 2 + y ** 2 -8
            ]
r = fsolve(func,[0, 0])
print (r)

由于fsolve采用迭代的数值算法，只输出结果（-0.4，-2.8），但由函数图像可知有两解。所以初值的设置尤为重要。

三·SymPy寻找全部结果

from sympy import solve,Symbol
x = Symbol('x')
y = Symbol('y')
r = solve([2 * x - y - 2,x ** 2 + y ** 2 -8],[x, y])
print(r)

返回结果： [(-2/5, -14/5), (2, 2)]