前言
- 掌握使用PyTorch构建LSTM模型的方法
- 掌握使用LSTM生成MIDI音乐的方法
主要内容
- 如何用神经网络做序列生成?
- RNN 与 LSTM 的工作原理
- RNN 是如何记忆 Pattern 的?
- MIDI 音乐的原理
- 如何用LSTM 作曲


一、序列生成问题解决方法
- 将生成问题转化成一个预测问题
- 完成自举过程: 给定一个种子,不断用已经生成的数据预测下一个数据
例子:


二、RNN的引入

h
t
=
σ
(
W
X
h
X
t
+
W
h
h
h
t
−
1
)
Y
t
=
σ
(
W
h
Y
h
t
)
\begin{array}{l} h_{t}=\sigma\left(W_{X h} X_{t}+W_{h h} h_{t-1}\right) \\ Y_{t}=\sigma\left(W_{h Y} h_{t}\right) \end{array}
ht=σ(WXhXt+Whhht−1)Yt=σ(WhYht)
公式讲解:
隐藏层运算:
h
t
h_{t}
ht和上一时刻的
h
t
−
1
h_{t-1}
ht−1以及输入的
X
t
X_{t}
Xt,权重
W
X
h
W_{X h}
WXh有关
输出层:
h
t
h_{t}
ht乘上权重矩阵
W
h
Y
W_{h Y}
WhY再经过一个非线性的激活函数
σ
\sigma
σ和前馈神经网络类似;
人类视角:记忆/计数能力
3:代表开始
2:代表结束
0/1:代表rnn学习的model
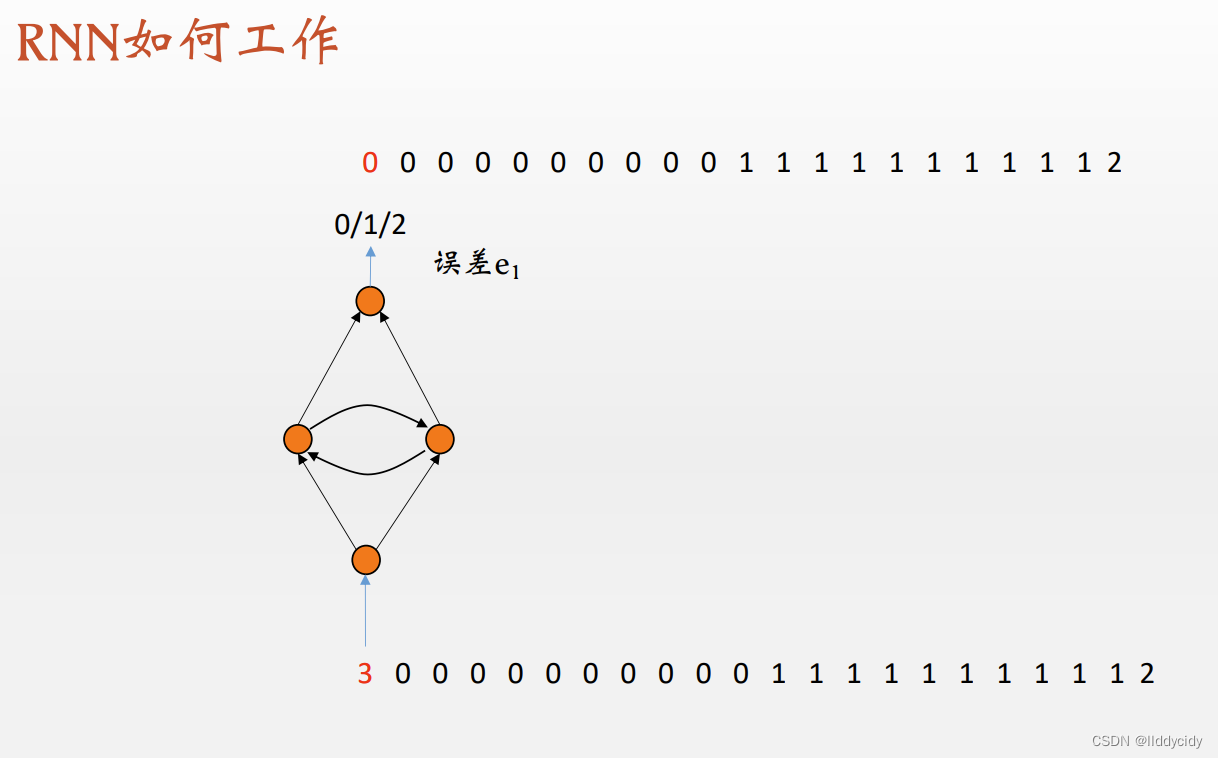

输入为one-hot编码
输出为多分类

损失函数:交叉熵




我们发现测试效果中,我们的
p
a
t
t
e
r
n
pattern
pattern—"
0
n
1
n
0^{n} 1^{n}
0n1n"并没有很好的预测
其实这是必然的
但是我们的结束字符是工作很好的

采样方式如上


训练好的网络的权重是固定的,那么我们读出相关的权重就可以画出相应的输出层
y
=
σ
(
w
h
2
(
h
1
)
+
w
h
2
(
h
2
)
)
y=\sigma\left(w_{h_{2}} (h_{1})+w_{h_{2}}(h_{2})\right)
y=σ(wh2(h1)+wh2(h2))

序列变长时:(反复横跳)

更长的时候,开始震荡

P Rodriguez et al., A Recurrent Neural Network that Learns toCount, Connection Science, Vol.11,No1,1999:5-40
RNN弊端:
RNN的局限:长期依赖(Long-TermDependencies)问题
在这个间隔不断增大时,RNN会丧失学习到连接如此远的信息的能力;
换句话说, RNN会受到短时记忆的影响。如果一条序列足够长,那它们将很难将信息从较早的时间步传送到后面的时间步。
因此,如果你正在尝试处理一段文本进行预测,RNN可能从一开始就会遗漏重要信息。
在反向传播期间(反向传播是一个很重要的核心议题,本质是通过不断缩小误差去更新权值,从而不断去修正拟合的函数),RNN会面临梯度消失的问题。
因为梯度是用于更新神经网络的权重值(新的权值 = 旧权值 - 学习率*梯度),梯度会随着时间的推移不断下降减少,而当梯度值变得非常小时,就不会继续学习。
即:RNN处理不了距离长的问题

三、Long Short Term Memory(LSTM)
与rnn进行对比
构成


h
t
+
1
=
o
t
∗
tanh
(
c
t
)
c
t
+
1
=
f
t
∗
c
t
+
i
t
∗
g
t
g
t
=
tanh
(
W
i
g
x
t
+
W
h
c
h
t
+
b
g
)
\begin{array}{c} h_{t+1}=o_{t} * \tanh \left(c_{t}\right) \\ c_{t+1}=f_{t} * c_{t}+i_{t} * g_{t} \\ g_{t}=\tanh \left(W_{i g} x_{t}+W_{h c} h_{t}+b_{g}\right) \end{array}
ht+1=ot∗tanh(ct)ct+1=ft∗ct+it∗gtgt=tanh(Wigxt+Whcht+bg)
i
t
+
1
=
σ
(
W
i
i
x
t
+
W
h
i
h
t
+
b
i
)
f
t
+
1
=
σ
(
W
i
f
x
t
+
W
h
f
h
t
+
b
f
)
o
t
+
1
=
σ
(
W
i
o
x
t
+
W
h
o
h
t
+
b
o
)
\begin{aligned} i_{t+1} & =\sigma\left(W_{i i} x_{t}+W_{h i} h_{t}+b_{i}\right) \\ f_{t+1} & =\sigma\left(W_{i f} x_{t}+W_{h f} h_{t}+b_{f}\right) \\ o_{t+1} & =\sigma\left(W_{i o} x_{t}+W_{h o} h_{t}+b_{o}\right) \end{aligned}
it+1ft+1ot+1=σ(Wiixt+Whiht+bi)=σ(Wifxt+Whfht+bf)=σ(Wioxt+Whoht+bo)
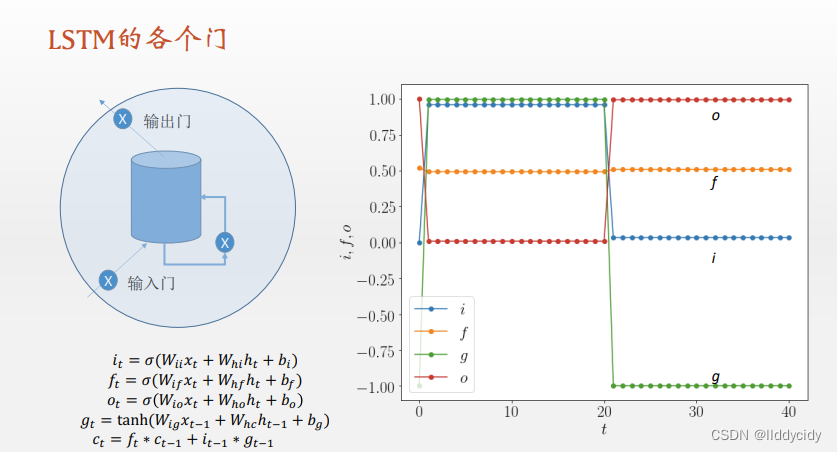
LSTM一个细胞的结构:

遗忘门
f
t
f_{t}
ft:
在LSTM模型中,第一步是决定我们从“细胞”中丢弃什么信息,这个操作由一个忘记门层来完成。该层读取当前输入x和前神经元信息h,由
f
t
f_{t}
ft来决定丢弃的信息。输出结果1表示“完全保留”,0 表示“完全舍弃”。

输入门(更新门
i
t
i_{t}
it)
第二步是确定细胞状态所存放的新信息,这一步由两层组成。sigmoid层作为“输入门层”,决定我们将要更新的值i;tanh层来创建一个新的候选值向量
C
~
t
\tilde{C}_{t}
C~t
加入到状态中。在语言模型的例子中,我们希望增加新的主语到细胞状态中,来替代旧的需要忘记的主语。
第三步就是更新旧细胞的状态,将
C
t
−
1
C_{t-1}
Ct−1更新为
C
t
C_{t}
Ct。我们把旧状态与
f
t
f_{t}
ft相乘,丢弃掉我们确定需要丢弃的信息。接着加上
i
t
∗
C
~
t
i_{t} * \tilde{C}_{t}
it∗C~t。这就是新的候选值,根据我们决定更新每个状态的程度进行变化。在语言模型的例子中,这就是我们实际根据前面确定的目标,丢弃旧代词的信息并添加新的信息的地方。
最后一步就是确定输出了,这个输出将会基于我们的细胞状态,但是也是一个过滤后的版本。首先,我们运行一个 sigmoid 层来确定细胞状态的哪个部分将输出出去。接着,我们把细胞状态通过 tanh 进行处理(得到一个在 -1 到 1 之间的值)并将它和 sigmoid 门的输出相乘,最终我们仅仅会输出我们确定输出的那部分。在语言模型的例子中,因为语境中有一个代词,可能需要输出与之相关的信息。例如,输出判断是一个动词,那么我们需要根据代词是单数还是负数,进行动词的词形变化。



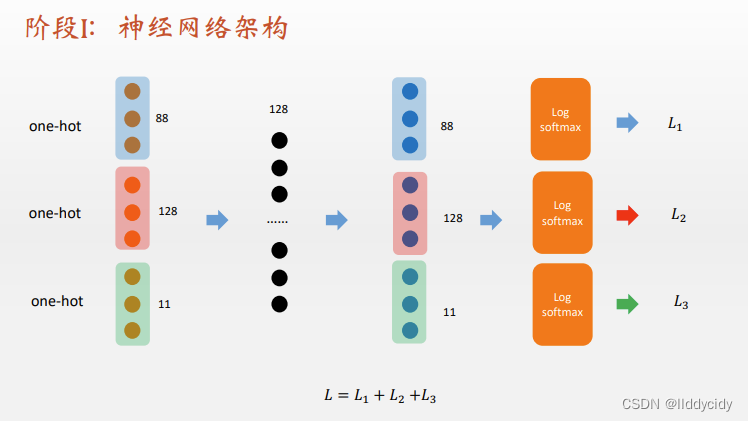
4、序列生成音乐



本文引用:
代码
参考文献:
Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting下载地址








 本文介绍了如何使用PyTorch构建LSTM模型来解决序列生成问题,特别是针对音乐创作。文章讨论了RNN的工作原理,包括其记忆模式和存在的长期依赖问题,以及LSTM如何通过其结构克服这些问题。此外,还提到了使用LSTM进行MIDI音乐生成的方法。
本文介绍了如何使用PyTorch构建LSTM模型来解决序列生成问题,特别是针对音乐创作。文章讨论了RNN的工作原理,包括其记忆模式和存在的长期依赖问题,以及LSTM如何通过其结构克服这些问题。此外,还提到了使用LSTM进行MIDI音乐生成的方法。





















 1033
1033

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








