【李航-统计学习方法】第五章- 决策树-1

本章概述

1、 决策树基本概念
2、通过ID3和C4.5介绍
* 特征的选择、决策树的生成
* 决策树的修建
3、CART算法

5.1 决策树模型与学习

5.1.1决策树模型

用决策树分类，从根结点开始，对实例的某一特征进行测试，根据测试结果，将实例分配到其子结点；这时，每一个子结点对应着该特征的一个取值。如此递归地对实例进行测试并分配，直至达到叶结点。最后将实例分到叶结点的类中。
圆代表内部结点，方框代表叶子结点。（这里表示方式因人而异，如下图就是圆代表叶子结点，方框代表内部结点）

5.1.2 决策树与if-then规则

5.1.3 决策树与条件概率分布

决策树表示给定条件下类的条件概率分布。
这一条件概率分布定义在特定空间的一个划分（partition）。将特征空间划分未互不相交的单元（cell）或区域（region），并在每个单元定义一个类的概率分布就构成了一个条件概率分布。
决策树的一条路径对应于划分中的一个单元。
决策树所表示的条件概率分布由各个单元给定条件下类的条件概率分布组成。
假设$X$为表示特征的随机变量，$Y$为表示类的随机变量，那么这个条件概率分布就可以表示为$p(Y|X)$。

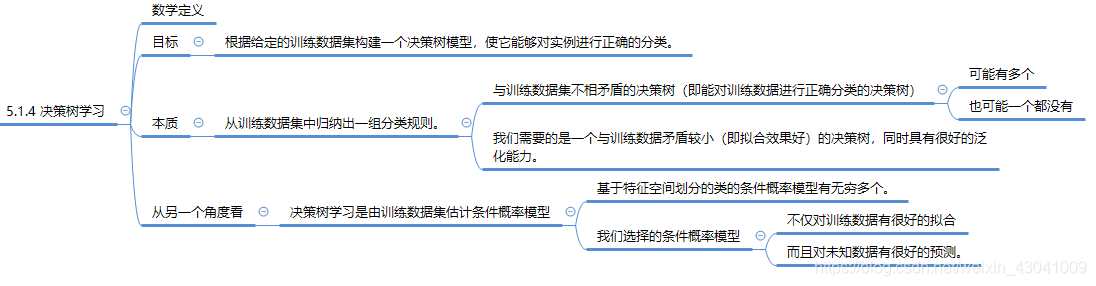
5.1.4 决策树学习

假定给定训练数据集
$$D=(x_1,y_1),(x_2,y_2),...,(x_N,y_N)$$
其中，$x_i=(x_i^1,x_i^2,...,x_i^n{)}^T$为输入实例（特征向量），n为特征个数，$y_i\in 1,2,....k$为类标记，i=1,2,…,N,N为样本容量。

损失函数用于表示目标：即既有良好的训练集拟合能力，又有对未知数据的很好的预测。
决策树的损失函数通常是正则化的极大似然函数，故目标是以损失函数为目标函数的最小化。
当损失函数确定后，学习问题就变为在损失函数意义下，选择最优决策树的问题。因为从所有可能的决策树中选取最优决策树是NP完全问题（Non-deterministic Polynomial Complete的问题，即多项式复杂程度的非确定性问题），所以现实中决策树学习算法通常采用启发式方法，近似求解这一最优化问题。这样得到的决策树是次最优的（sub-optimal）的。
决策树学习的算法通常是一个递归地选择最优特征，并根据该特征对训练数据进行分割，使得对各个子数据集有一个最好的分类的过程。这一过程对应着对特征空间的划分，也对应着决策树的构建。如此递归下去，直至所有训练数据子集被基本正确分类，或者没有合适的特征为止。最后每个子集都被分到叶结点上，即都有了明确的类。这就生成了一颗决策树。

以上方法生成的决策树可能对训练数据有很好的分类能力，但对未知的测试数据却未必有很好的分类能力，即可能发生过拟合现象（模型很细以及复杂（树很深），导致模型对训练集上表现很好）。我们需要对已生成的树自下而上进行剪枝，将树变得更简单，从而使它具有更好的泛化能力。具体来说，就是去掉过于细分的叶结点，使其回退到父节点，甚至更高的结点，然后将父节点或更高的结点改为新的叶结点。

为什么说决策树包含特征选择呢?
因为决策树会优先选择对训练数据有足够分类能力的特征。（比如下不下雨对是否出去玩具有决定作用。）

总结：
决策树学习算法包含特征选择、决策树生成与决策树的剪枝过程。
由于决策树表示一个条件概率分布，所以深浅不同的决策树对应着不同复杂度的概率模型。**决策树的生成对应于模型的局部选择，决策树的剪枝对应于模型的全局选择。**决策树的生成只考虑局部最优，相对地，决策树的剪枝则考虑全局最优。

Ref.

[1] 李航. 统计学习方法[M],清华大学出版社.