算法金 | 10 大必知的人工智能算法-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_43038668/article/details/139392418

大侠幸会，在下全网同名[算法金] 0 基础转 AI 上岸，多个算法赛 Top [日更万日，让更多人享受智能乐趣]

武林秘籍辣么多，怎么修得过来

在人工智能的浩瀚领域中，各式算法犹如武林中的各派秘籍，引领着探索者们穿梭于智能化的世界。本文将作为基础指南，带你一探这些算法的奥秘，从统计机器学习到深度学习，一步步揭开人工智能的面纱。必知必会 10 大人工智能算法：线性回归、逻辑回归、决策树、朴素贝叶斯、支持向量机（SVM）、集成学习、K近邻算法、K-means算法、主成分分析（PCA）、神经网络万字长文，建议先收藏再品

「1 线性回归」：打开人工智能的第一扇门 1.1 概念：模型简介与应用场景

定义：
线性回归是一种用于预测与分析的统计学方法，旨在研究两个或多个变量之间线性关系的强度。
在简单线性回归中，我们关注的是一个自变量和一个因变量之间的线性关系；而在多元线性回归中，会涉及两个或两个以上的自变量。
应用场景：
广泛应用于经济学、生物统计、环境科学等领域，比如预测房价、股票价格、气温变化等。

1.2 原理：最小二乘法

基本思想：
线性回归通过最小化误差的平方和来寻找数据集中最佳拟合直线。
简单来说，就是尽量让所有的数据点到直线的距离（即误差）的总和达到最小。
一图胜千言：

1.3 优缺点分析

优点：
简单直观：模型易于理解和解释，是进入数据科学领域的良好起点。
计算效率高：线性回归模型可以快速训练，对于初学者和处理大规模数据集尤为友好。
广泛的应用场景：从金融预测到自然科学研究，线性回归都能发挥作用。
缺点：
对异常值敏感：异常值可以极大地影响回归线和最终预测结果。
线性假设的局限性：当实际数据之间的关系不是线性时，线性回归的效果会大打折扣。

1.4 代码实战

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# 设置matplotlib支持中文显示
plt.rcParams['font.sans-serif'] = ['SimHei'] # 设置中文显示
plt.rcParams['axes.unicode_minus'] = False # 正确显示负号

# 创建武侠世界中的功力（X）与成名年数（y）的数据
X = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10]).reshape(-1, 1) # 功力等级
y = np.array([2, 3, 3.5, 5, 6, 7.5, 8, 9, 10.5, 11]) # 成名年数

# 使用线性回归模型
model = LinearRegression()
model.fit(X, y) # 训练模型

# 预测功力等级对应的成名年数
X_predict = np.array([11, 12, 13]).reshape(-1, 1) # 新的功力等级
y_predict = model.predict(X_predict) # 进行预测

# 绘制功力与成名年数的关系
plt.scatter(X, y, color='red', label='实际成名年数') # 原始数据点
plt.plot(X, model.predict(X), color='blue', label='功力成名模型') # 拟合的直线
plt.scatter(X_predict, y_predict, color='green', label='预测成名年数') # 预测点
plt.xlabel('功力等级')
plt.ylabel('成名年数')
plt.title('武侠世界的功力与成名年数关系')
plt.legend()
plt.show()

线性回归作为人工智能领域的基石之一，不仅让我们了解到数据之间复杂关系的线性表达，还为我们提供了解决实际问题的有效工具。通过学习和应用线性回归，我们能够更深入地探索数据科学和机器学习的奥秘。

「 2 逻辑回归」：从线性到分类的桥梁

2.1 概念：与线性回归的联系与区别

定义：
逻辑回归是一种广泛用于分类问题的统计方法，尤其擅长处理二分类问题。
它通过使用逻辑函数（通常是Sigmoid函数）来预测事件发生的概率。
联系与区别：
与线性回归类似，逻辑回归也是估计变量之间的关系。
主要区别在于，线性回归直接预测数值，而逻辑回归则预测类别（如红或蓝）。

2.2 原理：Sigmoid 函数

Sigmoid 函数：逻辑回归中使用的Sigmoid函数能将任意实数值映射到 (0, 1) 区间，便于解释为概率。
一图胜千言：

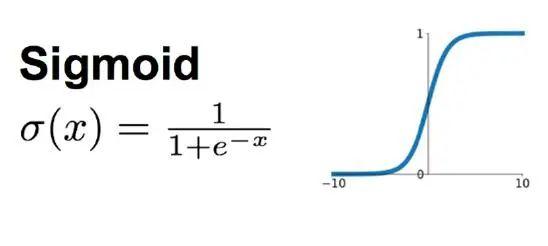
2.3 应用场景：二分类问题

医疗领域：预测疾病发生的概率，如糖尿病或心脏病。
金融行业：信用评分，预测客户违约的可能性。
营销策略：预测用户是否会对特定的广告点击或购买产品。 2.4 优缺点分析
优点：
输出可解释性强：逻辑回归的输出可以直接解释为概率，便于理解和解释。
简单高效：适用于小至中等数据集，训练速度快。
易于实现：算法简洁，易于编程实现。
缺点：
处理非线性问题能力弱：当特征与标签之间的关系非线性时，逻辑回归的表现不如某些其他算法。
对多类别问题支持不足：虽然可以通过策略如一对多（OvR）来扩展到多分类问题，但效果和效率可能不如专门设计的算法。

from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_classification
import matplotlib.pyplot as plt
import numpy as np

# 生成模拟的武侠世界功力和内功心法数据集
X, y = make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=42)

# 创建逻辑回归模型对象
lr = LogisticRegression()

# 训练模型
lr.fit(X, y)

# 定义决策边界绘制函数
def plot_decision_boundary(X, y, model):
    # 设置最小和最大值，以及增量
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.mes